מכונת בולצמן

הצגה גרפית לדוגמה למכונת בולצמן. כל קודקוד בגרף מייצג נוירון וכל קשת מייצגת קשר. בדוגמה הספציפית הזו יש 4 נוירונים בשכבה הגלויה ו-3 נוירונים בשכבה הנסתרת. זו אינה רשת בולצמן מוגבלת.

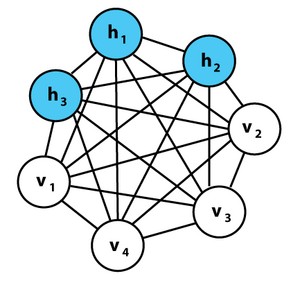
מכונת בולצמן היא רשת נוירונים מבוססת הסתברות והיא גם שדה אקראי של מרקוב. המודל של הרשת נלקח מהמכניקה הסטטיסטית, ובפרט הוא מבוסס על מודל הזכוכית-ספין. השימוש העיקרי ברשת הוא לצורך פיתוח אלגוריתמים ללמידת מכונה. מכונת בולצמן שייכת לסוג רשתות הנקראות "מבוססות אנרגיה", כלומר היא מבוססת על תיאור אנרגטי של מערכת פיזיקלית.

אופן פעולת הרשת מסקרן בעיקר בגלל הקשר שלהם לתהליכים פיזיקליים פשוטים, בעוד שמכונות בולצמן עם קישוריות בלתי מוגבלת לא הוכחה כיעילה מספיק לפתרון בעיות מעשיות. אולם, אם הקישוריות של הרשת מוגבלת בצורה בנכונה (כפי שיוסבר בהמשך), ניתן להפוך את הרשת ליעילה מספיק עבור פתרון של בעיות מעשיות של למידת מכונה והסקה.

שמה של הרשת נקרא על שם התפלגות בולצמן, אשר שימושית בבעיות רבות במכניקה סטטיסטית.

המודל של הרשת הומצא בשנת 1985, על ידי ג'פרי היינטון, שהיה אז פרופסור באוניברסיטת קרנג'י מלון, וטרי סיינובסקי, אז פרופסור באוניברסיטת ג'ונס הופקינס.

רשת הופ'פילד ומצב שיווי משקל

מכונת בולצמן היא מקרה פרטי של רשת הופ'פילד ובפרט של רשת הופ'פילד סטטיסטית. נזכיר בקצרה את התכונות של רשת הופ'פילד על מנת לתאר את מכונת בולצמן ואת הקשר שלה למושג האנרגיה.

רשת הופ'פילד בינארית, המבוססת על התיאור הפיזיקלי של ספין-זכוכית יכולה להיות מתוארת על ידי קודקודים (ספינים) אשר יש להם קשר אנרגטי זה עם זה, כאשר האנרגיה של כל המערכת נקבעת על פי ערכם של הנוירונים שבה.

נוכל לתאר זאת על ידי שדה שמרגיש הנוירון, שנקבע על פי מצבם של שאר הנוירונים במערכת, כאשר ערכו נקבע כך:

$y_{i}=\theta (\sum _{j\neq i}w_{ji}y_{j}+b_{i})$

כאשר $\theta$ היא פשוט פונקציית הסימן, כלומר ערכה הוא 1 אם סימן הארגומנט שמוכנס אליה חיובי וערכה הוא $-1$ אחרת.

ניתן לראות זאת מבחינה פיזיקלית כספין שמסתדר בהתאם לכיוון השדה שפועל עליו.

האנרגיה של המערכת תתואר כ:

$E=-\sum _{i,j<i}w_{ij}y_{i}y_{j}-\sum _{i}b_{i}y_{i}$

הרחבה לרשת הופ'פילד היא רשת הופ'פילד שאינה דטרמיניסית אלא סטטיסטית (כלומר ערכי הספיני שבה אינם נקבעים באופן חד ערכי בהתאם לכיוון השדה שפועל עליהם אלא באופן הסתברותי).

כעת נתאר זאת כך:

$z_{i}={1 \over T}\sum _{j\neq i}w_{ji}y_{j}+b_{i}$

$P(y_{i}=1)=\sigma (z_{i})$

$P(y_{i}=0)=1-\sigma (z_{i})$

כאשר $\sigma$ היא פונקציית הסיגמואיד המוגדרת כ: $\sigma (x)={1 \over {1+e^{-x}}}$. T מתאר את "טמפרטורת המערכת" וקביעה שלו כערכים מסוימים שימושית לצורך נתינת תכונות מסוימות למערכת.

נשים לב כי פונקציית הסיגמואיד מחזירה ערכים שבין 0 ל-1 כמצופה מפונקציית הסתברות.

נדגיש כי גם ברשת הסטטיסטית מדובר על רשת בינארית, כלומר כל נוירון יכול לקבל ערך של 0 או 1, אבל הערך לא נקבע באופן חד ערכי על פי ערכי הנוירונים האחרים אלא יש לו הסתברות להיות בכל אחד מהמצבים.

כעת נכנס לתמונה מושג שיווי המשקל. אם נאתחל את המערכת עם ערכים כלשהם וניתן לה להשתנות במשך מספיק זמן, כלומר ניתן לערכי הנוירונים שבה להשתנות בהתאם לשדה שהם מרגישים, בסופו של דבר המערכת תגיע למצב שיווי משקל, כלומר למצב שבו ערך האנרגיה שהגדרנו הוא מינימלי, זאת בדומה למערכות פיזיקליות השואפות להגיע למצב שבו האנרגיה הפוטנציאלית שלהם מינימלית.

נשים לב כי לפונקציית האנרגיה שהגדרנו יכולים להיות נקודות מינימום מקומי שאינן מינימום גלובלי של פונקציית האנרגיה. המטרה שלנו היא לגרום למערכת להגיע אל אחת מנקודות המינימום של האנרגיה בתהליך שמכונה "אימון" של הרשת ועל כך יורחב בהמשך.

מבנה

הצגה גרפית של מכונת בולצמן. כל קשת בגרף מציינת קשר בין קודקודים כאשר w הוא המשקל המקשר בין הקודקודים הנ"ל. זוהי מכונת בולצמן לא מוגבלת.

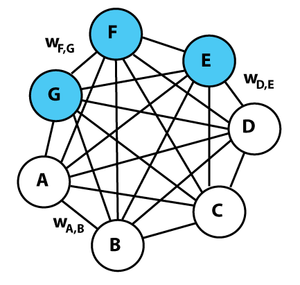
בדומה לרשת הופפילד, מכונת בולצמן היא רשת של מצבים (ניתנים לייצוג על ידי קודקודים בגרף) שמיוצגים על ידי ערכים בינאריים, שאת המצב שלה אפשר להגדיר על ידי "אנרגיה". האנרגיה נתונה על ידי הנוסחא הבאה:

$E=-(\sum _{i<j}w_{i,j}s_{i}s_{j}+\sum _{i}\theta _{i}s_{i})$

כאשר:

$w_{i,j}$ הוא הקשר בין המצב הi למצב הj (בצורה אינטואיטיבית, אם נייצג את הרשת כגרף, אז w יהיה הערך של הקשת בין קודקוד i לקודקוד j, או "עוצמת הקשר" ביניהם).

$s_{i}$ הוא המצב הi, שיכול לקבל את הערך 1 או 0.

$\theta _{i}$ הוא ערך ההטיה של האנרגיה.

נשים לב כי הסכימה היא על $i<j$ על מנת למנוע כפילות באנרגיה. כלומר, עבור כל קודקודים i,j יש לסכום רק פעם אחת.

ההסתברות למצב יחיד

נראה את הפיתוח של הנוסחא להסתברות של מצב יחיד שמבוססת על התפלגות בולצמן:

נניח שאנו לוקחים את המערכת כאשר היא נתונה עם אנרגיה ספציפית, ומשנים את ערכו של אחד המצבים ("מכבים" אותו). על סמך הנוסחא שכתבנו לאנרגיה של המערכת נוכל לכתוב את הפרש האנרגיה כתוצאה מהשינוי:

$\Delta E_{i}=E_{i=off}-E_{i=on}=\sum _{j<i}w_{ij}s_{j}+\theta _{i}$

אנו יודעים מהתפלגות בולצמן כי הסיכוי כי מערכת תסתדר בקונפיגורציה מסוימת פרופוריונצלי ל$e^{-{\epsilon _{i} \over kT}}$

כאשר $\epsilon _{i}$ היא האנרגיה של הקונפיגורציה. לכן נוכל להסיק כי:

$\Delta E_{i}=-k_{B}Tln(P_{i=off})-(-k_{B}Tln(P_{i=on}))$

כאשר $k_{B}$ הוא קבוע בוצלמן וT היא ה"טמפרטורה" של המערכת.

מכיוון שאנו יודעים כיסכום הסתברויות חייב להסתכם ל-1 נקבל:

${{\Delta E_{i}} \over T}=ln(P_{i=on})-ln(P_{i=off})$

${{\Delta E_{i}} \over T}=ln(P_{i=on})-ln(1-P_{i=on})$

${{\Delta E_{i}} \over T}=ln({(p_{i=on}) \over (1-p_{i=on})})$

$-{\Delta E_{i} \over T}=ln({{1 \over P_{i=on}}-1})$

$exp({-\Delta E_{i} \over T})={1 \over P_{i=on}}-1$

כלומר ההסתברות כי המצב ה-i הוא 1 נתונה על ידי:

$P_{i=on}={1 \over {1+exp({-\Delta E_{i} \over T})}}$

שהיא למעשה פונקציית הסיגמואיד.

מכונת בולצמן מוגבלת

כפי שהזכרנו, מכונת בולצמן לא הוכחה כיעילה למימוש בעיות מעשיות, אולם שימוש בגרסה שלה המכונה 'רשת בולצמן מוגבלת' (Restricted Boltzmann machine- RBM) הוא דווקא שימושי למגוון בעיות.

האלגוריתם מבוסס על רשת נוירונים, אשר מתוארת בתרשים לעיל. כל עיגול מתאר "נוירון", שהוא פשוט 'מקום' בו מתבצעים חישובים שעל פיהם הוא מחליט אם להעביר את הקלט או לא. שם נוסף לנוירון הוא צומת. האלגוריתם מורכב משתי שכבות, שנקראות השכבה הגלויה והשכבה הנסתרת. כפי שהסברנו, כל אחד מהצמתים מקושר לכל צומת שבשכבה הנגדית, אבל אף אחד מצמתים אינו מקושר לצומת שנמצא בשכבה שלו.

ניתן להסביר את היתרון שבמכונת בולצמן מוגבלת על פני מכונת בולצמן רגילה כך: במכונת בולצמן רגילה ערכו של כל נוירון תלוי בערכם של כל הנוירונים האחרים, ואם נרצה לשנות את ערכם של הנוירונים ברשת הדבר ייקח זמן רב, שכן בכל איטרציה רק ערכו של נוירון אחד יוכל להשתנות (הנוירונים בכל שכבה תלויים זה בזה). לעומת זאת, במכונת בולצמן מוגבלת נוכל לשנות את ערכם של הנוירונים בשכבה מסוימת, למשל השכבה הנסתרת בבת אחת, בהתחשב בערכם של הנוירונים בשכבה הגלויה בלבד.

השלב הראשון של האלגוריתם - מעבר מהשכבה הגלויה לשכבה הנסתרת

בתחילת התהליך שנקרא תהליך הלמידה של האלגוריתם, מוזן לכל אחד מהצמתים בשכבה הגלויה קלט. לדוגמה- הקלט הוא תמונה בצבעי שחור-לבן. תמונה כזו מתוארת על ידי אוסף מספרים (נניח 720) שכל אחד מהם מציין את 'מידת הצביעה' של נקודה מסוימת (פיקסל) בתמונה, כאשר '1' יתאר נקודה שחורה, '0' יתאר נקודה לבנה, וכל מספר אחר בתחום שבין 0 ל-1 יתאר צבע ביניים אפור כלשהו. בדוגמה זו הקלט יהיה פשוט רצף של 720 מספרים (וקטור) אשר כל אחד מהם מוזן אל אחד מ-720 צמתי הקלט, שהם 720 הצמתים שבשכבה הגלויה של האלגוריתם. אנו נתמקד במקרה של קלט בינארי, כלומר שיכול לקבל את הערכים 1 או 0 בלבד.

כעת, הנתונים מהשכבה הגלויה 'זורמים' אל השכבה הנסתרת, כאשר כל קודקוד בשכבה הנסתרת מושפע מכל אחד מהקודקודים שמקושרים אליו בצורה הבאה: ראשית מוכפל כל אחד מהקלטים ב'משקל' (weight). את תוצאת כל הקלטים המוכפלים במשקל שלהם סוכמים יחד עם מספר נוסף המכונה 'הטיה' (bias). הסכום הנ"ל נכנס לתוך פונקציה הנקראת 'פונקציית הפעלה' (activation function) שתוצאה תהיה ההסתברות כי הערך של הקודקוד יהיה 1. תהליך זה מתבצע עבור כל אחד מהצמתים בשכבה הנסתרת. בהערת אגב נעיר כי מהותו של השימוש בפונקציית ההפעלה הוא שהסכום המתקבל יכול להיות גדול מ-1, אולם אנחנו מעוניינים בערכים של מספרים בין 0 ל-1, זאת משום שהערך של פונקציית הפעולה יציין את הסיכוי­ כי האות יועבר (כלומר הנוירון יקבל את הערך 1 ולא 0). במקרים רבים נעשה שימוש בפונקציית הסיגמואיד שתוארה לעיל, כך שעבור כל ערך ממשי הפוקציה מחזירה מספר בין 0 ל-1.

נשים לב כי לכל חץ בגרף יש משקל w ייחודי. עבור 20 צמתים בשכבה הגלויה ו-10 צמתים בשכבה הנסתרת, למשל, יהיו $20*10=200$ ערכי w.

את הצעד הראשון אפשר לתאר בצורה מטריצית כך:

$h^{(1)}=\sigma ({v^{(0)T}}w+b)$

השלב השני של האלגוריתם- מעבר מהשכבה הנסתרת לשכבה הגלויה

כאשר $v^{(0)}$ הוא וקטור הקלטים, $w$ היא מטריצת המשקלים, ו-$b$ היא מטריצת ההטיות.

בשלב הבא הרשת 'הופכת כיוונים'. כלומר ערכי הצמתים בשכבה הנסתרת יהיו הקלטים והם אלה שיחלחלו אל השכבה הגלויה. כלומר עבור צומת בשכבה הגלויה נסכום את כל ערכי הצמתים שבשכבה מוכפלים במשקל w המתאים (נשים לב שאלו אותם משקלים מהשלב הקודם) יחד עם ערך ההטייה b המתאים והסכום הנ"ל (לאחר מעבר בפונקציית הפעולה יקבעו את הערך של הצומת בשכבה הגלויה. נשים לב כי ערכי הb האלה שונים מערכי הb הקודמים. למעשה לכל צומת בגרף (בשכבה הגלויה ובשכבה הנסתרת יש ערך b משלה.

את שלב זה נתאר כך:

$v^{(1)}=\sigma (h^{(1)}w^{T}+b)$

כעת מגיע השלב המכונה "שלב הלמידה" של האלגוריתם.

נגדיר כי אנו מצפים כי $v^{(1)}$ יהווה "שחזור" של הקלט המקורי $v^{(0)}$ שהתקבל מלכתחילה. אם זו הציפייה שלנו, נוכל לקרוא להפרש ביניהם, $v^{(0)}-v^{(1)}$ כ"שגיאה" של השחזור, כאשר המטרה שלנו היא אימון האלגוריתם על מנת למזער ערך זה ככל הניתן, זאת בעזרת הרצה של שני השלבים שתארנו מספר פעמים ושינוי של ערכי המשקלים w.

ננסה לתאר את התהליך בצורה אינטואיטיבית ככל האפשר מבלי להיכנס לנוסחאות המלאות.

אנו בעצם מנסים למצוא בכל איטרציה את ה'גרדיאנט' של ערכי המשקלים. כלומר את השינויים הנדרשים על מנת שערך השגיאה שהוגדר יהיה קטן ככל האפשר.

הגרדיאנט הוא אופרטור המהווה מעין הרחבה של מושג הנגזרת. בהינתן פונקציה של שני משתנים (למשל $f(x,y)=x^{2}+5y$ ), ערכו של הגרדיאנט בנקודה ספציפי ייתן לנו את הכיוון בו הפונקציה משתנה הכי הרבה, את הכיוון בו השיפוע תלול ביותר. באנלוגיה לגרדיאנט, אנו נרצה למצוא גם כאן את השינוי שיש לבצע בכל אחד מהמשקלים שלנו על למזער את השגיאה מהר ככל הניתן, או את "הכיוון במרחב המשקלים אליו יש ללכת" כדי לעשות זאת.

נזכיר כעת כי ה-RBM מבוסס על העובדה כי אין קשרים בין קודקודים שנמצאים באותה שכבה בגרף, ולכן ההסתברויות של קודקודים באותה שכבה בלתי תלויות, ונוכל להשתמש בנוסחאת ההתפלגות המותנית:

$P(v|h)=\prod _{i=1}^{m}P(v_{i}|h)$

ועבור המעבר ההפוך (כלומר כאשר נרצה לחשב את ערכי הקודקודים v על סמך הקודקודים h):

$P(h|v)=\prod _{i=1}^{n}P(h_{j}|v)$

כעת, את ערכה של פונקציית הפעולה הספציפית (המציינת, כאמור, את הסיכוי כי הנוירון "יידלק"), נוכל לחשב כך:

$P(h_{j}=1|v)=\sigma (b_{j}+\sum _{i=1}^{m}w_{i,j}v_{i})$

$P(v_{i}=1|v)=\sigma (a_{j}+\sum _{j=1}^{n}w_{i,j}h_{i})$

בשונה מרשתות דטרמיניסטיות, האלגוריתם לא מנסה למצוא כאן ערך ספציפי אלא את מה הסיכוי שההתפלגות שקיבלנו נוצרה כתוצאה מהתפלגות קודמת. כלומר הוא למעשה מנסה לגלות מספר רב של ערכים בו זמנית. תהליך זה מכונה למידה גנרטיבית.

נניח כי יש לנו שתי התפלגויות נורמליות, אחת מסמנת את התפלגות נתוני הקלט ומסומנת כ-$p(x)$ והשנייה מסמנת את נתוני הפלט ומסומנת כ$q(x)$. ההפרש בין הפונקציות הנ"ל הוא השגיאה שלנו, אותה אנו מנסים. כלומר, מבחינה רעיונית אנו מנסים "לקרב" את הגרפים p,q זה אל זה.

רעיון זה מיוצג על ידי מונח שנקרא סטיית קולבק-לייבלר (KL). הסטייה של KL מודדת את האזורים הלא חופפים תחת שני הגרפים ואלגוריתם האופטימיזציה של ה-RBM מנסה למזער את ההפרש על ידי שינוי המשקלים.

נראה בצורה מעט יותר ריגורוזית את תהליך מציאת הגרדיאנט של המשקלים:

כאמור, המודל של RBM מבוסס על ערכים- בינאריים (0 או 1) של הקודקודים (הקודקודים הנסתרים יסמנו ב-h והקודקודים הגלויים יסומנו ב-v) ומכיל את מטריצת המשקלים (כל ערכי ה-w המקשרים בין קודקודים בגרף) וערכי ההטיות (כאשר הטיה השייכת לקודקוד בשכבה הנסתרת תסומן באות b והטיה השייכת לקדקוד בשכבה הגלויה תסומן ב-a).

כעת עבור קונפיגורציה (אופן סידור כלשהו) של הגרף, נגדיר את ה"אנרגיה" של המערכת כך:

$-\sum _{i}a_{i}v_{i}-\sum _{j}b_{j}h_{j}-\sum _{i}\sum _{j}v_{i}w_{i,j}h_{j}$

בדומה למודל הפיזיקלי, הסיכוי לקבלת קונפיגורציה כלשהי של ערכי v,h תהיה:

$P(v,h)={1 \over Z}e^{-E(v,h)}$

כאשר Z היא פונקציית החלוקה ומטרתה בסך הכל נירמול של ההסתברויות כך שההתפלגות של סך ההסתברויות תהיה 1, כלומר:

$Z=\sum _{v}\sum _{h}e^{-E(v,h)}$

כעת, נניח כי אנחנו בשלב הראשון של האלגוריתם, בו הוא מחשב את ערכם של הקודקודים הנסתרים בהתאם לערכם של הקודקודים הגלויים, ההסתברות לכך שערכו של v תהיה 1 נתונה על ידי הנוסחא הבאה:

$P(v)={1 \over Z}\sum _{h}e^{-E(v,h)}$

הגרדיאנט הוא הנגזרת החלקית של לוגריתם פונקציית ההסתברות לפי המשקלים, ולאחר חישוב די ארוך הוא מתואר בצורה פשוטה יחסית כך:

${\partial logP(v) \over \partial w_{ij}}={<v_{i}h_{j}>_{data}-<v_{i}h_{j}>_{model}}$

הסוגריים הנטויים מסמנים תוחלת. כלל הלמידה הוא, אם כן:

$\Delta w_{ij}=\alpha ({<v_{i}h_{j}>_{data}-<v_{i}h_{j}>_{model}})$

ותוך שימוש בתכונות של RBM (הקודקודים של אותה שכבה לא מקושרים זה לזה) מתקבל חישוב פשוט יותר:

$\Delta w_{ij}=\alpha ({<v_{i}h_{j}>_{data}-<v_{i}h_{j}>_{recom}})$

ראו גם

• זכוכית ספין
• התפלגות בולצמן

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

מכונת בולצמן32650728Q194706