סדרה הנדסית אינסופית מתכנסת

סדרה הנדסית אינסופית מתכנסת היא מקרה פרטי של הסדרה ההנדסית, בו מנת הסדרה היא בין 1 לבין 1- (לא כולל הקצוות ו-0). נהוג לסמן את המנה באות q ולכן $|q|<1$.

סדרה הנדסית אינסופית שאינה מקיימת תנאי זה נקראת סדרה הנדסית מתבדרת.

הוכחת נוסחאת סכום הסדרה ההנדסית האינסופית

דיאגרמה להמחשת סכום הסדרה ההנדסית $1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}...$ המתכנסת ל-$2$

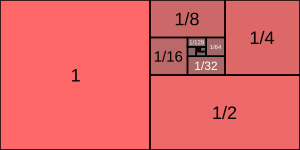
נניח כי נתונה הסדרה ההנדסית האינסופית המתכנסת $\left(a_{n}\right)_{n=1}^{\infty }=a_{1},a_{2},a_{3},a_{4},...$. על פי הגדרת הסדרה ההנדסית המתכנסת, מנת הסדרה מקיימת $|q|<1$ולכן $\lim _{n\to \infty }q^{n}=0$.

את סכום הסדרה ההנדסית המתכנסת מסמנים באות $S$ או לעיתים ב-$S_{\infty }$. ניתן לחשב את הסכום החלקי של סדרה הנדסית עם הנוסחה: $S_{n}={\frac {a_{1}(q^{n}-1)}{q-1}}$. משמעות העובדה שסכום הסדרה מתכנס היא שהגבול של הביטוי לסכום קיים. בניסוח אחר:

$$\lim _{n\to \infty }S_{n}=\lim _{n\to \infty }{\frac {a_{1}(q^{n}-1)}{q-1}}={\frac {a_{1}(\lim _{n\to \infty }q^{n}-1)}{q-1}}={\frac {a_{1}(0-1)}{q-1}}={\frac {a_{1}(-1)}{q-1}}={\frac {a_{1}}{1-q}}$$

ניתן לראות זאת גם בדוגמה מספרית. סכום הסדרה המקיימת $a_{1}=1,q={\frac {1}{2}}$ מתכנס ל-2 לפי החישוב הבא: $S={\frac {1}{1-{\frac {1}{2}}}}={\frac {1}{\frac {1}{2}}}=2$.

ראו גם

• סדרה הנדסית
• טור הנדסי

קישורים חיצוניים

• גדי אלכסנדרוביץ', מהו גבול? (של סדרה), באתר "לא מדויק", 3 באוקטובר 2010

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

סדרה הנדסית אינסופית מתכנסת25376907