תהליך סטציונרי

תהליך סטציונרי למעלה, ותהליך לא סטציונרי למטה

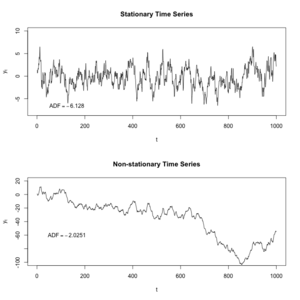
במתמטיקה וסטטיסטיקה, תהליך סטציונרי (או תהליך סטציונרי במובן הצר) הוא תהליך סטוכסטי אשר צפיפות הפילוג המשותפת אינה משתנה בהזזה בזמן. כתוצאה מכך, פרמטרים כגון תוחלת ושונות, אם הם קיימים, גם לא משתנים בזמן.

סטציונריות משמשת ככלי לניתוח סדרה עתית, שבה הדגימות לעיתים הופכות סטציונריות; לדוגמה, מידע כלכלי הוא לרוב עונתי ו/או תלוי ברמת מחירים אי-סטציונרית. סוג חשוב של חוסר סטציונריות (או אי-סטציונריות) שלא כולל צורה מגמתית מובהקת הוא התהליך הציקלוסטציונרי.

הגדרה

פורמלית, יהי $\left\{X_{t}\right\}$ תהליך סטוכסטי ויהי $F_{X}(x_{t_{1}+\tau },\ldots ,x_{t_{k}+\tau })$ פונקציית הצטברות של הפילוג המשותף של $\left\{X_{t}\right\}$ בזמנים $t_{1}+\tau ,\ldots ,t_{k}+\tau$. אזי, נאמר ש $\left\{X_{t}\right\}$  הוא תהליך סטציונרי במובן הצר אם ורק אם, עבור כל $k$, כל $\tau$ וכל $t_{1},\ldots ,t_{k}$,

$F_{X}(x_{t_{1}+\tau },\ldots ,x_{t_{k}+\tau })=F_{X}(x_{t_{1}},\ldots ,x_{t_{k}}).$

כלומר הזזה ב-$\tau$ לא משפיעה על  $F_{X}(\cdot )$  הפילוג המשותף.

צורות חלשות יותר של סטציונריות

סטציונריות במובן הרחב

צורה חלשה יותר של סטציונריות שנמצאת בשימוש בעיבוד אותות ידועה כסטציונריות במובן הרחב (wise-sense stationary או WSS). סטציונריות במובן הרחב דורשת שרק המומנט הראשון והאוטוקוואריאנס לא יהיו תלויים בזמן. כל תהליך סטציונרי במובן הצר הוא גם סטציונרי במובן הרחב.

אז, תהליך סטוכסטי בזמן רציף (x(t סטציונרי במובן הרחב מקיים את התכונה הבאה עבור התוחלת שלו:

$\mathbb {E} [x(t)]=m_{x}(t)=m_{x}(t+\tau )\,\,{\text{ for all }}\,\tau \in \mathbb {R}$

ועבור פונקציות האוטקוואריאנס שלו:

$\mathbb {E} [(x(t_{1})-m_{x}(t_{1}))(x(t_{2})-m_{x}(t_{2}))]=C_{x}(t_{1},t_{2})=C_{x}(t_{1}+(-t_{2}),t_{2}+(-t_{2}))=C_{x}(t_{1}-t_{2},0).$

התכונה הראשונה אומרת שהפונקציה (m_x(t חייבת להיות קבועה. התכונה השנייה שפונקציית האוטוקוואריאנס תלויה רק בהבדל בין $t_{1}$ ו $t_{2}$ , וצריך להיות פונקציה של משתנה אחד ולא שניים. לכן, במקום לכתוב,

$\,\!C_{x}(t_{1}-t_{2},0)\,$

הכתיב המקוצר הוא

$C_{x}(\tau )\,\!{\mbox{ where }}\tau =t_{1}-t_{2}.$

זה גם אומר שהאוטוקורלציה תלויה רק ב $\tau =t_{1}-t_{2}$, כלומר:

$\,\!R_{x}(t_{1},t_{2})=R_{x}(t_{1}-t_{2})=R_{x}(\tau )$