ויסקואלסטיות

במדעי החומר, ובראולוגיה בפרט, ויסקואלסטיות (מאנגלית: viscoelasticity; אלסטיות צמיגית) היא תכונה המתארת תגובת חומרים למאמץ. בראשית דרכו של מדע החומרים נעשתה הבחנה ברורה בין תגובת מוצקים ותגובת זורמים למאמץ. תחת מאמץ גזירה קטן, מוצק מתעוות אך חוזר לצורתו המקורית לאחר הסרת הכוח, בעוד שנוזל זורם ברציפות. בפועל, חומרים מציגים מגוון רחב של תגובות למאמץ, תגובות היכולות להיות בעל אופי אלסטי ואופי של זרימה צמיגית גם יחד.

כמו כן, ישנם חומרים המגיבים למאמץ באופן המשתנה בצורה ניכרת בהתאם לאופן הפעלת הכוח. חומר יכול להתנהג כמוצק עבור כוחות המופעלים מהר, אך כמו נוזל עבור כוחות המופעלים לאט, דוגמה מוכרת לחומר כזה היא מיסטוק (אובלק). ולהפך, ישנם חומרים שיתנהגו כמו זורם עבור כוחות מהירים, אך כמו מוצק עבור כוחות איטיים. תגובת החומר לרוב תלויה בטמפרטורה, בקצב הפעלת הכוח, ובהסטוריה של החומר.

חומרים פולימריים לעיתים קרובות מציגים תכונות ויסקו-אלסטיות בעקבות הקשרים שנוצרים בין המולקולות הארוכות. תחת מעוות המולקולות הסבוכות נמתחות ונוצר מאמץ פנימי, ולאחר זמן הקשרים נפרמים ונוצרת זרימה צמיגה שמרפה את המאמץ שנוצר. אחד הניסויים המפורסמים בתחום הוא ניסוי טיפת הזפת שמדגים כיצד סוג של זפת (Pitch) אשר נראית מוצקה, היא בעצם נוזל מאוד צמיג. הניסוי רץ ברציפות מאז 1927 ומדגים כיצד הזפת מטפטפת ממשפך בקצב של בערך טיפה אחת בעשור.

תכונות

באופן כללי, תחת מאמץ יתרחשו בחומר שינויים במבנה המיקרוסקופי של החומר. במציאות שינויים אלו קורים על פני סקלת זמן תלוית חומר. כאשר השינויים הללו קורים מאוד מהר ביחס למשך הזמן של הניסוי/תצפית, החומר יתנהג כזורם צמיג, וכל האנרגיה שתושקע בעיוות החומר תאבד לחום על ידי כוחות חיכוך פנימיים. לעומת זאת אם סקלת הזמן ארוכה מאוד ביחס למשך הניסוי, החומר יתנהג כמוצק אלסטי וכל האנרגיה שהושקעה בעיוות החומר נשמרת כאנרגיה אלסטית בחומר.

שתי ההתנהגויות הללו הן מקרי גבול אידאלים, ורוב החומרים בפועל יציגו התנהגות ויסקואלסטית. חלק מהאנרגיה תשמר כאנרגיה אלסטית, וחלק מהאנרגיה תאבד לחום על ידי כוחות חיכוך פנימיים בחומר. זה נובע מכך שהזמן הדרוש למולקולות להסתדר אינו אפסי ואינו אינסופי, ותמיד חלק מהאנרגיה תאבד לכוחות חיכוך פנימיים, אך לא כולה. בראי העובדה הזאת הוגדר מספר דבורה^[1], המאפיין היכן החומר נמצא בין זורם צמיג למוצק אלסטי לחלוטין, ומוגדר כך:

$D e = \frac{τ}{t_{e x p}}$

כאשר $τ$ הוא סקלת הזמן האופיינית לחומר^[2], ו- $t_{e x p}$ הוא משך זמן הניסוי/תצפית. כאשר $D e < < 1$ , החומר יתנהג יותר כזורם צמיג. כאשר $D e > > 1$ החומר יתנהג כמוצק.

מתיאור זה ניתן להבין מספר התנהגויות של חומרים ויסקואלסטיים הנצפות בניסויים. מזה נובע כי המאמצים הפנימיים בחומר לא תלויים רק במצב הנוכחי של החומר, אלא גם בהסטוריה של המעוות ששינתה את המבנה המיקרוסקופי של החומר. עובדה זו באה לידי ביטוי בכמה דרכים אופייניות:^[3]

היסטרזיס - על פני עיוות של החומר, והרפייתו בחזרה למצבו המקורי, ניתן לצפות בלולאת היסטרזיס בגרף מאמץ-מעוות. המאמצים הפנימיים בדרך הלוך ובדרך חזור שונים עקב שינויים במבנה המולקולרי של החומר.האנרגיה ליחידת נפח שנאבדת לחום שווה לשטח הכלוא בלולאה $E_{l o s t} = \oint σ d ϵ$ .
הרפיית מאמץ - כאשר נעוות את החומר ונחזיק אותו במעוות קבוע, עם הזמן המאמצים הפנימיים ידעכו עקב סידור מחדש של המבנה המיקרוסקופי.
זחילה - עבור מאמץ קבוע, לאחר המעוות האלסטי ה"מיידי", החומר ימשיך להתעוות בקצב איטי בעקבות שינויים בסידור המיקרוסקופי של החומר.

התכונות של חומרים ויסקואלסטיים לרוב תלויות בצורה חזקה בטמפרטורה. למשל חומרים פולימריים שמציגים התנהגות ויסקואלסטית יעברו בין כמה התנהגויות שונות בתכלית בטמפרטורות שונות. בטמפרטורות נמוכות, אין למולקולות די אנרגיה תרמית כדי לשנות קונפיגורציות, והחומר יהיה בפאזה זכוכיתית בעל מודולו אלסטיות קשיח יחסית. כאשר הטמפרטורה עולה מעל לטמפרטורה מסוימת, המולקולות יוצאות מהקיפאון ויכולות לנוע מה שגורר צניחה משמעותית של מודולו האלסטיות. בטמפרטורות גבוהות יותר החומר עובר למצב דמוי גומי. ניתן למתוח את החומר, והמולקולות הארוכות משמשות כקפיצים אנטרופיים אלסטיים. בטמפרטורות גבוהות המולקולות יכולות לנוע בחופשיות ונעות כנוזל צמיג.

ויסקואלסטיות לינארית

למען הפשטות, נדון במודל שהוא אפקטיבית חד-ממדי. נפעיל על חומר שצורתו תיבה מלבנית מאמץ גזירה (ראו איור). כאשר מפעילים על מוצק מאמץ גזירה, לפי המודל הקלסי של אלסטיות לינארית, מתקיים הקשר

$σ_{x y} = G \frac{\partial u_{x}}{\partial y} = 2 G ϵ_{x y}$

כאשר $σ, u, G, ϵ$ הם טנזור המעוות, מודולו הגזירה, וקטור ההעתק, וטנזור המאמץ בהתאמה. ובשוויון השני השתמשנו בהגדרת טנזור המעוות $ϵ_{i j} = \frac{1}{2} (\frac{\partial u_{i}}{\partial j} + \frac{\partial u_{j}}{\partial i})$ . מעתה נשמיט את האינדקסים ונסמן $σ, ϵ$ .

במודל הפשוט הזה התגובה למאמץ היא מיידית. על מנת שהתגובה תהיה תלויית זמן, ותושפע גם מההסטוריה של הפעלת המאמץ, עלינו להכליל את הנוסחה לעיל כך שתהיה תלויה בזמן^[4].

$σ (t) = \int_{- \infty}^{t} d t^{'} G (t - t^{'}) \dot{ϵ} (t^{'})$

כאשר $G$ היא כעת פונקציה התלויה בזמן, הנקראת פונקציית הרלקסציה, ו- $\dot{ϵ}$ זו הנגזרת הזמנית של $ϵ$ . זו צורה כללית להשיג תלות לינארית בין המאמץ למעוות. שימוש בויסקואלסטיות לינארית טוב בעיקר למאמצים קטנים, ועבור חומרים שלא משנים את תכונותיהם תחת מעוות. החקר של התנהגות לא לינארית מורכב בהרבה ועדיין נמצא בחזית המחקר.

כמובן שהנוסחה לעיל מכילה בתוכה גם את המקרים הפשוטים של זורם ניוטוני וחומר אלסטי לחלוטין:

עבור $G (t) = η_{0} δ (t)$ נקבל $σ (t) = η_{0} \dot{ϵ}$ . נשים לב ש $\dot{ϵ} = \frac{\partial {\dot{u}}_{x}}{\partial y} = \frac{\partial v_{x}}{\partial y}$ , כאשר $v_{x}$ זו מהירות הזרימה (קצב המעוות). קיבלנו את הקשר המוכר בין מאמץ לגרדיאנט המהירות בזורם ניוטוני.
עבור $G (t) = G_{0}$ קבוע, נקבל $σ (t) = G_{0} ϵ (t)$ בדומה לחומר אלסטי לחלוטין.

ניתן גם להפוך קשר זה ולקבל

$ϵ = \int_{- \infty}^{t} K (t - t^{'}) \dot{σ} (t^{'}) d t^{'}$

כאשר $K$ נקראת פונקציית הזחילה, ו $\dot{σ}$ הנגזרת הזמנית של המאמץ.^[4]

מודלים מכאניים

על מנת למדל חומרים מורכבים, נהוג לבנות מערכת הבנויה מרכיבים מכאניים - קפיצים ובוכנות. הקפיצים מייצגים התנהגות אלסטית לחלוטין ומצייתים לחוק הוק $σ = E ϵ$ , כאשר $E$ הוא מודולו האלסטיות של הקפיץ. הבוכנות המייצגות זרימה של זורם צמיג ומקיימות $σ = η \frac{d ϵ}{d t}$ , כאשר $η$ זוהי צמיגות הזורם. את רכיבים אלו ניתן לחבר בטור או במקביל ולקבל התנהגויות שונות. בעזרת מודלים פנומנולוגיים אלו ניתן לקבל פונקציות רלקסציה המתאימות לחומרים שונים. נציג כמה מודלים פשוטים.^[5]

מודל מקסוול

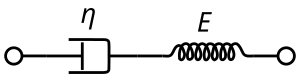
המודל מורכב מבוכנה וקפיץ המחוברים בטור. במודל זה המעוות הכולל הוא סכום המעוותים של הקפיץ והבוכנה, והמאמץ על הבוכנה והקפיץ שווים למאמץ הכולל.

$σ = σ_{η} = σ_{E} ϵ = ϵ_{E} + ϵ_{η}$

כאשר סימון תחתי $E, η$ מתייחס לבוכנה או לקפיץ בהתאמה. נגזור את נוסחת המעוותים לפי הזמן, ונציב תלות המאמץ במעוות של בוכנה ושל קפיץ ונקבל את המשוואה הדיפרנציאלית - $\dot{σ} + \frac{E}{η} σ = E \dot{ϵ}$ . נהוג להגדיר את זמן הרלקסציה $τ = \frac{η}{E}$ , הזמן האופייני שלוקח למולקולות החומר להגיב לשינוי. פתרון המשוואה הוא:

$σ = \int_{- \infty}^{t} E e^{- \frac{t - t^{'}}{τ}} \dot{ϵ}$

כלומר פונקציית הרלקסציה היא $G (t) = E e^{- \frac{t}{τ}}$ . קיבלנו שהחומר:

עבור פרקי זמן קצרים ( $t < < τ$ ) מתנהג כמוצק. האקספוננט שווה בערך ל-1, ונקבל $G (t) = E$ כמו בחומר אלסטי לחלוטין.
עבור פרקי זמן ארוכים ( $t > > τ$ ) מתנהג כמו זורם. האקספוננט שואף לאפס בדומה לפונקציית הדלתא לעיל.
עבור מעוות שהוא פונקציית מדרגה, כלומר מעוותים את החומר ב- $t = 0$ ומחזיקים אותו במצב המעוות נקבל $σ = E e^{- \frac{t}{τ}}$ . תחילה יש מאמצים פנימיים, אך הם דועכים על פני סקלת זמן $τ$ .

מודל קלווין-וויגט (Kelvin-Voigt)

המודל מורכב מקפיץ ובוכנה המחוברים במקביל. במודל זה המעוות של כל רכיב שווה למעוות הכולל, אך המאמץ הכולל הוא סכום המאמצים של שני הרכיבים. $ϵ = ϵ_{E} = ϵ_{η} σ = σ_{E} + σ_{η}$

במקרה הזה פונקציית הרלקסציה מתקבלת בצורה טריוויאלית ממשוואת המאמצים והיא שווה לסכום של שתי פונקציות הרלקסציה של הרכיבים. המודל מתאר מוצק אלסטי על פני פרקי זמן ארוכים, אך עם תוספת של התנגדות למעוות בפרקי זמן קצרים. עבור מאמץ קבוע $σ_{0}$ החל מזמן $t = 0$ , החומר ישאף אקספוננציאלית להגיע למעוות של מוצק אלסטי (ללא הבוכנה הצמיגית) $ϵ = σ_{0} / E$ על פני סקלת זמן אופיינית $τ = η / E$ , בהתאם לנוסחה:

$ϵ = \frac{σ_{0}}{E} (1 - e^{- \frac{t}{τ}})$

זהו בעצם מודל מעט יותר מציאותי למוצק ללא תגובה מיידית. לאחר הסרת המאמץ, החומר יחזור למצב שיווי המשקל שלו על פני אותה סקלת זמן (ראו איור).

מודל מוצק סטנדרטי (מודל זנר)

על מנת לתאר מוצקים בצורה מציאותית יותר, ניתן לחבר מודל בעל שלושה רכיבים.^[6] ישנן שתי דרכים לעשות זאת על מנת לקבל התנהגות דמויית מוצק (מעוות סופי בזמנים ארוכים). הטבלה מציגה את שתי הדרכים האפשריות, ואת המשוואה הדיפרנציאלית אשר מתקבלת עבור המאמץ/המעוות. זהו המודל הפשוט ביותר אשר מאפשר גם הרפייה של מאמצים פנימיים עבור מעוות קבוע, וגם זחילה עבור מאמץ קבוע.

הצגת מקסוול	הצגת קלווין-וויגט

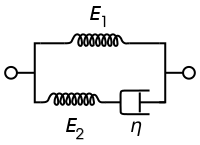
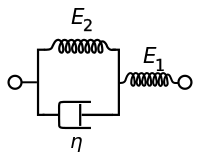
$σ + \frac{η}{E_{2}} \dot{σ} = E_{1} ε + \frac{η (E_{1} + E_{2})}{E_{2}} \dot{ε}$	$σ + \frac{η}{E_{1} + E_{2}} \dot{σ} = \frac{E_{1} E_{2}}{E_{1} + E_{2}} ε + \frac{E_{1} η}{E_{1} + E_{2}} \dot{ε}$

אמנם המודל מציג התנהגות שהיא איכותית פיזיקלית, אך בניסויים פעמים רבות יש אי התאמה בין הנתונים למודל.

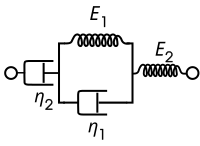
מודל ברגרס

מודל זה מוסיף למודל המוצק הסטנדרטי בוכנה נוספת על מנת לקבל התנהגות של זורם עבור הפעלת מאמץ לפרקי זמן ארוכים. גם כאן קיימות שתי הצגות של המודל והן מוצגות בטבלה יחד עם המשוואה הדיפרנציאלית המתקבלת עבור המאמץ/מעוות.

הצגת מקסוול	הצגת קלווין-וויגט

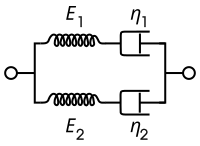
$σ + (\frac{η_{1}}{E_{1}} + \frac{η_{2}}{E_{2}}) \dot{σ} + \frac{η_{1} η_{2}}{E_{1} E_{2}} \ddot{σ} = (η_{1} + η_{2}) \dot{ε} + \frac{η_{1} η_{2} (E_{1} + E_{2})}{E_{1} E_{2}} \ddot{ε}$	$σ + (\frac{η_{1}}{E_{1}} + \frac{η_{2}}{E_{1}} + \frac{η_{2}}{E_{2}}) \dot{σ} + \frac{η_{1} η_{2}}{E_{1} E_{2}} \ddot{σ} = η_{2} \dot{ε} + \frac{η_{1} η_{2}}{E_{1}} \ddot{ε}$

מודלים לא לינאריים

חומרים רבים לא מגיבים בצורה לינארית למאמץ. מאפייני החומר אינם קבועים אלא תלויים במעוות הנוכחי של החומר. על מנת למדל חומרים אלו ניתן להוסיף רכיבים לא לינאריים למודלים שהוצגו לעיל. ניתן להחליף את הקפיצים בקפיצים לא לינאריים עם חוק הוק מוכלל - $σ = E ϵ^{n}$ . כמו כן את הבוכנות ניתן להחליף בבוכנות עם צמיגות תלויית מעוות, לדוגמה $σ = η ϵ^{n} \dot{ϵ}$ או $σ = η e^{- ϵ / ϵ_{0}} \dot{ϵ}$ . כך ניתן לשפר את ההתאמה לנתונים, אך המשוואות הדיפרנציאליות המתקבלות אינן לינאריות וקשות בהרבה לפתרון.

לקריאה נוספת

קישורים חיצוניים

מדיה וקבצים בנושא ויסקואלסטיות בוויקישיתוף

איך להכין חומר שהוא גם נוזל וגם מוצק באותו זמן, ד"ר אבי סאייג, מכון דוידסון לחינוך מדעי, אוקטובר 2011
תאוריית האלסטיות - לנדאו & ליפשיץ - אנגלית

הערות שוליים

↑ M. Reiner, The Deborah Number, Physics Today 17, 1964-01-01, עמ' 62–62 doi: 10.1063/1.3051374
↑ $τ$ יכול להיות תלוי לא רק בסוג החומר, אלא גם בקונפיגורציה הנוכחית שלו, ובטמפרטורה. בפועל לחומרים יש ספקטרום של זמני רלקסציה.
↑ Marc André Meyers, Krishan Kumar Chawla, Mechanical Behavior of Materials, Cambridge University Press, 2008-11-06, מסת"ב 978-0-521-86675-0
^ ^4.0 ^4.1 W. G. Knauss, Viscoelasticity and the Time-dependent Fracture of Polymers, Oxford: Elsevier, 2003-01-01, עמ' 854–898, מסת"ב 978-0-323-91945-6
↑ Kelly, PA, Solid Mechanics On-line Books, pkel015.connect.amazon.auckland.ac.nz
↑ Nicholas W. Tschoegl, The Phenomenological Theory of Linear Viscoelastic Behavior, 1989 doi: 10.1007/978-3-642-73602-5

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

ויסקואלסטיות41802319Q910483

[1] M. Reiner, The Deborah Number, Physics Today 17, 1964-01-01, עמ' 62–62 doi: 10.1063/1.3051374

[2] $τ$ יכול להיות תלוי לא רק בסוג החומר, אלא גם בקונפיגורציה הנוכחית שלו, ובטמפרטורה. בפועל לחומרים יש ספקטרום של זמני רלקסציה.

[3] Marc André Meyers, Krishan Kumar Chawla, Mechanical Behavior of Materials, Cambridge University Press, 2008-11-06, מסת"ב 978-0-521-86675-0

[:02-4] 4.0 ^4.1 W. G. Knauss, Viscoelasticity and the Time-dependent Fracture of Polymers, Oxford: Elsevier, 2003-01-01, עמ' 854–898, מסת"ב 978-0-323-91945-6

[5] Kelly, PA, Solid Mechanics On-line Books, pkel015.connect.amazon.auckland.ac.nz

[6] Nicholas W. Tschoegl, The Phenomenological Theory of Linear Viscoelastic Behavior, 1989 doi: 10.1007/978-3-642-73602-5

[1]

[2]

[3]

[4]

[5]

[6]

ויסקואלסטיות

תוכן עניינים

תכונות