משפט הקליפה

במכניקה קלאסית, משפט הקליפה (באנגלית: Shell theorem) מפשט בעיות גרביטציוניות הקשורות בכוח המשיכה שפועל על גופים מבחוץ או מבפנים לגוף בעל סימטריה כדורית. למשפט זה יש חשיבות רבה באסטרונומיה.

אייזק ניוטון הוכיח את משפט הקליפה וקבע ש-:

1. גוף בעל סימטריה ספירית משפיע כבידתית על גופים אחרים באותו אופן כאילו כל המסה שלו הייתה מרוכזת בנקודה אחת שהיא מרכזו.

2. אם גוף הוא קליפה כדורית אחידה (כדור חלול), היא לא מפעילה כוח כבידתי על עצם שנמצא בתוכה, וללא קשר למיקומו של העצם בחלק הפנימי שלה.

כמסקנה מן המשפט נובע שבתוך כדור עם צפיפות מסה אחידה, הכוח הכבידתי משתנה ליניארית עם המרחק מהמרכז, ונהיה אפס במרכז הכדור.

התוצאות האלה היו חשובות לאנליזה של ניוטון את התנועות הפלנטריות; הן לא ברורות מאליו - ההוכחה המקורית של ניוטון עשתה שימוש ארוך בחשבון אינפיניטסימלי, בניגוד להוכחה המודרנית הפשוטה למשפט הקליפה הנעזרת בחוק גאוס לכבידה.

בנוסף לכבידה, משפט הקליפה יכול להיות מיושם גם כדי לתאר את השדה החשמלי הנוצר על ידי קליפה כדורית הטעונה בצפיפות מטען חשמלי אחידה, או באופן דומה לכל תופעה אחרת שנשלטת על ידי חוק היפוך ריבוע.

משיכה כבידתית מבחוץ לקליפה

גוף מוצק בעל סימטריה כדורית ניתן למידול כמספר אינסופי של קליפות כדוריות קונצנטריות בעובי אינפיניטסימלי. אם נוכיח שקליפה כדורית יוצרת שדה כבידה זהה לזה של מסה נקודתית הממוקמת במרכזה, אז ינבע מכך שמערכת של קליפות כאלה (כמו כדור) גם מפעילה משיכה כאילו כל המסה שלה הייתה מרוכזת במרכזה.

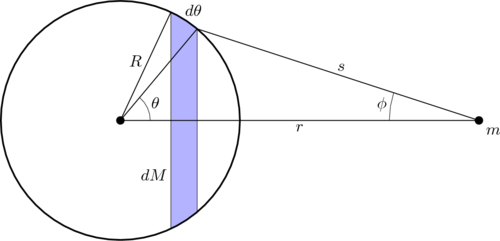
ראשית נחלק את הקליפה הכדורית לאוסף של פרוסות מעגליות ברדיוס משתנה, כך שכל הנקודות על פרוסה מעגלית נמצאות באותו מרחק $s$ מהחלקיק החיצוני (הפרוסה היא בעצם הפס המוכחל באיור). לפי חוק הכבידה העולמי של ניוטון, הכוח שמפעיל אלמנט מסה על פרוסה מסוימת על חלקיק חיצוני הוא:

$dF={\frac {Gm\;dM}{s^{2}}}$

עם זאת, כיוון שאודות לטבע הווקטורי של הכוח אלמנטים שונים של מסה על הפרוסה מבטלים חלקית את הכוחות שמפעילים אלמנטים אחרים של המסה, סה"כ הכוח שיוצרת הפרוסה בכיוון r (הרדיוס שמחבר בין החלקיק החיצוני ומרכז הקליפה) הוא:

$F_{r}={\frac {Gm\;dM_{s}}{s^{2}}}\cos \phi .$

כאשר $dM_{s}$ הוא סה"כ המסה של הפרוסה שמתאימה למרחק s מהחלקיק. הכוח הכולל על m, הוא פשוט סכום הכוחות שיוצרת כל אחת מהפרוסות המעגליות בנפרד. הסכום הזה יכול להיות מיוצג באמצעות האינטגרל הבא:

$F_{r}=\int dF_{r}$

כיוון ש-G ו-m הם קבועים, ניתן להוציא אותם מהאינטגרל ולקבל:

$F_{r}=Gm\int {\frac {dM_{s}\cos \phi }{s^{2}}}.$

כדי להעריך את האינטגרל הזה, נכתוב את $dM_{s}$ כפונקציה של הזווית θ והדיפרנציאל שלה dθ. השטח הכולל של קליפה כדורית הוא: $4\pi R^{2}$, בעוד השטח של פרוסה דקה בין הזוויות θ ו-θ + dθ הוא:

$2\pi R^{2}\sin \theta \,d\theta$.

לכן, אם המסה של הקליפה היא M, נקבל ש-:

$dM_{s}={\frac {2\pi R^{2}\sin \theta }{4\pi R^{2}}}M\,d\theta =\textstyle {\frac {1}{2}}M\sin \theta \,d\theta$

וש-:

$F_{r}={\frac {GMm}{2}}\int {\frac {\sin \theta \cos \phi }{s^{2}}}\,d\theta$

לפי משפט הקוסינוסים:

$\cos \phi ={\frac {r^{2}+s^{2}-R^{2}}{2rs}}$

$\cos \theta ={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.$

שתי המשוואות האלה קושרות בין שלושת הפרמטרים θ, s ו-φ שמופיעים באינטגרל יחדיו. כאשר θ עולה מ-0 ל- π רדיאנים, φ עולה מערך התחלתי אפס לערך מקסימלי ולאחר מכן מתחיל לרדת בחזרה עד ל-0 (כאשר θ = π). הפרמטר s לעומת זאת גדל מערך התחלתי של r − R לערך סופי של r + R כאשר θ גדל מ-0 ל- π רדיאנים. הסיטואציה כולה מומחשת באנימציה הבאה.

כדי להפוך את האינטגרנד לפונקציה של משתנה אחד, צריך להפוך s למשתנה אינטגרציה בלתי תלוי. באמצעות גזירה של הביטוי השני של חוק הקוסינוסים ניתן לקבל:

$\sin \theta \;d\theta ={\frac {s}{rR}}ds.$

ומכך מקבלים ש-:

$F_{r}={\frac {GMm}{2rR}}\int {\frac {\cos \phi }{s}}\,ds$

כאשר משתנה האינטגרציה החדש s משתנה בין הגבולות r − R ל- r + R. לסיום, נחליף כעת את (cos(φ בביטוי של s באמצעות המשוואה הראשונה של חוק הקוסינוסים ונקבל:

$F_{r}={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\,ds.$

הפונקציה הקדומה לאינטגרנד היא:

$s-{\frac {r^{2}-R^{2}}{s}}$

אם נציב את הגבולות r − R ו-r + R במשתנה האינטגרציה בפונקציה הקדומה הזאת, מקבלים את התוצאה:

$F_{r}={\frac {GMm}{r^{2}}},$.

משיכה כבידתית בתוך הקליפה

בעבור נקודה בתוך הקליפה, ההבדל הוא שכאשר θ שווה לאפס, φ מקבל את הערך π רדיאנים ו-s את הערך R - r. כאשר θ עולה מ-0 ל-π רדיאנים, φ קטן מהערך ההתחלתי של π רדיאנים ל-0 ו-s משתנה מ-R - r ל-R + r.

ניתן לראות את התמונה באיור הבא.

אם נציב את הגבולות האלה בפונקציה הקדומה:

$s-{\frac {r^{2}-R^{2}}{s}}$

נקבל במקרה זה ש-:

$F_{r}=0$.

הכללות

אחת התוצאות המרכזיות בפרינקיפיה של ניוטון היא ההוכחה שגופים מסתחררים יאמצו צורה ספרואידית כתוצאה משילוב ההשפעות של הכבידה העצמית והסיבוב העצמי שלהם. כיוון שרבים מהגופים במערכת השמש מגלים סיבוב עצמי, קירוב הצורה הכדורית לא תקף להם, ונוצר הצורך בכלים אנליטיים חזקים יותר כדי לתאר את הכבידה שמפעיל האליפסואיד הכללי. בעיה חשובה זו העסיקה מתמטיקאים ואסטרונומים רבים מאז פרסום חוק הכבידה העולמי על ידי ניוטון ב-1687, בהם קולין מקלורן, פייר-סימון לפלס, ז'וזף לואי לגראנז' ועוד. הראשון שהצליח לגזור ביטוי מתמטי מפורש לכבידה בחלק הפנימי של אליפסואיד הומוגני היה קרל פרידריך גאוס במאמר משנת 1813 שדן בכוח הכבידה שיוצר אליפסואיד הומוגני. גאוס גזר את הביטוי הבא לכוח המשיכה בתוך האליפסואיד: $g_{i}=2\pi G\rho A_{i}x_{i}$, כאשר:

$A_{i}=a_{1}a_{2}a_{3}\int _{0}^{\infty }{\frac {du}{(a_{i}^{2}+u)\Delta }}$

ו-$\Delta ^{2}=(a_{1}^{2}+u)(a_{2}^{2}+u)(a_{3}^{2}+u)$. כאן $g_{i}$ הוא רכיב שדה הכבידה המקביל לציר ה-i של האליפסואיד, $x_{i}$ הוא המרחק ממרכז האליפסואיד בכיוון המקביל לציר ה-i שלו, ו-$\rho$ היא צפיפות המסה של האליפסואיד.

למשל, במקרה של כדור נקבל, ששלושת חצאי הצירים של האליפסואיד $a_{1},a_{2},a_{3}$ שווים באורכם ושווים ל-$R$ (רדיוס הכדור), והאינטגרל שווה כעת ל-${\frac {2}{3R^{3}}}$, כך שהביטוי למשיכה הכבידתית בתוך הכדור הוא: $g_{i}={\frac {4}{3}}\pi G\rho x_{i}$, וזוהי בדיוק התוצאה שתתקבל על ידי חישוב בדרך הרגילה.

קישורים חיצוניים

מדיה וקבצים בנושא משפט הקליפה בוויקישיתוף

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

33594696משפט הקליפה