משפט תבנין
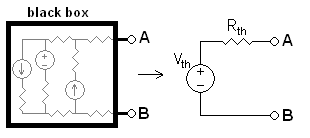
משפט תבנין (Thévenin) למעגלים חשמליים לינאריים קובע שכל צירוף של מקורות מתח, מקורות זרם ונגדים בעלי שני הדקים שקול חשמלית למקור מתח יחיד ונגד יחיד המחובר אליו בטור. עבור מעגלי AC הפועלים בתדירות יחידה המשפט ניתן ליישום גם לגבי אימפדנסים כלליים, ולא רק לנגדים. המשפט קובע שניתן להפוך מעגל הבנוי ממקורות מתח ונגדים לשקול תבנין, שהוא שיטת פישוט המשמשת לניתוח מעגלים. ניתן להשתמש בשקול תבנין כמודל לאספקת כוח או לסוללה (כאשר הנגד מייצג את ההתנגדות הפנימית והמקור מייצג את הכוח אלקטרו מניע). המעגל מכיל מקור מתח אידאלי בטור לנגד אידאלי.
המשפט התגלה לראשונה על ידי המדען הגרמני הרמן פון הלמהולץ בשנת 1853, ונתגלה שוב בשנת 1883 על ידי מהנדס הטלגרף הצרפתי לאון שארל תבנין (1857–1926).
חישוב שקול תבנין
במציאת שקול תבנין יש להבחין במעגל המקורי בין חלק המעגל שאותו רוצים להחליף בשקול, לבין חלק המעגל המוגדר כעומס, ואותו אין מחליפים. העומס אינו משפיע על השקול המתקבל, וההשפעה היחידה שלו היא בצורת החיבור של שני הדקיו לחלק המעגל שאותו מחליפים. לעיתים (כמו בציור שלעיל), העומס אינו מופיע במפורש, אבל הדקיו חייבים להיות מוגדרים בצורה ברורה.
כדי לחשב את המעגל השקול, יש לדעת את ההתנגדות ואת המתח - שני נעלמים, ולכן דרושות שתי משוואות. מקבלים שתי משוואות אלו בדרך כלל על ידי ביצוע השלבים הבאים, אם כי כל זוג תנאים שמציבים על הדקי המעגל יעבדו:
- חישוב מתח ההדקים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{AB} \!\ } בתנאי נתק, כלומר כאשר לא מחובר נגד עומס בין ההדקים - התנגדות אינסופית. זהו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{th} \!\ } .
- חישוב זרם ההדקים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{AB} \!\ } בתנאי קצר, כלומר כאשר ההדקים מקוצרים - התנגדות אפס. זהו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{th} \!\ } .
מחשבים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{th} \!\ } לפי:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{th} = \frac{V_{th}}{I_{th}} \!\ }
המעגל השקול הוא מקור מתח שמתחו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{th} \!\ } בטור לנגד שהתנגדותו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{th} \!\ } .
את תנאי 2 ניתן גם לחשב באופן הבא:
- 2א. החלפת מקורות מתח אידאליים בקצר ומקורות זרם אידאליים בנתק. מקורות בעלי התנגדות פנימית מוחלפים בהתנגדות הפנימית שלהם.
- 2ב. חישוב ההתנגדות הכוללת של המעגל בין שני ההדקים. זהו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{th} \!\ } .
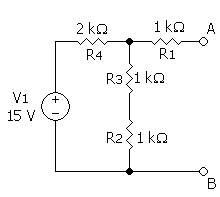
דוגמה
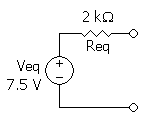חישוב המתח השקול שבדוגמה:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\mathrm{AB} = {R_2 + R_3 \over (R_2 + R_3) + R_4} \cdot V_\mathrm{1} = {1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \over (1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega) + 2\,\mathrm{k}\Omega} \cdot 15 \mathrm{V} = 7.5 \mathrm{V}}
(הנגד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1 \!\ } אינו נלקח בחשבון מאחר שהחישוב נעשה בתנאי נתק בין A ל-B, כך שלא זורם זרם דרך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_1 \!\ } ולכן גם לא נופל עליו מתח)
חישוב ההתנגדות השקולה:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_\mathrm{AB} = R_1 + \left ( \left ( R_2 + R_3 \right ) \| R_4 \right ) = 1\,\mathrm{k}\Omega + \left ( \left ( 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega \right ) \| 2\,\mathrm{k}\Omega \right ) }
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 1\,\mathrm{k}\Omega + \left({1 \over ( 1\,\mathrm{k}\Omega + 1\,\mathrm{k}\Omega )} + {1 \over (2\,\mathrm{k}\Omega ) }\right)^{-1} = 2\,\mathrm{k}\Omega }
המרה משקול נורטון
שקול נורטון כולל מקור זרם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{no} \!} ונגד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{no} \!} המחובר אליו במקביל.
שקול נורטון קשור לשקול תבנין על ידי המשוואות הבאות:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{th} = R_{no} \!}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{th} = I_{no} R_{no} \!}
מגבלות ביישום
- מעגלים רבים הינם לינאריים רק עבור תחום מסוים של עומסים, כך שמשפט תבנין לא תמיד יהיה נכון.
- שקול תבנין הוא שקול רק מנקודת המבט של העומס. צריכת ההספק בתוך שקול תבנין לא מייצגת את צריכת ההספק בתוך המערכת האמיתית.
ראו גם
קישורים חיצוניים
משפט_תבנין21815828Q241868