ספרטריקס

במתמטיקה, ספרטריקס הוא כינויו של הגבול המפריד (Separate; ומכאן שמו) בין אזורים של המישור שבהם משוואה דיפרנציאלית בשני משתנים מפגינה התנהגויות שונות. הספרטריקס מפריד בין עקומות פאזה בעלות מאפיינים שונים.

רקע

אם $\ {\frac {dx}{dt}}=f(x,y),\ {\frac {dy}{dt}}=g(x,y)$ היא משוואה דיפרנציאלית במשתנים תלויי-הזמן $\ (x(t),y(t))$ , אז התנועה שהמשוואה מגדירה בכל נקודה במישור תלויה במקדמים הראשונים של פיתוח טיילור של $f$ ושל $g$ . באופן סכימתי אפשר להבחין בין מסלולים "אליפטיים" (סגורים), "היפרבוליים" (פתוחים, המתרחקים במהירות גדלה), ו"פרבוליים" (מצב ביניים). הספרטריקס הוא העקום המישורי המפריד בין ההתנהגות האליפטית להתנהגות ההיפרבולית.

דוגמה

מטוטלת

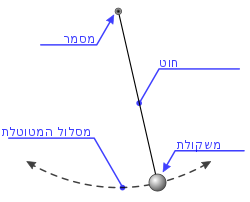
אחד מהמקרים הפשוטים בהם ניתן להבחין בקיומו של ספרטריקס הוא פתרון משוואת המטוטלת הפשוטה:

{d^{2}\theta  \over dt^{2}}+{g \over l}\sin \theta =0.

כאשר $l$ מציין את אורך המטוטלת, $g$ את תאוצת הכבידה ו- $\theta$ את הזווית בין המטוטלת לבין האנך. במערכת זו, ההמילטוניאן הוא גודל שמור וגודלו נתון על ידי

$H={\frac {{\dot {\theta }}^{2}}{2}}-{\frac {g}{l}}\cos \theta .$

משוואה זאת מתארת את התנועה של מטוטלת: כלומר של משקולת התלויה על חוט. למטוטלת כזאת ישנם שני סוגי תנועה: כאשר אין למטוטלת אנרגיה קינטית מספיק גבוהה אזי המטוטלת תבצע תנודות סביב נקודת המינימום שלה. לעומת זאת אם נדחוף את המטוטלת בכח גדול מספיק אזי היא תבצע סיבובים סביב המסמר.

מרחב הפאזה עבור מטוטלת פשוטה. הספרטריקס מודגש.

כאשר ההמילטוניאן $H$ קבוע, ניתן לשרטט את הפתרון במרחב הפאזה, כלומר לבדוק את התלות בין המהירות הזוויתית של המטוטלת ${\dot {\theta }}$ לבין הזווית $\theta$ . אופי המסלול (שהוא הפתרון של המשוואה) תלוי בגודלו של ההמילטוניאן:

אם $-{\frac {g}{l}}<H<{\frac {g}{l}}$ העקומה תהיה סגורה. אם $H$ קטן מאוד, העקומה תהיה דמוית-מעגל, וכל ש- $H$ יגדל בערכו המוחלט כך תימתח העקומה הסגורה לצורה דמוית-עין. עקומות אלו, המייצגות פתרון מסוים של המשוואה הדיפרנציאלית, משמעותן הפיזיקלית היא שהמטוטלת מתנודדת מצד לצד.
אם ${\frac {g}{l}}<|H|$ אז העקומה פתוחה, כלומר המטוטלת איננה מבצעת תנודות, ובמקום זאת היא נעה במעגלים שלמים.