עץ 2-3
במדעי המחשב, עץ 2-3 (באנגלית: 2-3 tree) הוא מבנה נתונים מסוג עץ חיפוש מאוזן. בעץ זה:
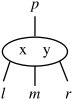
- כל צומת אב (צומת פנימי) מכיל מפתח אחד ושני בנים (צומת-2, איור 1), או שני מפתחות ושלושה בנים (צומת-3, איור 2).
- כל הצמתים ללא בנים (צמתים חיצוניים או עלים), נמצאים באותו העומק (ראה איור 3).
כמו כן, עץ ריק ועץ עם עלה אחד הם עצי 2-3.
-
איור 1 - צומת-2
-
איור 2 - צומת-3

לעץ 2-3 מספר גרסאות בעלות תכונות שונות מעט, אשר נבחרות על פי התאמתן לשימוש מסוים[1]. בגרסה המתוארת כאן, הרשומות (המכילות מפתח וערך הקשור אליו) נמצאות רק בעלים, בעוד הצמתים הפנימיים מכילים מידע לארגון בלבד. בכל צומת פנימי,
- הערך- מכיל תמיד את המפתח המקסימלי המצוי בתת-העץ השמאלי המחובר ל-.
- תת-העץ המרכזי המחובר ל- מכיל מפתחות הגדולים מ-.
- בצומת-3, הערך מכיל את המפתח המקסימלי המצוי בתת-העץ המרכזי המחובר ל-.
- בצומת-3, תת-העץ הימני המחובר ל- מכיל מפתחות הגדולים מ-.
בעץ 2-3 עם רמות, יש בין ל- עלים (כאשר העץ מורכב מצמתים מסוג צומת-2 בלבד, או צומת-3 בלבד, בהתאמה). במילים אחרות, על מנת ליצג רשומות, יש צורך בעץ עם לפחות רמות, אך לא יותר מ- רמות. משמע, כל המסלולים בעץ הם באורך .
מבנהו של עץ 2-3 מבטיח חיפוש, הכנסה, והוצאת מפתח (המיצג רשומה) בסיבוכיות במקרה הגרוע ביותר, כאשר הוא מספר המפתחות (רשומות) בעץ.
עץ 2-3 פותח על ידי ג'ון הופקרופט בשנת 1970[2][3], ושייך למשפחה של עצי חיפוש המאזנים את עצמם (Self-balancing search tree). בעצים מסוג זה פעולות הכנסת מפתח והוצאת מפתח עשויות לגרום שינויים במבנה העץ, לשם שימור איזונו. דוגמאות נוספות לעצי חיפוש המאזנים את עצמם הן: עץ AVL, עץ אדום שחור, עץ 2-3-4, ועץ B.
חיפוש

חיפוש רשומה שלה מפתח מתקדם במורד העץ כאשר בכל צומת:
- אם ממשיכים לתת-העץ השמאלי.
- אם והצומת הוא צומת-2, ממשיכים בתת-העץ הימני.
- אם והצומת הוא צומת-3, אזי אם ממשיכים בתת-העץ האמצעי, אחרת ממשיכים בתת-העץ הימני.
בסופו של דבר מגיעים לעלה. אם הרשומה נמצאת בעץ, אזי העלה יכיל את המפתח ואת הרשומה השייכת לו (ראה איור 4). אם רוצים רק לוודא את הימצאות הרשומה, ולא לגשת אליה, אפשר לעצור בכל שלב בו או .
הכנסה
אם העץ הוא ריק, מוסיפים את הרשומה בעלה, במקומו של השורש. אם העץ מכיל עלה אחד, מוסיפים צומת-2 כשורש, ואת שני העלים כבניו (ראה איור 5).
בעץ עם צמתים פנימיים, הכנסת רשומה חדשה עם מפתח מתקדמת כמו חיפוש, עד אשר מגיעים ל-, הצומת הפנימי האחרון לפני העלים.
אם צומת הוא צומת-2, מוסיפים לו עוד בן (עלה) והופכים אותו לצומת-3, כאשר העלים ממוינים והערכים מעודכנים כנדרש. אם הוא הערך הגדול מבין שלושת הבנים, יש לעדכן גם את הערכים או של האבות של הצומת (ראה איור 6).
אם צומת הוא צומת-3, מרחיבים אותו זמנית לצומת-4 (האסור בעץ 2-3), ומוסיפים לו עלה במקום המתאים. על מנת לשמור על מבנה העץ, מפצלים את צומת-4 שנוצר לשני צמתים-2, ו-. את זוג המפתחות הנמוכים מציבים בצומת השמאלי , ואת זוג המפתחות הגבוהים מציבים בצומת הימני . כעת מוסיפים את הצומת החדש שנוסף () לאב של צומת המקורי. תהליך זה זהה להוספת עלה לצומת פנימי - אם צומת הוא צומת-2 הוא יהפוך לצומת-3, ואם הוא צומת-3 הוא יעבור הרחבה לצומת-4 ופיצול. כך ממשיכים בסדרה של הרחבות ופיצולים עד אשר מגיעים לצומת-2 או מפצלים את השורש (ראה איור 7).
פיצול השורש הוא מקרה מיוחד, אשר גורם ליצירת שורש חדש מסוג צומת-2 אשר בניו הם שני הצמתים שאליהם פוצל השורש הקודם. באופן זה גדל העומק של עץ 2-3.
-
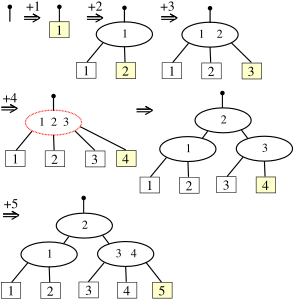
איור 5 - הכנסת המפתחות 1 עד 5, החל מעץ ריק.
-
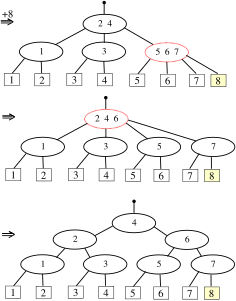
איור 6 - הכנסת המפתחות 6 עד 7.
-
איור 7 - הכנסת המפתח 8.
הוצאה
הוצאת רשומה עם מפתח מתקדמת כמו חיפוש, עד אשר מגיעים ל-, הצומת הפנימי האחרון לפני העלים.
אם צומת הוא צומת-3, מסירים את הבן עם מפתח , והופכים אותו לצומת-2. אם הבן שהוסר היה הגדול משלושת הבנים, יש לעדכן גם את הערכים או של האבות של הצומת (ראה איור 8).
אם צומת הוא צומת-2, מסירים את הבן עם מפתח , והופכים אותו זמנית לצומת-1, האסור בעץ 2-3. על מנת לשמר את מבנה העץ מבצעים את אחת מפעולות המיזוג הבאות:
- אם לצומת יש אח מימין או משמאל שלו 3 בנים, מעבירים את אחד הבנים של לצומת , ומעדכנים את הערכים או של האבות של הצומת במידת הצורך.
- אם לצומת יש רק אחים מסוג צומת-2, אזי מסירים את הבן היחיד של , מעבירים אותו לאחד מהאחים של , ומוחקים את צומת מהאב שלו .
- אם האב נותר צומת-2, התהליך הסתיים. אם האב נותר צומת-1 (האסור בעץ 2-3), חוזרים על תהליך המיזוג כפי שתואר לעיל (ראה איור 9).
אם בסוף התהליך השורש נותר צומת-1, מוחקים את השורש והופכים את בנו היחיד לשורש החדש. באופן זה קטן עומקו של עץ 2-3.
-
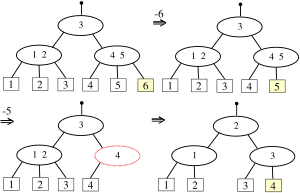
איור 8 - הסרת המפתחות 6 ו-5.
-
איור 9 - הסרת המפתחות 4, 3, 2, ו-1.
יצוג כעץ בינארי


עץ 2-3 ניתן לייצג גם באמצעות צמתים מסוג צומת-2 בלבד, כאשר מוסיפים לכל קשת עוד סיבית אשר מסמנת האם הקשת היא קשת אופקית או אנכית. כפי שניתן לראות באיור 10, ניתן לפצל כל צומת-3 לשני צמתים מסוג צומת 2, המחוברים בקשת אופקית, אותה נהוג לסמן באדום. שני הייצוגים האפשריים הם שקולים.
העץ הבינארי המתקבל מהמרת עץ 2-3 באופן זה (ראה איור 11), הוא עץ מאוזן, במובן הבא:
- העץ הוא "מאוזן שחור", כלומר כל המסלולים בין השורש לעלים עוברים דרך אותו מספר קשתות שחורות. תכונה זו מתקיימת מכיוון שהקשתות השחורות הן הקשתות המקוריות של עץ 2-3, שהוא מאוזן באופן מושלם.
- המסלול הארוך ביותר מהשורש לעלה כלשהו, ארוך לכל היותר פי שניים מהמסלול הקצר ביותר מהשורש לעלה כלשהו. מצב זה עשוי להתקבל כאשר בעץ 2-3 עם שורש מסוג צומת-3, תת-העץ הימני מורכב רק מצמתים מסוג צומת-3, בעוד תת-העץ השמאלי מורכב מצמתים מסוג צומת-2. מסלול אחד לפחות בתת-העץ הימני יהיה מורכב מקשת אדומה ושחורה לסירוגין, בעוד בתת-העץ השמאלי כל המסלולים שחורים.
מתברר[2] שפעולות האיזון המתבצעות בעץ 2-3 בעת הכנסה והוצאה של מפתח (הרחבה ופיצול, מחיקה ומיזוג), מתבטאות ביצוג כעץ בינארי המתקבל לאחר המרה, כפעולות דומות לפעולות האיזון בעץ AVL (סיבוב העץ).
מכיוון שכך, גם ביצוג כעץ בינארי של עץ 2-3 פעולות החיפוש, ההכנסה, וההוצאה של מפתח מתבצעות בסיבוכיות במקרה הגרוע ביותר.
היצוג כעץ בינארי של עץ 2-3 היווה את הבסיס לפיתוח עץ אדום שחור, שהוא עץ החיפוש הבינארי המאוזן הפופולרי ביותר במימושים מעשיים.
הרחבות וגרסאות נוספות
כאמור לעץ 2-3 מספר אפשרויות ליחוס הרשומות לצמתים, הנבחרות לפי התאמתן לשימוש מסוים[1]. לדוגמה, בגרסה אחת של עץ 2-3 הרשומות נשמרות גם בצמתים פנימיים וגם בעלים[4], ללא שכפול. באופן זה מספר הצמתים בעץ זהה למספר הרשומות, בניגוד לגרסה המתוארת לעיל, בה נשמרות הרשומות רק בעלים. למרות הבדלים אלה, פעולות האיזון בהכנסת מפתח (הרחבה ופיצול) והוצאת מפתח (מחיקה ומיזוג) זהות למעשה בכל הגרסאות.
עץ-B הוא הרחבה של עץ 2-3[5] - עץ 2-3 ידוע גם בשם "עץ-B מדרגה 3".
לקריאה נוספת
- Robert Sedgewick, Kevin Wayne, Algorithms, 4th ed., Addison-Wesley (2011). Chapter 3.3 (book-site: http://algs4.cs.princeton.edu).
קישורים חיצוניים
- עץ 2-3, מצגת מקורס מבנה נתונים, מדעי המחשב, הטכניון.
- עץ 2-3 , באתר הקורס CS367 באוניברסיטת ויסקונסין. 2005.
הערות שוליים
- ^ 1.0 1.1 Mark R. Brown and Robert E. Tarjan, Design and Analysis of a Data Structure for Representing Sorted Lists, SIAM J. Comput., 9(3), pp. 594–614, 1979.
- ^ 2.0 2.1 Knuth, Donald. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. מסת"ב 0-201-89685-0. Page 476 of section 6.2.3.
- ↑ Alfred V. Aho, J.E. Hopcroft, Jeffrey D. Ullman, The Design and Analysis of Computer Algorithms, Addison-Wesley Series in Computer Science and Information Processing (1974).
- ↑ Robert Sedgewick, Kevin Wayne, Algorithms, 4th ed., Addison-Wesley (2011). Chapter 3.3.
- ↑ Douglas Comer, The Ubiquitous B-Tree, Computing Surveys, Vol ll, No 2, June 1979. pdf
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |
עץ 2-338062657Q169338