עץ חיפוש
במדעי המחשב עץ חיפוש הוא מבנה נתונים ממוין, המאפשר הכנסה, הוצאה וחיפוש מהירים. עץ החיפוש מתבסס על מבנה העץ בתורת הגרפים.
הגדרות
עבור עץ G וצמתים v ,u
- צומת v הוא צאצא של u אם קיים מסלול מכוון מצומת u ל-v.
- u אב-קדמון של v אם v צאצא של u.
- תת-עץ של G ששורשו v הוא עץ מכוון שצמתיו הם v עצמו וכל הצאצאים של v, והקשתות שלו הן הקשתות המחברות צמתים אלו ב-G.
- דרגת צומת v היא מספר הצאצאים של v.
- עלה הוא צומת ללא צאצאים.
- צומת פנימי הוא צומת שאינו עלה.
- עומק של צומת v הוא מספר הקשתות משורש העץ אל v (המרחק מהשורש).
- גובה של צומת v הוא מספר הקשתות מ-v לצאצא הרחוק ביותר של v (עלה).
- גובה העץ הוא הגובה של שורשו.
עץ חיפוש בינארי

עץ חיפוש בינארי הוא עץ הנתונים הפופולרי ביותר. בעץ זה יש לכל קודקוד שני בנים לכל היותר, ימני ושמאלי. הבן הימני, יחד עם כל צאצאיו, נמצא ביחס הסדר אחרי הקודקוד שממנו הוא יוצא, ואילו הבן השמאלי וכל צאצאיו קודמים לקודקוד האב ביחס הסדר.
כדי להוסיף קודקוד חדש לעץ יעבור האלגוריתם על כל קודקוד וקודקוד החל מהשורש, וינוע ימינה כאשר מפתח הקודקוד הנוכחי במסלול קטן מהמפתח של הקודקוד המוכנס, ושמאלה במקרה ההפוך. האלגוריתם ייעצר ויבצע את ההוספה במקום שבו המסלול ייגמר.
כדי למחוק קודקוד יש תחילה למצוא אותו, ולאחר מכן אם הוא עלה פשוט למחוק אותו, אם יש לו בן אחד בלבד למחוק ולהפוך את הבן הזה לבן של האבא של מה שמחקנו, ואם יש לו שני בנים, למצוא את העוקב (הקודקוד הקטן ביותר שגדול ממנו) שבהכרח אין לו בן שמאלי, למחוק את העוקב ולהחליף את הקודקוד שלנו בעוקב. לשם ביצוע פעולות אלו ביעילות יש לשמור גם מצביע להורה.
מאחר שלעץ בינארי יש שני בנים, הרי שבמקרה של עץ מלא במידה שווה, גובהו יהיה Log n, עבור n נתונים (log בסיס 2). במצב כזה חיפוש בעץ יימשך פרק זמן קצר יחסית הנמצא בסיבוכיות לוגריתמית למספר הנתונים. אומנם, ייתכנו מקרים גרועים, למשל הכנסה בסדר ממוין מראש, שבהם גובה העץ יהיה n, ועלות החיפוש גבוהה. סיבוכיות הזמן בחיפוש נתון בעץ חיפוש בינארי היא (O(n במקרה הגרוע ו-((O(log(n במקרה הממוצע.
כדי להבטיח שמצב כזה לא יתרחש פותחו אלגוריתמים משוכללים להכנסה לעצים בינאריים ולמחיקה מהם באופן המבטיח שגובה העץ לא יהיה גדול מדי. עליהם מבוססים כמה עצי נתונים בינאריים חשובים.
עצים בינאריים נפוצים
- עצי AVL
- מבנה שהחיפוש בו, ההכנסה והמחיקה בו חסומים בסיבוכיות log n. בעץ זה, במקרה שיש פער של שתי רמות גובה בין צאצאיו של קודקוד מסוים מתבצע סיבוב או סיבוב כפול המחזירים את האיזון למקומו. החזרת האיזון אחרי מחיקה היא יותר סבוכה, אך גם היא חסומה בסיבוכיות לוגריתמית.
- עצים אדומים־שחורים
- עצים שבהם כל קודקוד צבוע באדום או בשחור, אך עם שתי הגבלות עיקריות: כל מסלול שייצא מהשורש יעבור עד סיומו על מספר זהה של קודקודים שחורים, וכן שלקודקוד אדום לא יהיו בנים אדומים. הגבלות אלו מבטיחות שאורך המסלול המקסימלי לא יעלה על כפליים אורכו של המסלול המינימלי, ובכך מחייבות סיבוכיות לוגריתמית. האלגוריתם של עצי אדום שחור הוא סבוך יותר מזה של עצי AVL, אך נחשב למעט מהיר יותר. כל עץ AVL יכול להיחשב תקין על פי כללי עץ אדום שחור, אך לא ההפך.
- עצי Splay
- עצים המבוססים על העלאה לשורש של כל קודקוד שנעשה עליו חיפוש. עצים אלו ייתנו תוצאה טובה כאשר קיימים הבדלי תדירויות בגישה לפריטים. מסלול הבאתו של הקודקוד המבוקש אל השורש מלווה בסיבובים המסייעים כשלעצמם להקטין את גובה העץ. אף שאינטואיטיבית אין הדבר ברור, ניתן להוכיח כי סדרת פעולות בעצים אלו חסומה גם היא, אף במקרה הגרוע ביותר, בסיבוכיות לוגריתמית.
- עצי kd
- עצים שמשמשים לחיפוש נקודות במרחב k-ממדי ומנצלים את האספקט הגאומטרי של הנתונים.
מסלולי מעבר
קיימות כמה שיטות מעבר נפוצות על עצים בינאריים.
שלוש השיטות הפשוטות והנפוצות ביותר הן:
סדר תחילי (pre-order traversal)
קריאת הקודקוד, לאחר מכן קריאת תתי העץ שלו, תחילה תת-העץ השמאלי ואחר כך הימני. בהינתן הדפסת עץ המתבססות על סדר תחילי, ניתן אף לשחזר את העץ, אם אכן הוא עומד במאפייניו של עץ חיפוש.
function visit(node) print node.value if node.left != null then visit(node.left) if node.right != null then visit(node.right)
סדר תוכי (in-order traversal)
קריאת תת-העץ השמאלי, לאחר מכן קריאת השורש (הצומת ממנו התחלנו), ולאחר מכן תת-העץ הימני.
function visit(node) if node.left != null then visit(node.left) print node.value if node.right != null then visit(node.right)
עץ הוא עץ חיפוש אם ורק אם הסדר התוכי שלו ממוין.
סדר סופי (post-order traversal)
קריאת תת-העץ השמאלי, לאחר מכן תת-העץ הימני ולאחר מכן קריאת השורש. בהינתן הדפסת עץ המתבססות על סדר סופי, ניתן אף לשחזר את העץ בצורה חד-חד ערכית, אם אכן הוא עומד במאפייניו של עץ חיפוש.
function visit(node) if node.left != null then visit(node.left) if node.right != null then visit(node.right) print node.value
בעץ חיפוש זה,
Breadth-first search (BFS)
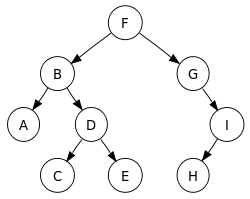
שיטה נוספת היא מעבר רוחבי על רמות העומק בעץ בזו אחר זו: F, B, G, A, D, I, C, E, H (F ראשון).
עצים לא בינאריים
קיימים כמה סוגים של עצים לא בינאריים. עצי multiway מסדר m, שבהם לכל אב יש עד m בנים (כל עץ יקבל m משלו לפי הצורך). וריאציה שלהם הם עצי B, שבהם כל העלים באותה רמה ומספר הבנים אינו נמוך לעולם ממחצית m. וריאציה נוספת היא עצי B+. בעצים אלו כל הקודקודים עד העלים אינם מכילים מידע, אלא משמשים אך ורק כמפתחות המכוונים את מסלול החיפוש.
השימוש בעצים אלו נוח כאשר חשוב לחסוך במספר החיפושים על ידי העלאת בסיס לוגריתם גובה העץ ובמקרה של עצי B+, כאשר חפצים שהעלים מכילי המידע יהיו מאוחסנים סדרתית.
סוג נוסף של עצים מאוזנים בהם הצמתים הפנימיים אינם מכילים מידע הם עצי R. עצים אלו משמשים לגישה למידע מרחבי, כלומר לנתונים עם אופי רב ממדי. נתונים כאלו יכולים להיות קואורדינטות גאוגרפיות, מלבנים וצורות גאומטריות נוספות. הרעיון העיקרי בעץ R הוא לקבץ עצמים שסמוכים זה לזה במרחב n-ממדי, ולייצג אותם ברמה גבוהה יותר בעץ על ידי מלבן חוסם מינימלי - המלבן ה-n-ממדי הקטן ביותר שמקיף אותם (ומקביל לצירים).
עץ חיפוש מסוג אחר הקרוי עץ תחיליות (או עץ חיפוש דיגיטלי) מאפשר חיפוש המתבסס על דמיון בתוך מרכיבים של שמות. העץ מסודר כך שכל מילה או מספר מפורק לרכיביו ומכל רכיב (אות, ספרה וכדומה) ניתן להמשיך לאחד הרכיבים האפשריים הבאים.
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |
קישורים חיצוניים
עץ חיפוש40399864Q623818