עקום בזייה

עקום בזייה

עקום בזייה (Bézier) הוא תיאור פרמטרי של עקום השימושי במיוחד בגרפיקה ממוחשבת. עקומי בזייה מוגדרים על ידי קבוצה של נקודות בקרה, כאשר נקודת הבקרה הראשונה והאחרונה הן קצות העקום, ויתר הנקודות לא בהכרח מצויות על העקום (ולרוב לא נמצאות עליו).

לעקומי בזייה שימושים רבים בתחומי הגרפיקה הממוחשבת. בין היתר משמשים עקומי בזייה בגרפיקה וקטורית כדי למדל עקומים חלקים שאותם ניתן להרחיב בצורה אינסופית, ובתוכנות לעריכה גרפית נעשה שימוש בצירוף של מספר עקומי בזייה כדי להגדיר מסלולים (paths).

הבסיס המתמטי לעקומי בזייה הם פולינומי ברנשטיין, שאותם פיתח המתמטיקאי הרוסי סרגיי נתנוביץ' ברנשטיין ב-1912, אולם חשיבותם הובנה רק כעבור כחצי מאה. שימוש בפולינומים אלו פותח ב-1959 על ידי Casteljau עבור שימוש של סיטרואן. שימוש נרחב בעקומים אלו נעשה בעקבות עבודתו של המהנדס הצרפתי פייר בזייה (Pierre Bézier) ב-1962 שהשתמש בהם לתכנון גוף רכב של חברת רנו.

ניתן להכליל את עקומי בזייה לממדים גבוהים יותר באמצעות משטחי בזייה.

הגדרה

עקומי בזייה מוגדרים על ידי קבוצת נקודות בקרה $P_{0},\ldots ,P_{n}$ , כאשר $n$ הוא דרגת העקום (כאשר $n=1$ העקום הוא לינארי, כאשר $n=2$ הוא ריבועי וכו').

העקום מוגדר בצורה הבאה:

${\begin{aligned}\mathbf {B} (t)&=\sum _{i=0}^{n}{\binom {n}{i}}(1-t)^{n-i}t^{i}\mathbf {P} _{i}\\&=(1-t)^{n}\mathbf {P} _{0}+{\binom {n}{1}}(1-t)^{n-1}t\mathbf {P} _{1}+\cdots \\&{}\cdots +{\binom {n}{n-1}}(1-t)t^{n-1}\mathbf {P} _{n-1}+t^{n}\mathbf {P} _{n}\ ,\ t\in [0,1]\end{aligned}}$

עקום בזייה לינארי

בהינתן שתי נקודות בקרה $\mathbf {P} _{0},\mathbf {P} _{1}$ , עקום בזייה לינארי הוא פשוט הקו הישר בין שתי הנקודות הניתן על ידי:

$\mathbf {B} (t)=\mathbf {P} _{0}+t(\mathbf {P} _{1}-\mathbf {P} _{0})=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}\ ,\ t\in [0,1]$

זה שקול לאינטרפולציה לינארית.

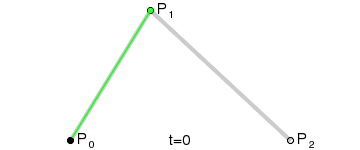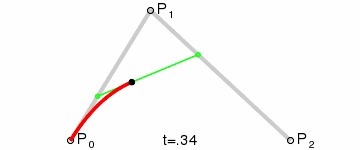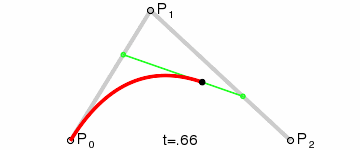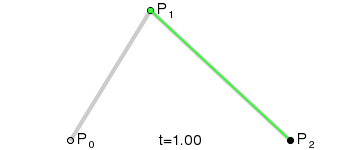
עקום בזייה ריבועי

עקום בזייה ריבועי הוא עקום המוגדר על ידי שלוש נקודות בקרה $\mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _{2}$ , ומוגדר על ידי:

$\mathbf {B} (t)=(1-t){\bigl [}(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\bigr ]}+t{\bigl [}(1-t)\mathbf {P} _{1}+t\mathbf {P} _{2}{\bigr ]}\ ,\ t\in [0,1]$

ניתן לראות בכך אינטרפולציה לינארית על הנקודות המוגדרות על ידי עקומי בזייה, המוגדרים באמצעות שתי הנקודות $\mathbf {P} _{0},\mathbf {P} _{1}$ ושתי הנקודות $\mathbf {P} _{1},\mathbf {P} _{2}$ בהתאמה.

ניתן לראות זאת בסידור מחדש של המשוואה הקודמת:

$\mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}\ ,\ t\in [0,1]$

נגזרת העקום לפי $t$ היא:

$\mathbf {B} '(t)=2(1-t)(\mathbf {P} _{1}-\mathbf {P} _{0})+2t(\mathbf {P} _{2}-\mathbf {P} _{1})$

מן הנגזרת ניתן להסיק כי המשיקים לעקום בנקודות $\mathbf {P} _{0},\mathbf {P} _{2}$ נפגשים ב-$\mathbf {P} _{1}$ . ככל ש-$t\in [0,1]$ גדל – העקום מתרחק מ- $\mathbf {P} _{0}$ לכיוון $\mathbf {P} _{1}$ , ואז מתעקם לעבר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{P}_2} מכיוון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{P}_1} .