פולימורפיזם (מדעי המחשב)

במדעי המחשב, פולימורפיזם (מאנגלית Polymorphism, בעברית: רב־צורתיות) הוא תכונה של שפות תכנות המאפשרת לכתוב קוד מופשט מבחינת הטיפוס. הקוד האבסטרקטי ירוץ בצורה שונה, בהתאם לטיפוס עליו הוא עובד. כך אפשר לכתוב פעם אחת קוד המקבל משמעויות שונות בהקשרים שונים. פולימורפיזם הוא הדרך המקובלת בעולם התוכנה לבצע הפשטה מושגית.

פולימורפיזם מהווה תכונה חשובה במתודולוגיית תכנות מונחה עצמים ובתכנות פונקציונלי. שפת תכנות התומכת בפולימורפיזם נותנת למתכנת את היכולת לממש אלגוריתמים ומבני נתונים לשימוש כללי, ולגזור מהם צורות שימוש שונות בהתאם לעצמים ולנסיבות המשתנות, באופן מפורש או מובלע.

סוגי הפולימורפיזם השונים

מבחינים בין סוגים של פולימורפיזם:

• העמסה - הגדרה של מספר פונקציות שונות בעלות אותו שם, כך שהמהדר מחליט בדרך כלשהי באיזו מהפונקציות להשתמש, על פי הטיפוס של הערכים המועברים כפרמטר. בשפות מסוימות העמסה מוגדרת עבור מספר טיפוסים קבועים מראש. דוגמה לכך היא אופרטור החיבור בשפת C, המוגדר עבור חיבור בין מספרים שלמים ובין מספרים ממשיים (4+5 או 3.2+5.4). שפות רבות מאפשרות למתכנת להגדיר העמסה באופן ידני.
• פולימורפיזם פרמטרי - היכולת לתת פרמטריזציה עבור מבנים של שפת התכנות. למשל פונקציות בשפה לא מוגדרות עבור טיפוס ספציפי, וכך מסוגלות לטפל במגוון רחב (ואינסופי) של טיפוסים שונים. פונקציות כאלה נקראות פונקציות פולימורפיות. ישנם שני סוגים של פולימורפיזם כזה:
  • Let-Polymorphism, שהדוגמה הבולטת עבורו היא פונקציות בשפת ML ובשפות פונקציונליות נוספות, כגון Haskell. הפרמטריזציה עבור פונקציות אלה איננה מפורשת, אלא אך ורק מוסקת מתוכן הפונקציה.
  • פולימורפיזם פרמטרי מפורש, כגון תבניות (Templates) בשפת ++C, וכן מבנים מסוימים בשפת ML והאסקל. בתכנות מונחה-עצמים, שימוש בפולימורפיזם פרמטרי נקרא תכנות גנרי. פולימורפיזם כזה, במימוש אידיאלי, ממומש על פי רוב בזמן הידור.
• פולימורפיזם של תת-טיפוס (או פולימורפיזם הכלה) ממומש על פי רוב בשפות תכנות מונחות-עצמים. מושג זה מתורת הטיפוסים אומר שמזהה עשוי להתייחס למופע השייך למספר כלשהו של מחלקות, כל עוד הן חולקות ביניהן מחלקת אם משותפת. פולימורפיזם כזה מנצל את היכולת לבצע חיפוש דינמי בזמן ריצה, ובביצוע דריסה של מתודות.
• Type Coercion - המרה אוטומטית ומובלעת בין טיפוסים. דוגמה להמרה כזאת היא ההרחבה של המספר 4 ממספר שלם למספר ממשי בביטוי 4+5.2 (בשפות התכנות המאפשרות כתיבה של ביטוי כזה). ניתן להראות שהמרה כזאת היא שקולה לפולימורפיזם של תת-טיפוסים (ירושה), ואכן, שפת D משתמשת במנגנון הזה כדרך לדמות ירושה מרובה.

הרעיון הבסיסי

בהינתן אלגוריתם מסוים, למשל אלגוריתם למיון מערך, אין דרישה בסיסית באלגוריתם לדעת כל פרט על הטיפוס של אברי המערך. כל שיש לדעת הוא את גודל המערך, כיצד ניתן לבצע השוואה בין איברי המערך, וכיצד ניתן לשנות את הסדר שלהם. בשפות תכנות בעלות טיפוסיות חזקה וסטטית, שמקפידות על סוג המשתנה שמועבר לפרוצדורה, זו עשויה להיות בעיה: בכתיבת פרוצדורה שתמיין את איברי המערך, מאיזה טיפוס נגדיר את הפרמטרים שלה? יש צורך למצוא דרך להגדיר טיפוס מסוג גנרי כלשהו, שכל הידוע עליו הוא הנתונים החיוניים למימוש הפרוצדורה, ותו לא. ישנן שפות שמאפשרות זאת באמצעות מנגנון לזיהוי אוטומטי של הטיפוס של כל ביטוי (כמו שפת התכנות ML), באמצעות טכניקות של ירושה ודריסה בתכנות מונחה עצמים, או באמצעות תכנות גנרי. כמו כן, כל שפה בעלת מערכת טיפוסים חלשה או דינמית, כגון פייתון, מאפשרת פולימורפיזם.

פולימורפיזם אד-הוק

העמסה (Overloading)

פולימורפיזם בצורתו הבסיסית ביותר קיים בכל שפת תכנות עילית. כאשר כותבים ביטויים כגון (4 + 4) או (5.3 + 2.1), אנו מנצלים את העובדה שאופרטור החיבור מועמס - כלומר, בעל משמעות כפולה - גם לטיפוס המשמש למספרים שלמים כמו 4, וגם לטיפוס המשמש לייצוג מספרים ממשיים כמו 2.1; זאת, אף על פי שהייצוג של מספרים אלו כביטים בשפת המכונה שונה לחלוטין בין מספרים שלמים למספרים ממשיים, ולכן גם פקודות המכונה המורות למעבד לבצע את פעולת החיבור תהיינה שונות; כל זה שקוף למתכנת, ולכן מקל על עבודתו.

המרה (Coercion)

שפת C מאפשרת צורה מוגבלת מאוד של פולימורפיזם, נוסף על העמסה בסיסית של אופרטורים אריתמטיים: בשפה מוגדרת המרה אוטומטית מכל טיפוס של מצביע אל הטיפוס הגנרי *void, ובחזרה. מנגנון זה מנוצל על ידי פונקציות כגון פונקציית הספרייה הסטנדרטית qsort המשמשת למיון מערך, המקבלת מערך של מצביעים וממיינת אותו, תוך התייחסות אל כל המצביעים במערך כ-*void. טכניקה זו מאפשרת לבצע כל פעולה, אך היא איננה גמישה, ומצריכה מידע מפורש מהמתכנת בקשר לגודל של משתנים מהטיפוס שמועבר בפועל - מידע שאמור להימצא בידי המהדר בזמן הידור התוכנית, ולכן דורשת עבודה מיותרת. שפות אחרות, כגון שפת פסקל, לעיתים אינן מאפשרות אפילו גנריות בסיסית כזאת.

פולימורפיזם פרמטרי

שפת C

ניתן לבצע פולימורפיזם בעזרת פקודות מאקרו, שמבצעות החלפה של טקסט מסוים בתוכנית בטקסט אחר, לפני ההידור. לדוגמה, המאקרו הבא בשפת C :

#define min(x,y) ( ((x) < (y)) ? (x) : (y) )

מדמה פונקציה שמחזירה את המינימום מבין הביטויים המועברים אליה, ומתאימה לכל טיפוס עליו מוגדרת פעולת ההשוואה ">" (פעולה שבפני עצמה מועמסת, בדומה לאופרטור החיבור, ולכן פולימורפית). עם זאת, למאקרו כזה ישנם חסרונות רבים לעומת פונקציה אמיתית: לא מתבצעת בדיקת טיפוסים, ביטוי עם תוצאת לוואי עלול לבצע אותה מספר פעמים, ולהחזיר תוצאה לא צפויה, ועוד.

שפת ++C

בשפת ++C‏, פולימורפיזם פרמטרי ממומש בזמן הידור, תוך שימוש בתבניות (templates):

template <typename T>
T max(T x, T y)
{
 return x < y ? y : x;
}

התבנית הזאת מגדירה משפחה של פונקציות max המקבלות שני איברים מסוג כלשהו, ומספר איברים ראשונים, ומחזירות את הגדול מביניהם. הדרישות היחידות על הטיפוס של המערך הן שניתן לבצע השוואה בין שני איברים באמצעות האופרטור '>', ושניתן לבצע העתקה של איבר. לכן ניתן להעביר כפרמטרים שני ערכים מטיפוס int, או double, או של מחלקה שהגדיר המשתמש ושמממשת את האופרטור '>'.

במקרה זה, בכל קריאה לפונקציה max יבדוק המהדר אם כבר הוגדרה פונקציה כזאת עבור הטיפוס המסוים המופיע בקריאה, ואם לא הוא ייצור פונקציה חדשה שהיא מופע של התבנית שהגדרנו.

ספריית התבניות התקנית של שפת ++C היא דוגמה לתכנות גנרי, ומבוססת ברובה על פולימורפיזם פרמטרי ושימוש בתבניות.

שפת עדה מאפשרת אף היא תכנות גנרי באופן דומה לתבניות של ++C.

שפת ML

בשפת ML, התומכת בפולימורפיזם מלא ומתוחכם, הדבר מתבצע כך: המתכנת כותב פונקציה, למשל פונקציה שהופכת רשימה, בדרך הטבעית לו, ללא הצהרה על הטיפוס אותו הפונקציה מקבלת. המהדר של השפה מסיק לבד, על פי הביטויים המשמשים בפונקציה, אילו טיפוסים ניתן להעביר אליה. טיפוסים אלה עשויים להיות קונקרטיים, כגון int שהוא מספר שלם, או גנריים, ואז הם יסומנו בתג ושם, למשל a' - זה בעצם "משתנה טיפוס" (type variable). המנגנון ידרוש עקביות: אם פונקציה מקבל שני ארגומנטים מטיפוס a', ניתן להעביר אליה שני משתנים שהם מספר שלם או שני משתנים שהם מספר ממשי, אך לעולם לא משתנה אחד ממשי ואחד שלם, כיוון ששני הארגומנטים חייבים להיות מאותו טיפוס.

דוגמה לפונקציה פולימורפית בשפת ML:

fun f x = [x,x,x];

פונקציה זאת מקבל ערך x מכל טיפוס שהוא, ומחזירה רשימה של שלושה איברים שערכם x. הטיפוס של הפונקציה הוא "פונקציה מטיפוס a אל רשימה של a". בניגוד לתבניות של שפת ++C פונקציה פולימורפית היא פונקציה לכל דבר.

גם שפת Haskell תומכת בפולימורפיזם פרמטרי באופן דומה, ואף נרחב יותר.

שפת ג'אווה

בשפות ג'אווה יש מתודות גנריות (החל מגרסה 7 ואילך), אך בדומה למחלקות גנריות בג'אווה, המידע לגבי הטיפוסים משמש רק לבדיקה בזמן קומפילציה ואיננו קיים בזמן ריצה, כך שזהו למעשה פולימורפיזם של הכלה (תת-טיפוסים) הנבדק בזמן הידור.

שפת #C

בשפת C# ישנן מתודות גנריות.

פולימורפיזם של תת-טיפוסים

שפות תכנות התומכות בפולימורפיזם מאפשרות להגדיר מושגים כלליים ולגזור מהם מקרים ספציפיים יותר. בנוסף, מאפשרת השפה להתייחס למושג בצורה מופשטת. התייחסות למושג בצורה מופשטת, מאפשרת להשתמש בקוד כללי הפועל על סוגים רבים ושונים של מושגים דומים לו. למעשה, ניתן להשתמש בקוד המתאים לעצם הכל טיפוס המהווה מקרה פרטי של המושג הכללי.

למשל, אף שיש מרחק רב בין מנוע של מעבורת חלל לבין מנוע של מכסחת דשא, באמצעות קונספט זה שיש בו הפשטה מושגית (מנוע יוגדר כמכונה הממירה אנרגיה לעבודה מכנית), אפשר להתייחס אליהם ואל מגוון האפשרויות שביניהם (מנועים של מטוס קרב סילוני, מטוס בואינג, מטוס קל, אוניה, טנק, משאית, מכונית, אופנוע, קטנוע), מתוך מחלקה תכנותית אחת, תוך ביצוע התאמות לכל אחד מהמנועים על פי המאפיינים הייחודיים שלו. גישה זו שיוצאת מהאבסטרקט ומגיע אל הקונקרטי ביותר (למשל בתיאור מפורט ומלא של מנוע מכונית מדגם מזדה 3), מונעת את הצורך לכתוב מחדש מחלקות נפרדות, עבור כל אחד ואחד מטיפוסי המנועים השונים, והיישומים המעשיים של כל אחד ואחד מהם (שהרי יש מנועי 4 פעימות של חברות שונות), ומסירה מהתכנות את הסרבול של הכתיבה החוזרת ונשנית ובכך הופכת אותו לריכוזי, יעיל ואלגנטי.

בשפת C# אפשר לבצע פולימורפיזם של תת-טיפוס בכמה דרכים: באמצעות שיטות וירטואליות, באמצעות ממשקים ובאמצעות מחלקה אבסטרקטית.

מנגנונים הרווחים ברב צורתיות

מנגנונים הרווחים ברב צורתיות, הם:

• דריסה (Override) שבה ניתן להחליף פונקציה של מחלקת בסיס בפונקציה שונה במחלקה הנגזרת ממנה. באמצעות מנגנון זה ניתן להתאים את הפעולה לסוג המיוחד של האובייקט. שם הפעולה נשמר והיא מתבצעת בדרכים שונות בהתאם לאובייקט אליו היא מתייחסת. טכניקה נוספת היא הצללה שדומה ליכולת הדריסה.
• העמסת אופרטורים (Operator Overloading), היא מקרה פרטי של העמסת פונקציות, שבו אופרטור מסוים מקבל מכניזם פנימי שונה בתוך אובייקט. למשל אופרטור + שנועד לחבר מספרים, במחלקה של מחרוזות מקבל יכולת שרשור, ובמחלקה של מערכים יכול לקבל יכולת לחבר בין שני מערכים.

דוגמאות

כדי להדגים את הכוח של המנגנון, אפשר לחשוב על דוגמה שכיחה מחיי היום יום, אלגוריתם להחלפת גלגל ברכב:

1. עצרו בצד והציבו סימנים המיידעים שהרכב בטיפול.
2. הציבו את המגבה במקומו ושחררו מעט את בורגי הגלגל.
3. הגביהו את הרכב בעזרת המגבה.
4. פרקו את הגלגל והרכיבו במקומו גלגל תקין.
5. חזקו מעט את הברגים.
6. הנמיכו את הרכב עד שהגלגל יגע קלות בקרקע.
7. חזקו את בורגי הגלגל בהצלבה.
8. הנמיכו את הרכב, איספו את הכלים והמשיכו בנסיעה.

האלגוריתם, כפי שתואר, מתאים לכל סוג רכב, לאוטובוסים ומשאיות וגם למכוניות קטנות. כמעט כל פעולה המתוארת באלגוריתם תבוצע בצורה שונה בכל סוג רכב. הפעלת מגבה של אוטובוס, לדוגמה, שונה מאוד מהפעלת מגבה של מכונית קטנה. העובדה שהצלחנו לנסח אלגוריתם כללי (גנרי) לכל כלי הרכב אף על פי שבעצם בכל רכב האלגוריתם הוא אחר היא בזכות ההתייחסות המופשטת שלנו לרכב. בזמן שניסחנו את האלגוריתם לא התעניינו באיזה רכב מדובר אלא דיברנו על רכב כלשהו. כל דבר שאמרנו על רכב, דאגנו שיהיה נכון לכל רכב. לדוגמה, אמרנו "חזקו מעט את הברגים" ולא אמרנו "חזקו מעט את ארבעת הברגים".

אלגוריתם זה נכתב פעם אחת ומופעל פעמים רבות על כלי-רכב שונים. בכל פעם האלגוריתם מקבל צורה אחרת, בהתאם לסוג הרכב. ללא מנגנון הפולימורפיזם היה צריך לכתוב את האלגוריתמים הספציפיים עבור כל סוגי כלי-הרכב ולא ניתן היה למצות את המכנה המשותף של כולם.

דוגמה נוספת, מתחום המתמטיקה: אלגוריתם למציאת בסיס אורתונורמלי במרחב מכפלה פנימית (תהליך גרם שמידט). כאשר נתון בסיס קיים:

1. בחרו וקטור כלשהו ונרמלו אותו.
2. בחרו וקטור נוסף והטילו אותו על תת-המרחב הנפרש על ידי הווקטורים שכבר בחרתם.
3. מצאו את ההפרש בין הווקטור להטלה שלו, נרמלו אותו והוסיפו אותו לרשימת הווקטורים שכבר נבחרו.
4. חיזרו על הפעולות 2 ו-3 עד שיגמרו הווקטורים בבסיס המקורי. רשימת הווקטורים שנבחרו מהווה בסיס אורתונורמלי למרחב.

כדי להיות וקטור יש למלא סט קצר של דרישות שיכול להתמלא על ידי אובייקטים מתמטיים שונים מאוד זה מזה. מכפלה פנימית גם היא יכולה להיות מוגדרת בדרכים רבות מאוד בעלות משמעויות שונות. הוכחת נכונות האלגוריתם מסתמכת רק על סט התכונות שמקיימים כל וקטור וכל מכפלה פנימית ולכן היא תקפה תמיד.

מימוש בתכנות

פולימורפיזם יכול להיות ממומש בזמן ריצה או בזמן הידור. ב- C++‎ ממומש פולימורפיזם של זמן ריצה על ידי מצביע מסוג מופשט, המצביע לאובייקט קונקרטי. הקוד הבא מדגים איך ניתן לעשות זאת:

 class Car {...};

 class Bus: public Car{...};

 class PrivateCar: public Car{...};

 void changeWheel(Car *p) {
 p->stop();
 p->placeJack();
 p->lift();
 ...
 }

 int main() {
 Car* array[3];
 array[0]=new Bus();
 array[1]=new PrivateCar();
 array[2]=new Bus();
 for(int i=0;i<3; ++i)
 changeWheel(array[i]);
 }

בדוגמה זו, הפונקציה changeWheel משתמשת במנגנון הפולימורפיזם על מנת לתאר את אופן החלפת הגלגל במכונית כלשהי.

הפונקציה מקבלת מצביע למכונית כללית. למעשה מדובר בסוג מסוים של מכונית, מכונית ספציפית, אבל changeWheel מתייחסת אליה פשוט כמכונית ומבצעת עליה רק פעולות שאפשר לעשות על כל מכונית. כאשר changeWheel תבקש ממכונית לעשות פעולה מסוימת, המכונית תבצע את הפעולה באופן ייחודי לה. ניתן לראות שהממשק למכונית מוגדר על ידי ההתייחסות המופשטת (המצביע למכונית כללית) ואילו הפעולה שתתבצע למעשה מוגדרת על ידי הטיפוס הספציפי (סוג המכונית).

כל הדברים הללו מתאימים לאופן שבו אנו משתמשים באבסטרקציה בחיי היום יום. נחשוב לדוגמה על המשפט: "בחדר ההמתנה צריך לשים מספר כיסאות בשביל שהלקוחות לא יצטרכו לחכות בעמידה". המשפט משתמש במושג המופשט "כיסא". יש המון סוגי כיסאות אבל המשפט מתייחס רק לתכונה המשותפת של כולם: כיסא מאפשר לשבת. כאשר המשפט ייושם, ייבחרו סוגים ספציפיים של כיסאות. אולי יהיו להם ארבע רגליים ואולי שלוש, אבל בכל מקרה הם יאפשרו ללקוחות להמתין בישיבה.

גם בדוגמה זו השתמשנו בהתייחסות מופשטת, התנסחנו באופן כללי שאיננו תלוי בסוג הספציפי ולבסוף ראינו איך הטענות הכלליות מקבלות משמעות ספציפית בהתאם לסוג שבו מדובר.

הפעלת אלגוריתם כללי על מבנה נתונים הטרוגני ניתנת לביצוע על ידי פולימורפיזם בזמן ריצה ולא ניתנת לביצוע על ידי פולימורפיזם בזמן הידור. לדוגמה מערך המכוניות שהופיע בדוגמה הראשונה, מכיל מכוניות מסוגים שונים, כלומר מדובר במערך הטרוגני ולא הומוגני. בדוגמת הקוד השנייה היינו יכולים להפעיל את הפונקציה הפולימורפית רק על מערך הומוגני של מכוניות.

מימוש פולימורפיזם על ידי המהדר

נתבונן שוב בקטע הקוד המממש פולימורפיזם בזמן ריצה:

void changeWheel(Car *p) {
 p->stop();
 p->placeJack();
 p->lift();
 ...
}

נשאלת השאלה כיצד מתורגם קטע זה לשפת מכונה. לדוגמה הפעלת הפונקציה stop:

p->stop();

בניגוד להפעלת פונקציה רגילה, בזמן ההידור לא ידוע איזה קוד יש להפעיל. האם מדובר ב -() Bus::stop ,ב -() PrivateCar::stop או אולי פונקציית stop של טיפוס אחר. התשובה לשאלה זו מתבררת רק בזמן ריצה, כאשר ידוע על איזה טיפוס ספציפי מצביע p. הקומפיילר, אם כן, צריך לייצר קוד הקורא לפונקציה מסוימת בהתאם לטיפוס האובייקט שמוצבע על ידי p באותו הרגע. כדי לייצר קוד כזה, יש להתייחס לקוד הנמצא בכתובת משתנה. במילים אחרות יש להשתמש במושג של מצביע לפונקציה.

הקוד הבא מדגים איך אפשר לממש פולימורפיזם בשפת C, שפה שלא תומכת בפולימורפיזם באופן מובנה:

 #include <malloc.h>
 #include <stdio.h>

 typedef void (*fun_t)(void);

 typedef struct Car {
 fun_t stop;
 /* fun_t placeJack, lift, ... */
 } Car;

 Car* createCar(fun_t stopFunction) {/*fun_t placeJackFunction, fun_t liftFunction,...*/
 Car *p = (Car*)malloc(sizeof(Car));
 p->stop = stopFunction;
 /* p->placeJack = placeJackFunction; p->lift = ... */
 return p;
 }

 void busStop() { printf("Stopping the bus...\n"); }
 /* void busPlaceJack() {...} void busLift() {...} ... */
 Car* createBus() { return createCar(busStop); }

 void privateStop() { printf("Stopping the private car...\n"); }
 /* void privatePlaceJack() {...} void privateLift() {...} ... */
 Car* createPrivate() { return createCar(privateStop); }

 void changeWheel(Car *car) {
 car->stop();
 /* car->placeJack(); car->lift();... */
 }

 int main() {
 Car *p1 = createBus(), *p2 = createPrivate();
 changeWheel(p1);
 changeWheel(p2);
 /* free memory .. */
 return 0;
 }

הדוגמה האחרונה פשטנית במקצת. היא מתחמקת מבעיות טכניות שונות המופיעות באובייקטים פחות מנוונים מאלה שבדוגמה. בנוסף, ניתן לראות שהשיטה המוצגת בדוגמה, בזבזנית בזיכרון. עבור כל אובייקט (מכונית) יש לשמור מספר מצביעים לפונקציות כמספר הפונקציות שיש למכונית. אותם מצביעים לפונקציות יכולים להוות את רוב הזיכרון הדרוש לאחסון האובייקט. בזבוז הזיכרון נובע מהעובדה, שאוסף הפונקציות עליהם מצביע האובייקט הוא מאפיין של ה - class ולא של האובייקט הספציפי. לדוגמה, לכל האובייקטים מסוג Bus יהיו בדיוק אותם ערכים בכל מצביעי הפונקציות שלהם.

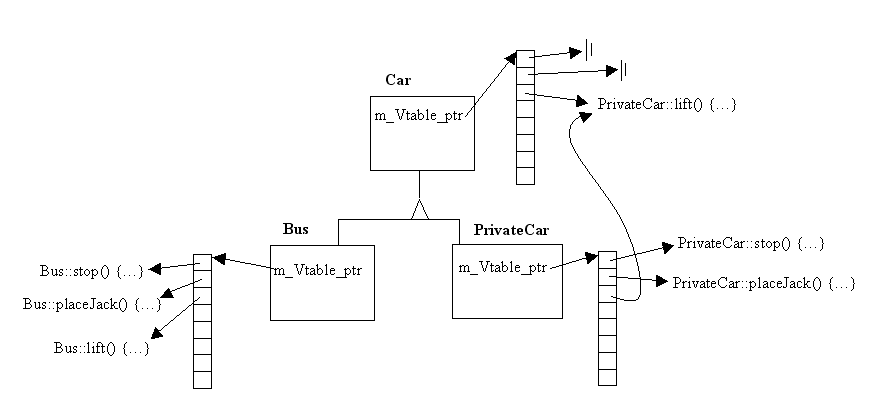
בגלל העובדה שמדובר בעצם במידע של ה-class, הגיוני לצמצם את כל מצביעי הפונקציות למצביע יחיד שיפנה למקום בו נמצאת כל האינפורמציה של ה-class. האינפורמציה הזו יכולה להיות פשוט מערך של מצביעים לפונקציות - אותם מצביעים שתוארו בדוגמה והוו שדות באובייקט. הרעיון שתואר הוא באמת השיטה המקובלת לממש פולימורפיזם של זמן ריצה. אותו מערך פונקציות נקרא virtual table ואותו שדה יחיד המצביע עליה נקרא virtual table pointer.

כפי שניתן לראות בתמונה, כל אובייקט מסוג Car או מסוג היורש מ-Car, מחזיק מצביע לטבלה ייעודית לאותו סוג. הטבלה מחזיקה מצביעים לפונקציות. הקוד

 p1.placeJack()

יתורגם לקוד הדומה לקוד הבא:

 p1.m_vtbl_ptr[2]()

כפי שניתן לראות, קיימת כאן הסתמכות על העובדה שהפונקציה placeJack נמצאת תמיד באותו אינדקס, בכל הטבלאות הווירטואליות (במקרה זה - 2).

מחיר פולימורפיזם הממומש על ידי virtual table

מבחינת זיכרון, כאשר ל-Class יש לפחות פונקציה פולימורפית (וירטואלית) אחת, כל אובייקט מסוגו (ומסוג יורשיו) יכיל מצביע virtual table pointer. עבור אובייקטים גדולים הדבר עשוי להיות זניח אבל עבור אובייקטים קטנים, במיוחד אם יש מופעים רבים שלהם, הדבר עלול להיות משמעותי.

מבחינת זמן הריצה המחיר הוא מעבר אחד דרך תא של מערך הטבלה הווירטואלית. בדרך כלל הדבר מתורגם לפקודות בודדות בשפת מכונה (במקרים רבים - פקודה בודדת). לרוב, התשלום בזמן הריצה הוא זניח אבל במקרים בהם הפונקציה הווירטואלית קצרה מאוד והיא נקראת מספר רב של פעמים - המחיר עלול להיות משמעותי.

באופן כללי, השימוש בפונקציות פולימורפיות נחשב לטכניקה יעילה.

לקריאה נוספת

• John C. Mitchell, Concepts In Programming Languages, Cambridge University Press, 2003 פרק 6
• David A. Watt, Programming Language Concepts and Paradigms, פרק 7

קישורים חיצוניים

• אורי מוסינזון, הרצאה על פולימורפיזם בתכנות מונחה-עצמים, במסגרת קורס שניתן באוניברסיטה העברית, באתר האוניברסיטה
• Object-oriented programming concepts: Polymorphism and interfaces, באתר אדובי מערכות

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

38540810פולימורפיזם (מדעי המחשב)