סדרה הנדסית אינסופית מתכנסת

סדרה הנדסית אינסופית מתכנסת היא מקרה פרטי של הסדרה ההנדסית, כאשר מנתה $- 1 < q < 1$ או $| q | < 1$ .

סדרה הנדסית שלא מקיימת תנאי זה נקראת סדרה הנדסית מתבדרת.

הוכחת נוסחת הסכום

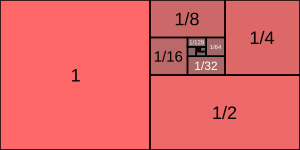
נתונה הסדרה ההנדסית האינסופית המתכנסת $a_{1}, a_{2}, a_{3}, a_{4}, \dots$ שמנתה $| q | < 1$ .

נוסחת הסכום של סדרה הנדסית: $S_{n} = \frac{a_{1} (q^{n} - 1)}{q - 1}$

נחשב את הגבול של סכום הסדרה כאשר $n$ שואף ל- $\infty$ :

\lim_{n \to \infty} S_{n} = \lim_{n \to \infty} \frac{a_{1} (q^{n} - 1)}{q - 1} = \frac{a_{1} (\lim_{n \to \infty} q^{n} - 1)}{q - 1} = \frac{a_{1} (0 - 1)}{q - 1} = \frac{a_{1} (- 1)}{q - 1} = \frac{a_{1}}{1 - q}

כדאי לשים לב שמכיוון שמתקיים $| q | < 1$ אז $\lim_{n \to \infty} q^{n} = 0$ .

את סכום הסדרה ההנדסית המתכנסת ניתן לכתוב כ- $S_{\infty}$ או בצורה הנפוצה יותר $S$ .

נתונה סדרה הנדסית שבה $a_{1} = 1, q = \frac{1}{2}$ . נחשב את המספר אליו הסכום שלה מתכנס: $S = \frac{1}{1 - \frac{1}{2}} = \frac{1}{\frac{1}{2}} = 2$