משפט צ'בה

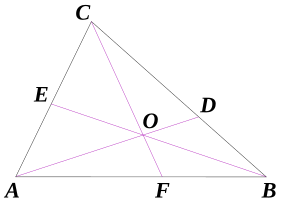
בגאומטריה האוקלידית, משפט צ'בה קובע שאם מחברים כל קודקוד במשולש לנקודה על הצלע שמולו, ושלושת הקטעים נפגשים בנקודה, אז מכפלת יחסי החלוקה היא 1; ולהפך - אם מכפלת יחסי החלוקה היא 1, אז הקטעים נפגשים בנקודה. במשפט זה, יחס החלוקה מחושב עם סימן, והוא נכון גם לגבי חלוקה חיצונית. עבור הישרים AD, BE ו-CF (ראו ציור), המכפלה היא $\frac{A F}{F B} \cdot \frac{B D}{C D} \cdot \frac{C E}{E A} = 1$ .

ניסוח נוסף של המשפט המשתמש בזוויות, המכונה "משפט צ'בה הזוויתי" הוא:

\frac{\sin ∠ B A D}{\sin ∠ C A D} \cdot \frac{\sin ∠ A C F}{\sin ∠ B C F} \cdot \frac{\sin ∠ C B E}{\sin ∠ A B E} = 1 .

ניתן להוכיח שהניסוחים שקולים בעזרת שימוש במשפט הסינוסים.

העובדה ששלושת התיכונים במשולש נפגשים בנקודה היא מקרה פרטי, שבו כל היחסים שווים לאחד.

הוכחה

יש למשפט כמה וכמה הוכחות גאומטריות, אבל ההוכחה בשיטות של גאומטריה אנליטית היא כנראה הפשוטה מכולן. מכיוון שהנקודות A,B,C אינן על קו ישר אחד, כל נקודה במישור, ובפרט O (ראו ציור) היא ממוצע משוקלל שלהן, כלומר, קיימים משקלים $α, β, γ$ , שסכומם 1, כך שמתקיים: $α A + β B + γ C = O$ .

מכיוון שהנקודה D נמצאת על ישר אחד עם O ו-A, ועל ישר אחר עם B ו-C, מתקיים: $D = \frac{β}{β + γ} B + \frac{γ}{β + γ} C$ . לכן $\frac{B D}{C D} = \frac{γ}{β}$ , ובאופן דומה, $\frac{A F}{F B} = \frac{β}{α}$ , ו- $\frac{C E}{E A} = \frac{α}{γ}$ . כלומר, טענת המשפט היא ש- $\frac{β}{α} \cdot \frac{γ}{β} \cdot \frac{α}{γ} = 1$ , והטענה הזו טריוויאלית.