משפט הסינוסים

בטריגונומטריה, משפט הסינוסים קובע כי היחס בין אורך צלע במשולש כללי לבין סינוס הזווית שמולה, שווה לקוטר המעגל החוסם את המשולש: אם a,b,c הם אורכי הצלעות ו- $\alpha ,\beta ,\gamma$ הזויות שמולן, בהתאמה, אז $\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }=2R$ כאשר R הוא רדיוס המעגל החוסם.

הוכחה

א

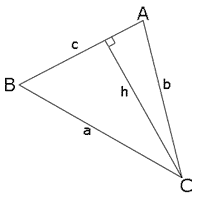
גובה המשולש המסומן ב - $h$ ניתן להצגה באופן הבא:

$h=b\sin \alpha$

אבל גם באופן הזה:

$h=a\sin \beta$

ולכן:

$b\sin \alpha =a\sin \beta$

או

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }$

מאחר שזה נכון ל-2 זוויות שנבחרו באופן שרירותי, זה נכון לכל זוג זוויות במשולש.

כאשר המשולש קהה-זווית, תהליך ההוכחה כולל שלב ביניים לפי הזווית המשלימה לזווית הקהה ולאחר מכן חוזרים לזווית הקהה עצמה על פי הזהות $\sin \alpha =\sin (180-\alpha )$. כאשר המשולש ישר-זווית המשפט הוא פשוט הגדרת הסינוס.

ב

אם מרכז המעגל החוסם הוא O, נמשיך את BO עד שהוא נפגש עם המעגל ונקרא לנקודת החיתוך D.

נתבונן במשולש BDC. במשולש ישר-זווית זה (זווית ההיקפית BCD היא בת 90 מעלות בגלל שהיא נשענת על קוטרו של המעגל). נסמן ב -$\delta$ את הזווית CDB ואז

$a=2R\sin \delta$

אבל זווית $\delta$ שווה לזווית $\alpha$ כי הן נשענות על אותה קשת, לכן

$a=2R\sin \alpha$

או

$\frac{a}{\sin \alpha }=2R$

כנדרש.

נשים לב שמהחלק השני של ההוכחה נובע בנקל החלק הראשון של הטענה

$\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }$

שכן הבחירה בצלע a ובזווית שמולה $\alpha$ הייתה שרירותית ויכולנו באותה מידה לבחור בצלע b ובזווית שמולה $\beta$.

ראו גם

• משפט הקוסינוסים
• משפט הטנגנסים

קישורים חיצוניים

• גדי אלכסנדרוביץ', מה בעצם הולך בטריגונומטריה בתיכון? (חלק ד' - משפט הסינוסים), באתר "לא מדויק", 26 ביוני 2021
• משפט הסינוסים, באתר MathWorld (באנגלית)
• משפט הסינוסים, באתר אנציקלופדיה בריטניקה (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

משפט הסינוסים40092401Q170181