הפוליום של דקארט

בגיאומטריה, הפוליום של דקארט (בלָטִינִית ׳folium׳, עלה; על שם רנה דקארט) היא עקומה אלגברית המוגדרת על ידי המשוואה הסתומה$$x^{3}+y^{3}-3axy=0.$$

הפוליום של דקארט (ירוק) עם אסימפטוטה (כחול) כאשר $a=1$

היסטוריה

העקומה הוצעה ונחקרה לראשונה על ידי רנה דקארט בשנת 1638. הסיבה לפרסומה נעוצה במקרה שהתרחש במהלך הפיתוח של החשבון האינפיניטסימלי. דקארט אתגר את פייר דה פרמה למצוא את קו המשיק לעקומה בנקודה שרירותית, שכן פרמה גילה לפני כן שיטה למציאת קווים משיקים. פרמה פתר את הבעיה בקלות, מה שדקארט עצמו לא הצליח לעשות. מאז המצאת החשבון האינפיניטסימלי, ניתן למצוא את השיפוע של קו המשיק בקלות באמצעות הצגה סתומה.

גרף של העקומה

הפוליום של דקארט בקואורדינטות קוטביות

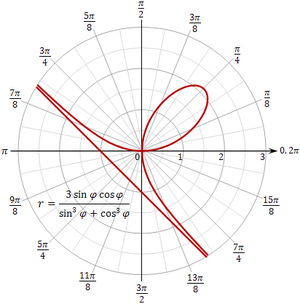
ניתן לבטא את הפוליום של דקארט בקואורדינטות קוטביות באופן הבא$$r={\frac {3a\sin \theta \cos \theta }{\sin ^{3}\theta +\cos ^{3}\theta }},$$שמשורטט בצד ימין. זה שווה ערך ל -

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = \frac{3a \sec\theta \tan\theta}{1 + \tan^3 \theta}.}

טכניקה נוספת היא כתיבה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = px} ופתירה עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} ו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} במונחים של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} . זה מניב את המשוואות הפרמטריות הרציונליות:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = {{3ap} \over {1 + p^3}},\, y = {{3ap^2} \over {1 + p^3}}} .

אנו יכולים לראות שהפרמטר קשור למיקום על העקומה באופן הבא:

• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle p < - 1} מתאים ל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>0} , הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y<0}  : ה"כנף" הימנית התחתונה.
• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1 < p < 0} מתאים ל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<0} , הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y>0}  : ה"כנף" השמאלית העליונה.
• הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle p>0} מתאים ל $x>0$, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y>0}  : הלולאה של העקומה.

דרך נוספת לשרטט את הפונקציה יכולה לנבוע מסימטריה מעל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = x} . ניתן לראות את הסימטריה ישירות מהמשוואה שלה (ניתן להחליף בין x ו-y). על ידי החלת סיבוב של 45° CW למשל, אפשר לשרטט את הפונקציה באופן סימטרי על ציר הסיבוב x.

פעולה זו מקבילה להחלפה:הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = {{u+v} \over {\sqrt{2}}},\, y = {{u-v} \over {\sqrt{2}}} } ותניבהפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v = \pm u\sqrt{\frac{3a \sqrt{2} - 2u}{6u + 3a \sqrt{2}}} } שרטוט במערכת הקרטזית של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u,v)} נותן את הפוליום מסובב ב-45° ולכן הוא סימטרי על ציר ה - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} .

תכונות

הוא יוצר לולאה ברביע הראשון עם נקודה כפולה במקור ובאסימפטוטההפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x + y + a = 0 \,.} זה סימטרי גם לגבי הקו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = x} . ככזה, השניים מצטלבים במקור ובנקודה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3a/2,3a/2)} .

ביצוע גזירה באופן סתום נותן את הנוסחה עבור השיפוע של קו המשיק לעקומה זו:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx} = \frac{ay - x^2}{y^2 - ax}}

באמצעות כל אחד מהייצוגים הקוטביים שלמעלה, שטח הפנים של הלולאה הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3a^2/2} . יתר על כן, השטח שבין "כנפי" העקומה לאסימפטוטה המלוכסנת שלה הוא גם כן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3a^2 / 2} .

הקשר לטריסקטריקס של מקלורין

הטריסקוטריקס של מקלורין

ה-folium של דקארט קשור ל-trisectrix של Maclaurin על ידי טרנספורמציה אפינית. כדי לראות זאת, יש להתחיל עם המשוואההפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3 + y^3 = 3 a x y \,,} ולשנות משתנים כדי למצוא את המשוואה במערכת קואורדינטות המסובבת 45 מעלות. זה מסתכם להגדרההפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = {{X+Y} \over \sqrt{2}}, y = {{X-Y} \over \sqrt{2}}.} בתוך המישור $X,Y$ המשוואה היאהפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2X(X^2 + 3Y^2) = 3 \sqrt{2}a(X^2-Y^2).} אם נמתח את העקומה בכיוון ה - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} לפי גורם של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{3}} נקבלהפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2X(X^2 + Y^2) = a \sqrt{2}(3X^2-Y^2),} שהיא משוואת הטריסקטריקס של מקלורין.

לקריאה נוספת

• J. Dennis Lawrence: A catalog of special plane curves, 1972, Dover Publications.מסת"ב 0-486-60288-5ISBN 0-486-60288-5, עמ'. 106–108
• George F. Simmons : Calculus Gems: Brief Lives and Memorable Mathematics, ניו יורק 1992, McGraw-Hill, xiv,355.מסת"ב 0-07-057566-5ISBN 0-07-057566-5 ; מהדורה חדשה 2007, האגודה המתמטית של אמריקה ( MAA )

קישורים חיצוניים

• Weisstein, Eric W. "Folium of Descartes". MathWorld.
• "Folium of Descartes" at MacTutor's Famous Curves Index
• "Cartesian Folium" at MathCurve
• הפוליום של דקארט, באתר MathWorld (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

הפוליום של דקארט36087386Q837771