מעגל נושק

מעגל נושק

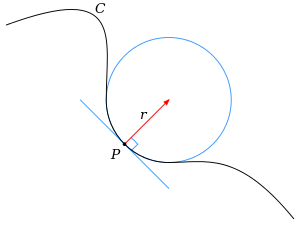
בגאומטריה דיפרנציאלית ובחקר של עקומים, מעגל נושק (Osculating circle) של עקום חלק מספיק בנקודה נתונה $P$ על העקום מוגדר כמעגל אשר מתקרב לעקום בצורה המרבית מבין כל המעגלים המשיקים (Tangent circles) לו בנקודה זו.

באופן אינטואיטיבי ניתן לתארו בתור המעגל העובר דרך $P$ ודרך שתי נקודות נוספות על העקום הקרובות אינפיניטסימלית ל-$P$ . מרכזו נח על חלקו הפנימי של הנורמל של העקום בנקודה זו, ועקמומיותו זהה לזו של העקום בנקודה זו. מרכזו ורדיוסו של המעגל הנושק נקראים בהתאמה מרכז העקמומיות ורדיוס העקמומיות של העקום בנקודה זו.

תיאור אינטואיטיבי

המחשה למושג המעגל הנושק מתוארת בפסקה הבאה. נניח כי מכונית נעה לאורך מסלול עקום כלשהו על פני כביש מישורי נרחב. כעת נניח כי ברגע מסוים במהלך תנועתה ובנקודה מסוימת על פני העקום ההגה שלה ננעל במצבו הנוכחי הרגעי. המעגל שהמכונית תתווה לאחר מכן כתוצאה מכך הוא המעגל הנושק לעקום בנקודה זו. רדיוסו הוא רדיוס העקמומיות של העקום בנקודת הנעילה ועקמומיותו היא כשל העקום בנקודת הנעילה.

תיאור מתמטי

יהי $\gamma (s)$ עקום פרמטרי רגולרי, כאשר $s$ הוא אורך הקשת של העקום ופרמטר לתיאורו. הצגה זו קובעת את וקטור היחידה המשיק $T$ , את וקטור היחידה הנורמלי, את העקמומיות $k(s)$ ואת רדיוס העקמומיות בכל נקודה על העקום:

$$T(s)=\gamma '(s)\ ,\ T'(s)=k(s)N(s)\ ,\ R(s)={\frac {1}{|k(s)|}}$$

נניח כי $P$ נקודה על העקום $C$ בה העקמומיות שונה מאפס. מרכז העקמומיות המתאים הוא בנקודה $Q$ במרחק $R$ לאורך $N$ , באותו הכיוון אם $k$ חיובי ובכיוון ההפוך אם $k$ שלילי. המעגל בעל המרכז $Q$ והרדיוס $R$ נקרא המעגל הנושק לעקום $C$ בנקודה $P$ .

אם $C$ הוא עקום מרחבי רגולרי אז המעגל הנושק מוגדר בצורה דומה, באמצעות וקטור הנורמל $N$ . המעגל שוכן במישור הנושק, המישור הנפרש על ידי הווקטור המשיק ווקטור הנורמל $T$ ו-$N$ בנקודה $P$ .

אם העקום המישורי נתון בפרמטריטזיציה רגולרית אחרת

$$\gamma (t)={\binom {x_{1}(t)}{x_{2}(t)}}$$

כאשר רגולרי פירושו $\gamma '(t)\neq 0$ לכל $t$ . אז הנוסחאות לעקמומיות $k(t)$ , וקטור היחידה הנורמלי $N(t)$ , רדיוס העקמומיות $R(t)$ והמרכז $Q(t)$ הן:

$${\begin{matrix}k(t)={\dfrac {x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}{\sqrt {{\bigl (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\bigr )}^{3}}}}\qquad N(t)={\dfrac {1}{\|\gamma '(t)\|}}\cdot {\dbinom {-x_{2}'(t)}{x_{1}'(t)}}\\\\R(t)=\left|{\dfrac {\sqrt {{\bigl (}x_{1}'(t)^{2}+x_{2}'(t)^{2}{\bigr )}^{3}}}{x_{1}'(t)\cdot x_{2}''(t)-x_{1}''(t)\cdot x_{2}'(t)}}\right|\qquad Q(t)=\gamma (t)+{\dfrac {1}{k(t)\cdot \|\gamma '(t)\|}}\cdot {\dbinom {-x_{2}'(t)}{x_{1}'(t)}}\end{matrix}}$$

תכונות

עבור עקום $C$ הנתון על ידי משוואות פרמטריות חלקות מספיק (גזירות ברציפות לפחות פעמיים), המעגל הנושק ניתן לבנייה באמצעות גבול מתאים:

גבול כל המעגלים העוברים דרך שלוש נקודות שונות על $C$ כאשר נקודות אלו שואפות ל-$P$ .

זה אנלוגי לחלוטין לבניית משיק לעקום כגבול של מיתרים העוברים דרך זוגות נקודות על $C$ כשאלו שואפות ל-$P$ .

המעגל הנושק $S$ לעקום מישורי $C$ בנקודה נתונה $P$ ניתן לאפיון באמצעות התכונות הבאות:

• המעגל $S$ חולף דרך $P$ .
• למעגל $S$ ולעקום $C$ יש משיק משותף בנקודה $P$ , ולפיכך גם קו נורמל משותף.
• בסביבת $P$ , המרחק בין הנקודות של העקום $C$ והמעגל $S$ בכיוון הנורמלי דועך לפי החזקה השלישית או חזקה גבוהה יותר של המרחק ל-$P$ בכיוון המשיקי.

באופן מילולי ניתן לומר כי "לעקום ולמעגל הנושק שלו יש מגע מסדר שני או גבוה יותר" ב-$P$ . במילים אחרות, הפונקציות הווקטוריות המייצגות את $C$ ואת $S$ זהות בנגזרות הראשונה והשנייה שלהן ב-$P$ .

אם הנגזרת של העקמומיות לפי $s$ שונה מאפס ב-$P$ אז המעגל הנושק בנקודה חוצה את העקום $C$ בנקודה $P$ . נקודות שבהן הנגזרת של העקמומיות היא אפס מכונות קודקוד של העקום. אם $P$ היא קודקוד אז לעקום $C$ ולמעגל הנושק לו בנקודה זו מגע מסדר רביעי לפחות. אם, יותר מכך, לעקמומיות יש אף מינימום או מקסימום מקומי שונה מאפס ב-$P$ , אזי המעגל הנושק נוגע בעקום $C$ ב-$P$ אבל אינו חוצה אותו.

העקום $C$ ניתן לבנייה כמעטפת של משפחה בת פרמטר אחד של המעגלים הנושקים שלו. מרכזיהם, דהיינו מרכזי העקמומיות שלהם, יוצרים עקום אחר, הנקרא האוולוט של $C$ . קודקודים על $C$ מתאימים לנקודות יחידות על האוולוט שלו.

דוגמאות

פרבולה

למעגל הנושק של הפרבולה בקודקוד שלה יש רדיוס 0.5 ומגע מסדר רביעי עמה

עבור הפרבולה

$\gamma (t)={\binom {t}{t^{2}}}$

ורדיוס העקמומיות הוא

$R(t)=\left|{\frac {\sqrt {(1+4t^{2})^{3}}}{2}}\right|$

בקודקוד מתקיים $\gamma (0)={\binom {0}{0}}$ ורדיוס העקמומיות שווה ל-0.5. לפרבולה יש מגע מסדר רביעי עם המעגל הנושק לה בנקודה זו. עבור $t$-ים גדולים רדיוס העקמומיות גדל בקצב יחסי ל-$t^{3}$ , והעקום הולך ונעשה קרוב יותר ויותר לישר.

עקום ליסאז'ו

תיאור המעגל הנושק לעקום ליסאז'ו

עקום ליסאז'ו בעל יחס תדירויות 2:3 ניתן להצגה פרמטרית באופן הבא:

$$\gamma (t)={\binom {\cos(3t)}{\sin(2t)}}$$

העקמומיות $k(t)$ , וקטור היחידה הנורמלי $N(t)$ ורדיוס העקמומיות $R(t)$ שלו הם:

$${\begin{matrix}k(t)={\dfrac {6\cos(t){\bigl (}8\cos(t)^{4}-10\cos(t)^{2}+5{\bigr )}}{\sqrt {{\bigl (}232\cos(t)^{4}-97\cos(t)^{2}-144\cos(t)^{6}+13{\bigr )}^{3}}}}\\\\N(t)={\dfrac {1}{\|\gamma '(t)\|}}\cdot {\dbinom {-2\cos(2t)}{-3\sin(3t)}}\\\\R(t)=\left|{\dfrac {\sqrt {{\bigl (}232\cos(t)^{4}-97\cos(t)^{2}-144\cos(t)^{6}+13{\bigr )}^{3}}}{6\cos(t){\bigl (}8\cos(t)^{4}-10\cos(t)^{2}+5{\bigr )}}}\right|\end{matrix}}$$

היסטוריה

פרק זה לוקה בחסר. אנא תרמו למכלול והשלימו אותו.

המעגל הנושק כונה כך על ידי לייבניץ. בנייה גאומטרית של המעגל תוארה על ידי אייזק ניוטון בספרו פרינקיפיה:

בהינתן, בכל מקום כלשהו, המהירות שבה גוף נתון מתווה צורה מסוימת, ובמונחים של כוח שכיוונו למרכז מסוים: למצוא את המרכז הזה

— אייזק ניוטון, פרינקיפיה, טענה 5, בעיה 1.

ראו גם

• רדיוס עקמומיות
• עקמומיות
• מישור נושק

לקריאה נוספת

• מבוא לגאומטריה דיפרנציאלית, מיכאל פרבר

קישורים חיצוניים

מדיה וקבצים בנושא מעגל נושק בוויקישיתוף