מרחב פרויקטיבי ממשי

בטופולוגיה, מרחב פרויקטיבי ממשי (Real projective space) הוא מרחב פרויקטיבי מעל שדה המספרים הממשיים. המרחב הפרויקטיבי $\mathbb {R} P^{n}$ הוא משטח קומפקטי חלק $n$-ממדי, והוא אוריינטבילי אם ורק אם הסדר שלו אי-זוגי.

הקדמה

במקרה החד-ממדי, המרחב מכונה ישר פרויקטיבי ממשי. מבחינה אינטואיטיבית נתן להתייחס אליו כישר בגאומטריה הרגילה, בתוספת נקודה מיוחדת, הנקראת הנקודה באינסוף, שאינה שוכנת על הישר, אלא כביכול בשני קצותיו ($\infty$ או $-\infty$). הנקודה באינסוף מעניקה לכל ישר פרויקטיבי מבנה של מעגל: ישר כזה כולל את הישר המתאים מן המישור הרגיל, בתוספת נקודת האינסוף, שאינה שוכנת על הישר. בניגוד לגישה באנליזה, ונקודת האינסוף ממלאת את שני התפקידים בו-זמנית.

במקרה הדו-ממדי, אנו עוסקים במישור פרויקטיבי ממשי, הבנוי מאוסף אינסופי של ישרים פרויקטיביים (בהקבלה למישור הממשי הרגיל הבנוי מאוסף של ישרים). כל ישר פרויקטיבי, כאמור, מורכב מישר רגיל ונקודת אינסוף. אולם, במישור הפרויקטיבי הממשי, נקודת האינסוף של כל קבוצת ישרים מקבילים היא משותפת. כך, לכל כיוון ישנה נקודת אינסוף, בה נפגשים כל הישרים שהם בעלי שיפוע מסוים. כלומר, בהינתן $a\in \mathbb {R}$ כלשהו, קבוצת כל הישרים שמשוואתם היא ${\bigl \{}y=ax+b:b\in \mathbb {R} {\bigr \}}$ , מגדירה נקודת אינסוף בכיוון זה. באופן זה נקבל שכל שני ישרים במישור הפרויקטיבי נפגשים: ישרים בעלי שיפוע שונה נפגשים בנקודה סופית, רגילה, וישרים בעלי אותו שיפוע נפגשים בנקודה אינסופית. על מנת להשלים את הבניה, ובכדי שבין כל זוג נקודות יעבור ישר, נוסיף את "ישר האינסוף", שהוא ישר מיוחד המורכב מאוסף כל נקודות האינסוף.

הגדרה

המרחב הפרויקטיבי מעל שדה הממשיים

הרחב הפרויקטיבי הממשי הוא אוסף מחלקות השקילות של הקבוצה $\mathbb {R} ^{n+1}\setminus \{0\}$ תחת זיהוי ישרים – $x\sim \lambda x$ לכל $\lambda \neq 0$ . מתקבל מרחב, שניתן להגדיר עליו מבנה של מרחב טופולוגי, בעזרת טופולוגיית המנה.

טופולוגית

לפי היחס שהוגדר לעיל, למעשה מספיק לדבר על וקטורים מנורמה 1, היינו איברים של הספירה. היחס הנורש על $S^{n}$ הוא זיהוי נקודות אנטיפודיות, ולכן המרחב הפרויקטיבי למעשה שווה ל-$S^{n}/v\sim -v$ .

ניתן להמשיך ולהקטין את המרחב עליו עושים את המנה; המרחב המינימלי שאפשר לקחת הוא ההמיספירה העליונה $S_{+}^{n}=\{{\bar {x}}\in S^{n}:x_{n}\geq 0\}$ (כולל השפה התחתונה). לכן, המרחב הפרויקטיבי שקול לדיסק $n$-ממדי בו מזהים נקודות אנטיפודיות על השפה $x_{n}=0$ .

מרחב המסלולים של ספירה

ההעתקה האנטיפודית מגדירה $\mathbb {Z} /2\mathbb {Z}$-פעולה על הספירה $S^{n}$ , ו-$\mathbb {R} P^{n}$ הוא מרחב המסלולים שלה. תחת העתקה המנה, $S^{n}$ מהווה מרחב כיסוי מסדר 2 של המרחב הפרויקטיבי.

סימונים מתחומים שונים

למרחב הפרויקטיבי מספר סימונים המגיעים מתחומים שונים.

בהתאם לסימון הסטנדרטי של מרחבים פרויקטיביים, הוא מסומן ${\mathbb {P}}(\mathbb {R} ^{n})$ . למרות זאת, בהקשר הטופולוגי הוא קיבל את הסימון מיוחד $\mathbb {R} P^{n}$ ; נראה כי זהו הסימון הנפוץ ביותר. בגאומטריה אלגברית הסימן המקובל הוא ${\mathbb {P}}_{\mathbb {R} }^{n}$ .

מרחבים פרויקטיבים מממדים נמוכים

הישר הפרויקטיבי

איור 1

הטלה מרכזית (perspective projection, הטלה פרספקטיבית) היא העתקה המעבירה נקודה אחת לנקודה שנייה ביחס לנקודת מוקד. על מנת לבצע הטלה מרכזית יש לבחור נקודת מוקד וטווח אליו תועתקנה הנקודות. בהינתן נקודה $x$ במרחב, נבחר את הישר המחבר אותה לנקודת המוקד (ישנו ישר יחיד כזה) ונחתוך אותו עם הטווח שלנו. נקודת החיתוך, אם ישנה כזו, היא התמונה של $x$ . בהנחות היסוד לגבי ציור בפרספקטיבה, הציור הוא הטלה פרספקטיבית של העצם המצויר. עינו של הצייר היא מוקד ההטלה ובד הציור הוא הטווח אליו מוטל מושא הציור. מסיבה זו, נהוג להתייחס לישרים העוברים בנקודת המוקד כ"כיוונים" אליהם מסתכלת נקודת המוקד.

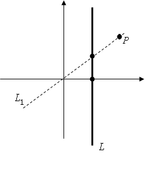
הישר הפרויקטיבי (פרויקציה = הטלה) זכה בשמו בשל ההתאמה בין הנקודות שעליו, לכיוון ממנו רואים אותן מנקודה קבועה. לשם הפשטות, נגדיר נקודת מוקד בראשית הצירים $(0,0)$ ונגדיר את הישר $L={\bigl \{}(1,y):y\in \mathbb {R} {\bigr \}}$ להיות טווח ההטלה. נטיל את הנקודה $P=(3,3)$ אל $L$ ביחס לראשית הצירים. לשם כך, עלינו לחבר את הנקודה $P$ עם ראשית הצירים, על ידי הישר (הכיוון) $L_{1}$ . נקודת החיתוך של $L_{1}$ עם $L$ היא בנקודה $(1,1)$ , וזוהי תוצאת ההטלה. באופן זה ניתן להטיל כל נקודה ${\bigl \{}(x,y):x\neq 0{\bigr \}}$ במישור הממשי אל הטווח $L$ , והיא תוטל ל-$\left(1,{\tfrac {y}{x}}\right)$ . את הנקודות שבכיוון הציר האנכי לא נוכל להטיל אל הטווח $L$ . לשם כך אנו מוסיפים לטווח את נקודת האינסוף, המייצגת הסתכלות מנקודת המוקד בכיוון המקביל לישר $L$ . כך קבלנו התאמה בין ישר פרויקטיבי ובין אוסף כל כיווני המבט מנקודה קבועה.

טופולוגית, לפי הזיהוי האחרון לעיל, בישר הפרויקטיבי מזהים בחצי המעגל את שתי נקודות הקצה, ולכן הוא בעצמו שקול למעגל.

מישור פרויקטיבי

המקרה המעניין הראשון והחשוב הוא המישור הפרויקטיבי $P=\mathbb {R} P^{2}$ .

איור 2

המרחב הפרויקטיבי ${\mathbb {PR}}^{2}$ מוגדר באופן דומה. נגדיר שוב את ראשית הצירים של המרחב האוקלידי התלת-ממדי כמוקד ההטלה, ונגדיר את העל-מישור $H:={\bigl \{}(x,y,1):x,y\in \mathbb {R} {\bigr \}}$ כטווח ההטלה. שוב, כל נקודה $\{(x,y,z):z\neq 0\}$ תוטל אל $\left({\tfrac {x}{z}},{\tfrac {y}{z}},1\right)\in H$ . כך, כל כיוון שאליו מביטים מראשית הצירים יחתך עם $H$ , להוציא המישור $I:={\bigl \{}(x,y,0):x,y\in \mathbb {R} {\bigr \}}$ . לכן כל כיוון $L_{a}:={\bigl \{}(x,ax,0):x\in \mathbb {R} {\bigr \}}$ המוכל במישור $I$ יגדיר נקודות אינסוף במישור הפרויקטיבי.

פרט להגדרות לעיל, יש לו אפיון נוסף כסכום קשיר של טבעת מביוס עם מעגל. הבחנה זו עוזרת לחשב את החבורה היסודית שלו, בעזרת משפט ואן קמפן.

מבנה כמשטח

כל מרחב פרויקטיבי הוא משטח קומפקטי חלק. אחת הדרכים לתת את הכיסוי על ידי סביבות שהומיאומורפיות למרחב ממשי הוא בעזרת כיסוי גאומטרי של המרחב על ידי $n+1$ סביבות: $\mathbb {R} P^{n}=\cup _{i=1}^{n+1}{\mathbb {A} _{\mathbb {R} _{i}}^{n}}$, כאשר $\mathbb {A} _{\mathbb {R} _{i}}=\{{\bar {x}}\in \mathbb {R} P^{n}:x_{i}\neq 0\}$ - סביבה אפינית. מבנה זה אכן מגדיר מבנה של משטח, לפי ההעתקות $\mathbb {A} _{\mathbb {R} _{i}}\to \mathbb {R} ^{n}$ הנתונות על ידי $(x_{1}:\dots :x_{n+1})\to \left({\frac {x_{1}}{x_{i}}},\dots ,{\frac {x_{n+1}}{x_{i}}}\right)$. העתקות אלו חלקות, ולכן המבנה שהוגדר הוא משטח חלק.

מבנה CW

בעזרת התיאור הטופולוגי לעיל, ניתן לתת מבנה של מרחב CW ל-$\mathbb {R} P^{n}$. ניעזר בשני הפירושים הטופולוגיים - ראשית, $\mathbb {R} P^{n}$ הוא דיסק $n$-ממדי תחת זיהוי נקודות אנטיפודיות על שפת ההימספירה - שהיא $S^{n-1}$, וזיהוי זה בדיוק מגדיר את $\mathbb {R} P^{n-1}$. לכן מתקיים $\mathbb {R} P^{n}=D^{n}\cup _{f}\mathbb {R} P^{n-1}$, כאשר $f$ היא ההדבקה שמגדירה את $\mathbb {R} P^{n-1}$.

לכן, בכל ממד יש תא אחד: $1=d_{0}=d_{1}=\dots =d_{n}$, וההדבקות בכל שלב הן בדיוק ההדבקות מהבנייה.

אינווריאנטים טופולוגיים

החבורה היסודית

כאמור לעיל, $S^{n}$ מהווה מרחב כיסוי מסדר 2 של $\mathbb {R} P^{n}$. היות ש-$S^{n}$ פשוט קשר לכל $n\geq 2$, הוא מהווה מרחב כיסוי אוניברסלי של המרחב הפרויקטיבי. לכן, $\pi _{1}(\mathbb {R} P^{n})=\mathbb {Z} /2\mathbb {Z}$ לכל $n>1$. יוצר לחבורה הוא התמונה של העתקה המהווה חצי סיבוב על הספירה בין שתי נקודות אנטיפודיות.

משיקולים אלו ניתן להוכיח שמרחב פרויקטיבי הוא אוריינטבילי אם ורק אם ממדו אי-זוגי - קרקטר האוריינטציות שלו פועל על הלולאה הסגורה כלעיל כ-$(-1)^{n+1}$, ולכן הוא טריוויאלי אם ורק אם $n$ אי-זוגי.

חבורות ההומוטופיה

ביתר כלליות, בעזרת הסדרה המדויקת הארוכה של חבורות ההומוטופיה היחסיות המפועלת על הכיסוי $\mathbb {Z} /2\mathbb {Z} \to S^{n}\to \mathbb {R} P^{n}$, ניתן לחשב את כל חבורות ההומוטופיה של המרחב:

$\pi _{i}(\mathbb {R} P^{n})={\begin{cases}0&i=0\\\mathbb {Z} &i=1,n=1\\\mathbb {Z} /2\mathbb {Z} &i=1,n>1\\\pi _{i}(S^{n})&i>1,n>0.\end{cases}}$

חבורות ההומולוגיה

בעזרת מבנה ה-CW כלעיל ובעזרת האלגוריתם לחישוב חבורות ההומולוגיה, ניתן לחשב את כל חבורות ההומולוגיה של $\mathbb {R} P^{n}$ - הן שוות

$H_{i}(\mathbb {R} P^{n})={\begin{cases}\mathbb {Z} &i=0{\mbox{ or }}i=n{\mbox{ odd,}}\\\mathbb {Z} /2\mathbb {Z} &0<i<n,\ i\ {\mbox{odd,}}\\0&{\mbox{else.}}\end{cases}}$

n-מישור פרויקטיבי

n-מישור פרויקטיבי הוא סכום קשיר של $n$ מישורים פרויקטיביים, מסומן $nP$. זהו משטח סגור, ויחד עם הספירות והטורוסים הוא משלים את אוסף כל המשטחים הסגורים.

למרחב זה חבורה יסודית $\langle x_{1},\dots ,x_{n}\mid x_{1}^{2}\cdots x_{n}^{2}=1\rangle$ (ראו משפט ואן קמפן לפרטים); האבליניזציה שלה $\mathbb {Z} /2\mathbb {Z} \times \mathbb {Z} ^{n-1}$ היא חבורת ההומולוגיה הראשונה שלו, והיחידה שאיננה אפס.

מרחב זה איננו אוריינטיבילי אף פעם. באופן כללי, אף מחובר בסכום קשיר עם מרחב לא אוריינטיבילי (ובפרט, עם $P$) איננו אוריינטבילי.

מרחב פרויקטיבי ממשי אינסוף-ממדי

המרחב הפרויקטיבי האינסופי $\mathbb {R} P^{\infty }$ הוא הגבול הישר של המרחבים הפרויקטיביים הממשיים הסוף-ממדיים. באופן זה מושרית עליו טופולוגיה, כגבול של מרחבים טופולוגיים. בדומה למקרה הסופי, הספירה האינסוף-ממדית $S^{\infty }$ מהווה כיסוי מסדר 2 למרחב. היות שהיא כוייצה, היא מהווה כיסוי אוניברסלי. כן, $\mathbb {R} P^{\infty }$ הוא בעל חבורת הומוטופיה לא טריוויאלית אחת בלבד, כלומר הוא מרחב אילנברג-מקליין $K(\mathbb {Z} /2\mathbb {Z} ,1)$.

ראו גם

• מרחב פרויקטיבי
• מרחב פרויקטיבי מרוכב
• מרחב פרויקטיבי קווטרניוני