משוואת בורדה-קרנו

במכניקת הזורמים, משוואת בורדה-קרנו מספקת תיאור חצי-אמפירי של אובדן האנרגיה המכנית של זורם אודות להתרחבות פתאומית של שפופרת הזרימה. היא מתארת כיצד העומד ההידראולי הכולל פוחת עקב ההפסדים. משוואה זו מתארת מצב שונה ממשוואת ברנולי, אשר מתייחסת לזרימה ללא שחיקה אנרגטית (ללא תהליכים בלתי-הפיכים) - מצב שבו העומד הכולל קבוע לאורך קו זרם. המשוואה נקראת על שם Jean-Charles de Borda (חי בשנים 1799–1733) ולזאר קרנו (1823 - 1753).

במשוואה נעשה שימוש הן במקרה של זרימה בתעלה והן במקרה של זרימה בצנרת. בחלקים של הזרימה בהם אובדן האנרגיה זניח, ניתן לעשות שימוש בעקרון ברנולי.

ניסוח

משוואת בורדה-קרנו היא:

$\Delta E\,=\,\xi \,{\scriptstyle {\frac {1}{2}}}\,\rho \,\left(v_{1}\,-\,v_{2}\right)^{2},$

כאשר

• ΔE הוא אובדן האנרגיה המכנית של הזורם,
• ξ הוא מקדם אמפירי, שהינו גודל חסר ממד שמקבל ערכים בין 0 ל-1,
• ρ היא צפיפות הזורם
• v₁ ו-v₂ הן מהירויות הזרימה הממוצעות לפני ואחרי ההתרחבות.

במקרה של התרחבות ניכרת ופתאומית מקדם האובדן שווה לאחד. במקרים אחרים, מקדם האובדן צריך להיקבע בדרכים אחרות, לעיתים קרובות דרך נוסחאות אמפיריות (הנגזרות ממידע המושג דרך ניסויים). משוואת בורדה-קרנו תקפה רק עבור מהירויות יורדות, כלומר כאשר v₁ > v₂, אחרת אובדן האנרגיה ΔE הוא אפס.

מקדם האובדן ξ מושפע רבות ממיטוב הזרימה. לדוגמה, במקרה של זרימה בצנרת, תכנון הצנרת כך שתביא להתרחבות הדרגתית של הזרימה יכולה להפחית רבות את אובדן האנרגיה המכנית.

קשר המשוואה לעומד הכולל ולעקרון ברנולי

משוואת בורדה-קרנו מאפשרת לחשב כיצד פוחת הקבוע של משוואת ברנולי. בעבור זרימה אי-דחיסה התוצאה היא - בעבור שתי מיקומים שנסמנם 1 ו-2, כשמיקום 2 נמצא במורד הזרם ביחס לנקודה 1 - שלאורך קו זרם מתקיים:

$p_{1}\,+\,{\scriptstyle {\frac {1}{2}}}\,\rho \,v_{1}^{2}\,+\,\rho \,g\,z_{1}\,=\,p_{2}\,+\,{\scriptstyle {\frac {1}{2}}}\,\rho \,v_{2}^{2}\,+\,\rho \,g\,z_{2}\,+\,\Delta E,$

כאשר

• p₁ ו-p₂ הם הלחצים בנקודות 1 ו-2,
• z₁ ו-z₂ הם הגבהים - ביחס לגובה ייחוס מסוים - של אלמנט הזורם,
• g היא תאוצת הכובד

שלושת האיברים הראשונים בכל אחד מהצדדים של סימן השוויון הם בהתאמה הלחץ, צפיפות האנרגיה הקינטית וצפיפות האנרגיה הפוטנציאלית אודות לכבידה. כפי שניתן לראות, הלחץ פועל כצורה של אנרגיה פוטנציאלית.

במקרים של זרימה בלחץ גבוה בצנרת, כאשר אפקטים כבידתיים (שינוי גובה) ניתנים להזנחה, ΔE שווה לאובדן (Δ(p+½ρv²:

$\Delta E\,=\,\Delta \left(p\,+\,{\scriptstyle {\frac {1}{2}}}\,\rho \,v^{2}\right).$

בעבור זרימה בתעלה, ΔE קשור באובדן העומד הכולל ΔH באופן הבא:

$\Delta E\,=\,\rho \,g\,\Delta H,$ כאשר H הוא העומד הכולל : $H\,=\,h\,+\,{\frac {v^{2}}{2g}},$

כאשר h הוא העומד ההידראולי.

דוגמאות

התרחבות פתאומית של צינור

התרחבות זרימה פתאומית.

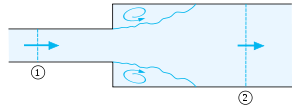
ניישם את משוואת בורדה-קרנו לזרימה דרך צינור אופקי שמתרחב באופן פתאומי. בחתך 1, מהירות הזרימה הממוצעת שווה ל-v₁, הלחץ הוא p₁ ושטח החתך הוא A₁. גדלי הזרימה המתאימים בחתך 2 - הרבה מאחורי אזור ההתרחבות - הם v₂, p₂ ו-A₂, בהתאמה. באזור ההתרחבות, הזורם לא מצליח לעקוב אחרי הדופן ונוצרים אזורי סירקולציה טורבולנטיים בסמוך לפינות - מערבולות קטנות שמכלות חלק מהאנרגיה של הזרימה וגורמות לאובדן לחץ. מקדם האובדן ξ בעבור ההתרחבות הפתאומית הזאת שווה בקירוב לאחד: ξ ≈ 1.0. אודות לשימור המסה, תחת ההנחה של צפיפות זורם קבועה ρ, הספיקה הנפחית דרך חתכים 1 ו-2 חייבת להיות שווה:

$A_{1}\,v_{1}\,=A_{2}\,v_{2}$     כך ש-     $v_{2}\,=\,{\frac {A_{1}}{A_{2}}}\,v_{1}$.

כתוצאה מכך - לפי משוואת בורדה-קרנו - אובדן האנרגיה המכנית בהתרחבות הפתאומית הזאת הוא:

$\Delta E\,=\,{\frac {1}{2}}\,\rho \,\left(1\,-\,{\frac {A_{1}}{A_{2}}}\right)^{2}\,v_{1}^{2}.$

אובדן העומד הכולל המתאים הוא:

$\Delta H\,=\,{\frac {\Delta E}{\rho \,g}}\,=\,{\frac {1}{2\,g}}\,\left(1\,-\,{\frac {A_{1}}{A_{2}}}\right)^{2}\,v_{1}^{2}.$

במקרה זה ξ = 1, והשינוי הכולל באנרגיה הקינטית בין שני חתכים נשחק. כתוצאה, שינוי הלחץ בין שני החתכים הוא (בעבור צינור אופקי):

$\Delta p\,=\,p_{1}\,-\,p_{2}\,=\,-\,\rho \,{\frac {A_{1}}{A_{2}}}\left(1\,-\,{\frac {A_{1}}{A_{2}}}\right)\,v_{1}^{2},$

והשינוי בעומד ההידראולי (h = z + p/(ρg:

$\Delta h\,=\,h_{1}\,-\,h_{2}\,=\,-\,{\frac {1}{g}}\,{\frac {A_{1}}{A_{2}}}\left(1\,-\,{\frac {A_{1}}{A_{2}}}\right)\,v_{1}^{2}.$

סימן המינוס הזה באגף ימין פירושו שהלחץ (והעומד ההידראולי) גדולים יותר אחרי התרחבות הצינור. העובדה שהשינוי הזה בלחצים (מיד לפני ואחרי התרחבות הצינור) משקף אובדן אנרגיה נעשית ברורה כאשר משווים את השינוי עם זה שמנבאת משוואת ברנולי - לפי עקרון זה, הירידה במהירות הזורם מקושרת לעלייה גבוהה בהרבה בלחץ מאשר זה שבמקרה הזה (שבו יש אובדן מכנית).

היצרות פתאומית של צינור

זרימה דרך היצרות פתאומית בקוטר הצינור.

במקרה של היצרות פתאומית בקוטר הצינור, הזורם אינו מסוגל לעקוב אחרי הדופן, ולכן מגיע לחלק הצר יותר של הצינור כשמהירותו לא לגמרי אופקית. כתוצאה, שכבת הזורם שצמודה לדופן מתנתקת ממנה, מה שיוצר אזורי סירקולציה בכניסה לחלק הצינור הצר יותר. שפופרת הזרימה עוברת היצרות באזור הכניסה לחלק הצינור הצר, ולאחר מכן מתרחבת שוב ומכסה את מלוא שטח הצינור (ראו איור משמאל).

אין הרבה אובדן עומד בין חתך 1, לפני ההיצרות, לחתך 3, הונה קונטרקטה שבה הזרימה הראשית מוצרת במידה מרבית. אבל יש הפסדים משמעותיים בהתרחבות הזרימה מחתך 3 לחתך 2. הפסדי העומד הללו ניתנים לחישוב דרך משוואת בורדה-קרנו, זאת באמצעות שימוש במקדם ההיצרות μ:

$\mu \,=\,{\frac {A_{3}}{A_{2}}},$

כאשר A₃ שטח החתך באזור ההיצרות המרבית של הזרימה הראשית (חתך 3), ו-A₂ שטח החתך של חלקו הצר של הצינור. מכיוון ש-A₃ ≤ A₂, מקדם ההיצרות קטן מאחד: μ ≤ 1. כמו במקרה הקודם שטופל ישנו שימור מסה, כך שהספיקה הנפחית בשלושת החתכים קבועה (בעבור צפיפות זורם קבועה ρ):

$A_{1}\,v_{1}\,=\,A_{2}\,v_{2}\,=\,A_{3}\,v_{3},$

כאשר v₁, v₂ ו-v₃ הן מהירויות הזרימה הממוצעות בחתכים המתאימים. לפיכך, בהתאם למשוואת בורדה-קרנו (עם מקדם אובדן ξ=1), אובדן האנרגיה ליחידת נפח זורם ΔE הוא:

$\Delta E\,=\,{\frac {1}{2}}\,\rho \,\left(v_{3}\,-\,v_{2}\right)^{2}\,=\,{\frac {1}{2}}\,\rho \,\left({\frac {1}{\mu }}\,-\,1\right)^{2}\,v_{2}^{2}\,=\,{\frac {1}{2}}\,\rho \,\left({\frac {1}{\mu }}\,-\,1\right)^{2}\,\left({\frac {A_{1}}{A_{2}}}\right)^{2}\,v_{1}^{2}.$

אובדן העומד הכולל המתאים ΔH ניתן לחישוב באמצעות הקשר (ΔH = ΔE/(ρg.

לפי מדידות של יוליוס וייסבאך (Julius Weisbach), מקדם ההיצרות בעבור היצרות בסמוך לפינה חדה הוא בקירוב  :

$\mu \,=\,0.63\,+\,0.37\,\left({\frac {A_{2}}{A_{1}}}\right)^{3}$.

גזירת המשוואה ממשוואת שימור התנע בעבור התרחבות פתאומית

בעבור התרחבות פתאומית בצינור, משוואת בורדה-קרנו ניתנת לגזירה משימור המסה והתנע של הזרימה. שטף התנע S (של רכיב התנע של הזורם המקביל לציר הצינור) דרך חתך בשטח A הינו - לפי משוואות אוילר:

$S=A\,\left(\rho \,v^{2}+p\right)$.

נתייחס לשימור המסה והתנע עבור נפח בקרה התחום על ידי חתך 1 ממש לפני ההתרחבות, חתך 2 במורד הזרם שבו הזורם נצמד מחדש לדופן הצינור (אחרי ההפרדה שלו באזור ההתרחבות), ודופן הצינור. נפח הבקרה קולט תנע בסך S₁ עקב הזרם הנכנס אליו ומאבד תנע בסך S₂ עקב הזרם היוצא ממנו. חוץ מכך, ישנה גם התרומה של הכוח F הנגרם מלחץ התגובה שמפעילה דופן ההתרחבות על הזורם (מדובר על חלק הצינור הניצב לצירו):

$F=(A_{2}-A_{1})\,p_{1},$

כשמסכמים את התרומות, משוואת מאזן התנע בעבור נפח הבקרה בין החתכים 1 ו-2 נותנת:

$S_{1}-S_{2}+F=A_{1}\,\left(\rho \,v_{1}^{2}+p_{1}\right)-A_{2}\,\left(\rho \,v_{2}^{2}+p_{2}\right)+(A_{2}-A_{1})\,p_{1}=0$.

מכיוון שעקב שימור המסה מתקיים ρ A₁ v₁ = ρ A₂ v₂, נקבל:

$\Delta p=p_{1}-p_{2}=-\rho \,\left({\frac {A_{1}}{A_{2}}}\,v_{1}^{2}-v_{2}^{2}\right)=-\rho \,{\frac {A_{1}}{A_{2}}}\,\left(1-{\frac {A_{1}}{A_{2}}}\right)\,v_{1}^{2},$

בהתאמה עם נפילת הלחץ Δp בדוגמה לעיל. אובדן האנרגיה המכנית ΔE הוא:

${\begin{aligned}\Delta E&=\left(p_{1}+{\tfrac {1}{2}}\,\rho \,v_{1}^{2}\right)-\left(p_{2}+{\tfrac {1}{2}}\,\rho \,v_{2}^{2}\right)=\Delta p+{\tfrac {1}{2}}\,\rho \,\left(v_{1}^{2}-v_{2}^{2}\right)\\&=-\rho \,v_{2}\,\left(v_{1}-v_{2}\right)+{\tfrac {1}{2}}\,\rho \,\left(v_{1}^{2}-v_{2}^{2}\right)={\tfrac {1}{2}}\,\rho \,\left(v_{1}^{2}-2\,v_{1}\,v_{2}+v_{2}^{2}\right)\\&={\tfrac {1}{2}}\,\rho \,\left(v_{1}-v_{2}\right)^{2},\end{aligned}}$

תוצאה זאת היא משוואת בורדה-קרנו (עם ξ = 1).

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

23455366משוואת בורדה-קרנו