פונקציות היפרבוליות
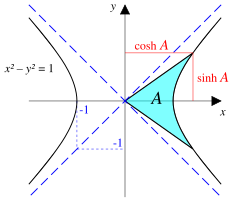
במתמטיקה, פונקציות היפרבוליות אנלוגיות לפונקציות הטריגונומטריות הרגילות: בעוד שהנקודות יוצרות יחדיו מעגל, הנקודות מגדירות את החלק הימני של ההיפרבולה , ומכאן שמן. הפרמטר הוא זווית היפרבולית המייצגת את כפליים השטח בין ציר ה־X, ההיפרבולה, והקו הישר שמחבר את ראשית הצירים לנקודה על העקום לעיל, כפי שמתואר באיור משמאל.
הגדרת הפונקציות ההיפרבוליות
גרפי הפונקציות ההיפרבוליות נראות כך:


בהינתן (ראו מספרים מרוכבים) הפונקציות ההיפרבוליות הן:
סינוס היפרבולי:
קוסינוס היפרבולי:
טנגנס היפרבולי:
קוטנגנס היפרבולי:
סקאנט היפרבולי:
קוסקאנט היפרבולי:
הגדרה לפי טורים
ניתן להביע את הפונקציות ההיפרבוליות כטורים:
כאשר:
- , הוא מספר ברנולי ה-n־י
- , הוא מספר אוילר ה-n־י.
קשרים לפונקציות טריגונומטריות

כשם שהנקודות מגדירות מעגל, הנקודות מגדירות את החלק הימני של ההיפרבולה (הקביעה מתבססת על הזהות ועל כך ש- לכל ). הפרמטר איננו זווית מעגלית, אלא זווית היפרבולית שמייצגת את פעמיים השטח בין ציר ה-x, ההיפרבולה, והקו הישר שמחבר את ראשית הצירים לנקודה על ההיפרבולה .
למרות זאת, הפונקציות ההיפרבוליות אינן פונקציות מחזוריות, בניגוד לפונקציות הטריגונומטריות הרגילות, שכן בהצגתן המעריכית של הפונקציות הטריגונומטריות הרגילות ישנו חלק מעריכי מרוכב אשר תורם למחזוריות הפונקציה, אך נעדר מן הפונקציות ההיפרבוליות.
ההצגות המעריכיות של הפונקציות ההיפרבוליות והרגילות הן דומות, פרט, כאמור, לקיומו של החלק המרוכב בפונקציות הטריגונומטריות הרגילות. כך, למשל, פונקציית הסינוס מוגדרת כך: בעוד מקבילתה ההיפרבולית מוגדרת כך, כאמור:
. בדומה לפונקציה , הפונקציה היא פונקציה זוגית (סימטרית סביב ציר Y)ו־cosh 0=1. באופן דומה, הן הפונקציה והן הפונקציה הן פונקציות אי זוגית (סימטרית סביב ראשית הצירים) ו . הפונקציות ההיפרבוליות מקיימות זהויות רבות, כולן דומות לזהויות טריגונומטריות. למעשה, חוק אוסבורן מראה שניתן להמיר כל זהות טריגונומטרית לזהות היפרבולית, על ידי החלפת סינוס בסינוס היפרבולי, קוסינוס בקוסינוס היפרבולי, והפיכת הסימן של כל מונום שיש בו מכפלה של שני סינוסים היפרבוליים. לדוגמה:
זהויות נוספות
הפונקציות ההפוכות לפונקציות ההיפרבוליות

 ערך מורחב – פונקציות היפרבוליות הפוכות
ערך מורחב – פונקציות היפרבוליות הפוכות
השמות של פונקציות אלו מתחילים בתחילית (קיצור של area/שטח) או .
הגדרת הפונקציות ההפוכות לפונקציות ההיפרבוליות כטורים
ניתן להביע את הפונקציות ההפוכות לפונקציות ההיפרבוליות כטורים:
פונקציות היפרבוליות עבור מספרים מרוכבים
פונקציות היפרבוליות יכולות לקבל בתור ארגומנט מספר מרוכב. ניתן, בעזרת נוסחת אוילר () להגיע לקשרים הבאים בין הפונקציות ההיפרבוליות לפונקציות הטריגונומטריות עבור ארגומנטים מרוכבים:
במשוואות הבאות, :
שימושים בפונקציות היפרבוליות
הפונקציות ההיפרבוליות מופיעות בבעיות רבות בתחומי המתמטיקה והפיזיקה, בהן מעורב אינטגרל המכיל את הביטוי : (זאת בעוד שהפונקציות הטריגונומטריות מופיעות בבעיות, בהן מעורב אינטגרל המכיל את הביטוי :).
דוגמות:
- קוסינוס היפרבולי הוא הפונקציה המתארת את צורתו של כבל תלוי בין שני עמודים (עקומת קו השרשרת).
- טנגנס היפרבולי הוא הפונקציה המתארת את מהירותו של עצם הנופל נפילה חופשית כשהוא נתון להשפעתם של כוח הכובד ושל כוח התנגדות האוויר.
- סינוס היפרבולי מופיע בביטוי לפוטנציאל הכבידתי של גליל, ובחישוב גבול רוש (Roche limit).
- טנגנס היפרבולי מופיע בחישובי מהירות בתורת היחסות הפרטית.
- סינוס, קוסינוס וטנגנס היפרבוליים מופיעים בחישובי תורת היחסות הכללית.
- הפונקציות ההיפרבוליות מופיעות במשפטים בגאומטריה היפרבולית.
- מבנה קשת השער מתוכנן על בסיס של פונקציית קוסינוס היפרבולי.
נגזרות של פונקציות היפרבוליות
ראו גם
קישורים חיצוניים
- פונקציות היפרבוליות, באתר MathWorld (באנגלית)
- פונקציות היפרבוליות, באתר אנציקלופדיה בריטניקה (באנגלית)
 פונקציות מעריכיות, דף שער בספרייה הלאומית
פונקציות מעריכיות, דף שער בספרייה הלאומית
פונקציות היפרבוליות38338832Q204034


