תכונת ארכימדס

במתמטיקה, תכונת ארכימדס היא תכונה של מבנה אלגברי סדור, כמו חבורה סדורה או שדה סדור: המבנה מקיים את תכונת ארכימדס אם קבוצת המספרים הטבעיים הנמצאת בו אינה חסומה: לכל איבר x יש מספר טבעי n הגדול ממנו. במילים אחרות, מספר השייך למבנה אינו יכול להיות גדול מכל המספרים הטבעיים - 'גדול עד אינסוף'; בדרך כלל נובע מכך גם שמספר חיובי השייך למבנה אינו יכול להיות 'קטן עד אינסוף'. שדה המקיים תכונה זו נקרא שדה ארכימדי. לדוגמה, השדה הרציונלי והשדה הממשי הם ארכימדיים, בעוד ששדה הפונקציות הרציונליות , הסדור כך ש-x נעשה אינפיניטסימל, אינו ארכימדי.
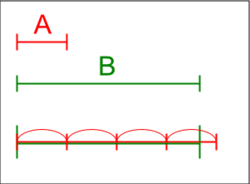
התכונה קרויה על שם ארכימדס מסירקוזה, שקבע בתור ההנחה החמישית בספרו על הכדור והגליל שניתן להשוות כל שני קטעים ממשיים: אם מניחים עותקים של הקטע הקצר בזה אחר זה, בסופו של דבר אפשר יהיה לעבור את הקטע הארוך.[1] התכונה מופיעה בספר הרביעי מספרי ה"יסודות" של אוקלידס. בניסוח מודרני, זוהי בדיוק תכונת הארכימדיות של השדה הממשי.
תכונת ארכימדס מופיעה בהקשר אחר, של הערכות מוחלטות, ושם יש לה מובן שונה (אם כי קרוב ברוחו למובן המוצג כאן).
ראו גם
קישורים חיצוניים
הערות שוליים
- ↑ ארכימדס, על הכדור והגליל, הנחה 5
תכונת ארכימדס38717405Q634579


