צימוד תרמי

מערכת בטמפרטורה התחלתית של 0° (בכחול) נמצאת בצימוד תרמי עם מערכת בטמפרטורה התחלתית של 100° (באדום). חום יזרום מהמערכת החמה לקרה עד אשר יתקיים שוויון טמפרטורות (למטה).

צימוד תרמי (באנגלית: Thermal contact) הוא מושג בתרמודינמיקה ופיזיקה תרמית המתאר אינטראקציה בין שתי מערכות תרמודינמיות (או יותר), בה מתאפשר חילוף אנרגיה תרמית בין המערכות על ידי הולכת חום.

כאשר שתי מערכות תרמודינמיות נמצאות בצימוד תרמי, חום יזרום מהמערכת בעלת הטמפרטורה הגבוהה יותר (המערכת החמה) למערכת בעלת הטמפרטורה הנמוכה יותר (המערכת הקרה). כתוצאה מכך תרד טמפרטורת המערכת החמה, המאבדת אנרגיה תרמית בתהליך, ותעלה טמפרטורת המערכת הקרה בהתאם. זרימת החום תיפסק בהגעה לשיווי משקל תרמודינמי, שיתקיים כאשר תגענה המערכות לשוויון טמפרטורות.

התנאי לשיווי משקל תרמודינמי

מערכת A נמצאת בצימוד תרמי עם מערכת B. שתי המערכות יחד מהוות מערכת סגורה, כלומר אינן מחליפות אנרגיה עם הסביבה או עם מערכת אחרת. הנפח ומספר החלקיקים של כל מערכת נשארים קבועים. משימור אנרגיה כוללת של שתי המערכות יחד מתקיים: $U=U_A+U_B=Const$.

נראה כי התנאי לשיווי משקל תרמודינמי הוא שוויון טמפרטורות בין המערכות בשתי דרכים, תוך שימוש בשיקולים שונים:

משמאל: שתי מערכות לפני צימוד תרמי. מימין: המערכות לאחר צימוד תרמי והגעה לשיווי משקל תרמודינמי. המסגרת החיצונית ממחישה בידוד תרמי מהסביבה.

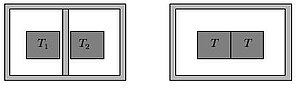
שיווי משקל משיקולי פונקציות תרמודינמיות

נסתכל על האנטרופיה הכוללת של שתי המערכות: $S=S_A+S_B$. התנאי לשיווי משקל הוא מקסימום של האנטרופיה הכוללת: $dS=0$.

מהחוק הראשון של התרמודינמיקה, תוך שמירת הנפח ומספר החלקיקים של כל מערכת קבועים, נקבל: $dS={\left(\frac{\partial S_A}{\partial U_A}\right)}_{V_A,N_A}d{U}_A+{\left(\frac{\partial S_B}{\partial U_B}\right)}_{V_B,N_B}d{U}_B$

נשתמש בהגדרת הטמפרטורה: $\frac{1}{T}=(\frac{\partial S}{\partial U}{)}_{V,N}$, ונקבל: $dS={\frac{1}{T}}_{A}d{U}_A+{\frac{1}{T}}_{B}d{U}_B$

משימור אנרגיה כוללת מתקיים: $d{U}_B=-d{U}_A$, לכן: $dS=({\frac{1}{T}}_A-{\frac{1}{T}}_B)d{U}_A$

מכאן ניתן לראות שהדרישה $dS=0$ שקולה לדרישה: $\Leftarrow {\frac{1}{T}}_A={\frac{1}{T}}_B$ שיווי משקל תרמודינמי יתקיים עבור $T_A=T_B$.

שיווי משקל משיקולי פיזיקה סטטיסטית

נסתכל על פונקציית הריבוי $g(U,V,N)$ של המערכת הסגורה, המתארת את מספר המצבים המיקרוסקופיים הזמינים המתאימים למצב מקרוסקופי מסוים;

המערכות בלתי תלויות (מלבד האילוץ של שימור אנרגיה כוללת), לכן משיקולי קומבינטוריקה ניתן לכתוב את פונקציית הריבוי הכוללת כמכפלת פונקציות הריבוי של כל אחת מהמערכות, תוך סכימה על אנרגיות $U_A,U_B$ אפשריות שונות:

$g_{tot}=\sum _{U_A,U_B}{g}_A\cdot g_B=\sum _{U_A,U_B}{g}_A(U_A,V_A,N_A)\cdot g_B(U_B,V_B,N_B)$

משימור אנרגיה כוללת במערכת הסגורה מתקיים:

$g_{tot}=\sum _{0\le U_A\le U}{g}_A(U_A,V_A,N_A)\cdot g_B(U-U_A,V_B,N_B)$

באדום: גאוסיאן בעל שיא צר, המאפיין את פונקציית הריבוי סביב נקודת שיווי המשקל. מרבית התרומה מתקבלת בטווח צר סביב השיא. בכחול: גאוסיאן בעל שיא רחב יותר. התרומה נפרשת על פני טווח רחב יותר סביב השיא.

מצב שיווי המשקל הוא המצב המקרוסקופי עבורו קיים מספר מקסימלי של מצבים מיקרוסקופיים זמינים: $d{g}_{tot}=0$. מקסימום זה מאופיין בשיא צר, כך שניתן להזניח את תרומת המצבים המקרוסקופיים האחרים לפונקציית הריבוי הכוללת. הנפח ומספר החלקיקים של כל מערכת נותרים קבועים, לכן (תוך שימוש בנגזרת מכפלה) נקבל: $d{g}_{tot}=g_B{\left(\frac{\partial g_A}{\partial U_A}\right)}_{V_A,N_A}d{U}_A+g_A{\left(\frac{\partial g_B}{\partial U_B}\right)}_{V_B,N_B}d{U}_B$

משימור אנרגיה כוללת מתקיים: $d{U}_B=-d{U}_A$, לכן:

$d{g}_{tot}=g_B{\left(\frac{\partial g_A}{\partial U_A}\right)}_{V_A,N_A}d{U}_A-g_A{\left(\frac{\partial g_B}{\partial U_B}\right)}_{V_B,N_B}d{U}_A$

מכאן ניתן לראות שהדרישה $d{g}_{tot}=0$ שקולה לדרישה:$\frac{1}{g_A}{\left(\frac{\partial g_A}{\partial U_A}\right)}_{V_A,N_A}=\frac{1}{g_B}{\left(\frac{\partial g_B}{\partial U_B}\right)}_{V_B,N_B}\iff g_B{\left(\frac{\partial g_A}{\partial U_A}\right)}_{V_A,N_A}=g_A{\left(\frac{\partial g_B}{\partial U_B}\right)}_{V_B,N_B}$

$\Leftarrow$ מתכונות נגזרת לוגריתם, שיווי משקל תרמודינמי יתקיים עבור: ${\left(\frac{\partial log(g_A)}{\partial U_A}\right)}_{V_A,N_A}={\left(\frac{\partial log(g_B)}{\partial U_B}\right)}_{V_B,N_B}$

נגדיר את האנטרופיה חסרת הממדים: $\sigma (U,V,N)\equiv log(g(U,V,N))$, המקיימת $S=k_B\sigma$ כאשר $k_B$ הוא קבוע בולצמן,

ונקבל כי בשיווי משקל: ${\left(\frac{\partial {\sigma }_A}{\partial U_A}\right)}_{V_A,N_A}={\left(\frac{\partial {\sigma }_B}{\partial U_B}\right)}_{V_B,N_B}$

בנוסף, נגדיר את הטמפרטורה: $\frac{1}{T}\equiv k_B{\left(\frac{\partial \sigma }{\partial U}\right)}_{V,N}$ ונקבל: $\Leftarrow {\frac{1}{T}}_A={\frac{1}{T}}_B$ שיווי משקל תרמודינמי יתקיים עבור $T_A=T_B$.

כיוון זרימת החום

נראה כי חום יזרום מהמערכת החמה למערכת הקרה עד ההגעה לשיווי משקל:

נניח שרירותית כי חום זרם ממערכת A למערכת B $d{U}_A=-d{U}_B<0\Leftarrow$. נסתכל על השינוי באנטרופיה הכוללת:

$dS=\frac{1}{T_A}d{U}_A+\frac{1}{T_B}d{U}_B=(\frac{1}{T_A}-\frac{1}{T_B})d{U}_A$

בשיווי משקל תרמודינמי האנטרופיה מקסימלית (וכן אינה יכולה לקטון בתהליך ספונטני) $dS\ge 0\Leftarrow$, בפרט כיוון שההנחה היא שזרם חום בין המערכות אזי $dS>0$,

אבל הנחנו כי $d{U}_A<0$, לכן בהכרח מתקיים $T_A>T_B\Leftarrow {\frac{1}{T}}_A<{\frac{1}{T}}_B$.

קיבלנו כי חום אכן זורם מהמערכת החמה למערכת הקרה, עד אשר מתקיים שוויון טמפרטורות.

ראו גם

• הולכת חום
• פונקציית ריבוי
• אנטרופיה
• שיווי משקל תרמודינמי
• תרמודינמיקה
• פיזיקה סטטיסטית

לקריאה נוספת

• Herbert B. Callen, Thermodynamics and an Introduction to Thermostatistics, Second Edition, University of Pennsylvania, John Wiley & Sons,1985
• Enrico Fermi, Thermodynamics, Dover, 1936
• C.J. Adkins, Equilibrium Thermodynamics, 3rd Edition, Cambridge University Press, 1983
• Charles Kittel and Herbert Kroemer, Thermal Physics, University of California, W.H. Freeman and Company, 1980
• David Goodstein, Thermal Physics, Cambridge University Press, 2015

הערות שוליים

קטגוריות:

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

שגיאות פרמטריות בתבנית:מיון ויקיפדיה
שימוש בפרמטרים מיושנים [ דרגה ] צימוד תרמי29111545