מומנט הדיפול של פלורופור

פלורופור (כרומופור של חלבון פלואורסצנטי ירוק) בעל מומנט דיפול המשתנה בהתאם למצבו האנרגטי. כיוון הדיפול הוא מהאזור השלילי במולקולה לאזור החיובי, בהתאם לאלקטרושליליות של האטומים המרכיבים את המולקולה.

בפיזיקה כימית, מומנט הדיפול של פלורופור מאפיין קוטביות חשמלית מולקולרית של הרכב כימי פלואורסצנטי ברמת אנרגיה מסוימת, בדרך כלל כאשר הוא נתון בתמיסה ואינו מהווה את הממס. מומנט הדיפול של פלורופור מסומן ב- $\mu$ או ב- ${\mu }_S$ כאשר $S$ היא הרמה האנרגטית של הפלורופור. לאינטראקציה בין הפלורופור לממס השפעה רבה על התכונות הספקטראליות של הפלורופור. ישנן כמה גישות לתיאור אינטראקציה זו, כאשר העיקרית שבהן מייחסת לפלורופור מרחב כדורי אפקטיבי עם מקדם דיאלקטרי נתון. במקרה כזה, משוואת ליפרט-מטגה מסבירה באופן חלקי את אפקט הקוטביות החשמלית של הפלורופור, אך לא לוקחת בחשבון כל אינטראקציה כימית חיצונית כאשר קיימת אחת כזו. בכל מקרה, האינטראקציה הכללית בין פלורופור לממס היא נושא יחסית מורכב ואיננו מוסבר באופן מלא על ידי תאוריה יחידה.

מצבים אנרגטיים של פלורופור בתמיסה

דיאגרמת יבלונסקי של פלורופור בתהליך עירור וחזרה למצב היסוד. פלורופור A מעורר למצב הסינגלט המעורר *1A, ומשם מתייצב לרמה נמוכה יותר (חצייה בין-מערכתית לרמת הטריפלט 3A). לאחר זמן מסוים (זמן החיים של הפלואורסצנציה), ישנה דעיכה קרינתית (הפוספורסצנציה של המולקולה הפלואורסצנטית) אל מצב היסוד.

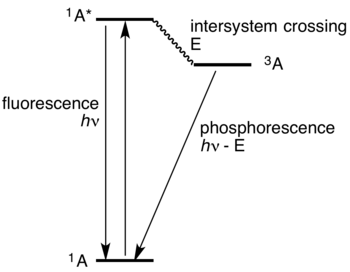
פלורופור הנתון בתמיסה מושפע ממנגנונים היכולים לגרום לעירור אנרגטי, למשל עירור תרמי. העירור התרמי והתדירות בה הוא מתרחש תלויים בטמפרטורת התמיסה. דרך נוספת לעורר פלורופור היא על ידי הקרנת פוטון בעל אורך גל השייך לספקטרום הבליעה של הפלורופור. במקרה כזה, הפוטון יכול להיבלע על ידי הפלורופור ולעוררו ברמת האנרגיה, בדרך כלל מרמת היסוד אל רמה ויברציונית כלשהי של $S_1$. בליעת האור על ידי הפלורופור איננה איזוטרופיות. ההסתברות לבליעה של פוטון על ידי הפלורופור תלויה בכיוונו של מרכיב השדה החשמלי של אותו פוטון ביחס לכיוונו של מומנט הדיפול של הפלורופור. כאשר כיוונו של השדה החשמלי מקביל לכיוונו של $\overrightarrow{\mu }$, מתקיימת בליעה מקסימלית, ובלבד שאורך הגל של הפוטון המוקרן שייך לספקטרום הבליעה של הפלורופור. כאשר כיוונים אלו מאונכים זה לזה, לא תהיה בליעה כלל. לאחר עירור של הפלורופור (בכל דרך שהיא), נניח אל אחת הרמות הויברציונית של $S_1$, הפלורופור מתייצב על רמת טריפלט (בין $S_0$ ל- $S_1$). הזמן בו הפלורופור נמצא באותו מצב טריפלט נקרא זמן החיים של הפלואורסצנציה ובתום זמן זה הפלורופור חוזר למצב היסוד תוך פליטת פוטון.

עירור אופטי ומשוואת ליפרט-מטגה

במקרה של עירור אופטי, מודל ליפרט-מטגה מתאר (בקירוב) בצורה יחסית פשוטה את האינטראקציה של הפלורופור בממס עם השדה האלקטרומגנטי. כאשר פלורופור ממוקם באזור בו שורר שדה אלקטרומגנטי, אלקטרונים של מולקולת הפלורופור נמצאים באינטראקציה עם השדה החשמלי של האור. אלקטרונים אלו מוגבלים לתנועה במרחב המולקולה, אך קיים כיוון מסוים בו תנועת האלקטרונים חופשית יותר. זהו כיוונו של מומנט הדיפול החשמלי $\overrightarrow{\mu }$ של הפלורופור. האינטראקציה בין הממס לפלורופור משפיעה על הפרשי רמות האנרגיה בהן יכול להימצא הפלורופור. כאשר פלורופור נמצא במצב האנרגטי הנמוך שלו, הוא בעל מומנט דיפול קבוע (בערכו) שכיוונו נקבע על ידי הרוטציה המרחבית. כאשר מקרינים את הפלורופור בספקטרום הבליעה שלו, הפלורופור יכול לעלות ברמת האנרגיה וכתוצאה ממנגנונים דינמיים הכרוכים בכך הוא משנה את מומנט הדיפול שלו. מומנט זה הוא מומנט דיפול מולקולרי זמני, וערכו ברמה המעוררת בדרך כלל גבוה יותר מאשר ערכו במצב היסוד. זמן קצר לאחר שהפלורופור מתקבע על מומנט הדיפול ברמה המעוררת, הוא חוזר למצב היסוד תוך פליטת פוטון באורך גל ארוך יותר מאורך הגל של הפוטון הנבלע. הפער בין אורכי הגל קיים כיוון שתהליך הפליטה של האור מהפלורופור איננו אלסטי והמנגנונים הדינמיים אשר היו כרוכים בו פיזרו אנרגיה שאינה קרינתית, כך שאנרגיית הפוטון הנפלט נמוכה יותר. הקשר בין אורכי הגל, הנבלע והנפלט, ניתן לתיאור בקירוב על ידי משוואת ליפרט-מטגה. משוואת ליפרט-מטגה מתארת בקירוב את התלות של היסט סטוקס במאפייני החומר ובמומנט הדיפול של הפלורופור. ההפרש (בקירוב) בין מספרי הגל הנבלע והגל הנפלט מפלורופור לפי מודל משוואת ליפרט-מטגה הוא:

$v_A-v_F=\frac{2}{hc}(\frac{\epsilon -1}{2\epsilon +1}-\frac{n^2-1}{2n^2+1})\frac{{({\mu }_E-{\mu }_G)}^2}{a^3}+Const$

כאשר $v_A$ ו- $v_F$ הם בהתאמה מספרי הגל הנבלע והגל הנפלט, $h$ הוא קבוע פלאנק, $c$ היא מהירות האור, $\epsilon$ ו- $n$ הם בהתאמה המקדם הדיאלקטרי ומקדם השבירה של המסס, $a$ הוא הרדיוס האפקטיבי של הפלורופור, ${\mu }_G$ ו- ${\mu }_E$ הם בהתאמה מומנטי הדיפול של הפלורופור במצב היסוד ובמצב המעורר, והקבוע שנותר תלוי בערכו של היסט סטוקס הלא מופרע (של הפלורופור בריק). בתיאור הנ"ל מניחים כי הפלורופור המעורר איננו משנה את כיוון מומנט הדיפול ביחס למצב הקודם, אלא רק את גודל המומנט. אולם, ישנם מקרים שהנחה זו איננה מתקיימת. במצבים כאלו ניתן להשתמש במשוואה דומה עבור היסט סטוקס כאשר הזווית בין מומנטי הדיפול היא $\alpha$ ואז מתקיים בקירוב הקשר:

$\mathrm{\Delta }v=\frac{2}{{\left(hc\right)}^2{a}^3}\cdot \frac{2n^2+1}{n^2+2}\cdot (\frac{\epsilon -1}{2\epsilon +1}-\frac{n^2-1}{2n^2+1})({\mu }_E^2-{\mu }_G^2-{\mu }_E{\mu }_G\cos \left(\alpha \right))+Const$

כאשר $\mathrm{\Delta }v=v_A-v_F$.

ראו גם

• פלואורסצנציה
• דיפול
• פלורופור

לקריאה נוספת

• Joseph R. Lakowicz (2006) Principles of Fluorescence Spectroscopy (3ed), Springer

קישורים חיצוניים

יהויכין מילר, פולריזציה של פלורופור (עמ' 8-24), ‏2006-06-08 (באנגלית)