רציפות למחצה

פרק זה טעון שכתוב. אנא תרמו למכלול ועזרו לשכתב אותו. הסיבה היא אין הגדרה ואין שימושים.

פונקציה רציפה למחצה עליונה

פונקציה רציפה למחצה תחתונה

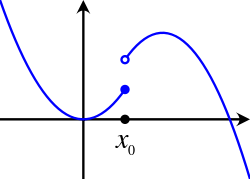
באנליזה מתמטית, רציפות למחצה היא מאפיין לפונקציות ממשיות שהוא יותר חלש מרציפות. רציפות למחצה יכולה להיות רציפות למחצה עליונה או תחתונה בנקודה $x_0$ אם בנקודות סמוכות היא רציפה אבל היא בעלת הפרדה בין שני חלקים באותה נקודה.

דוגמאות

• הפונקציה $f(x)=\{\begin{array}{ll}-1& :x<0\\ 1& :x\ge 0\end{array}$ היא רציפה למחצה עליונה בנקודה $x=0$ .
• פונקציית הערך השלם $\lfloor x\rfloor$ היא רציפה למחצה עליונה בכל נקודה שלמה.

פונקציה יכולה להיות רציפה למחצה אבל לא רציפה באותה נקודה.

• הפונקציה $f(x)=\{\begin{array}{ll}1& :x<1\\ 2& :x=1\\ \frac{1}{2}& :x>1\end{array}$ רציפה למחצה עליונה בנקודה $x=1$ אך לא רציפה באותה נקודה מפני שגבולותיה מימין ומשמאל שונים.
• הפונקציה $f(x)=\{\begin{array}{ll}\sin \left(\frac{1}{x}\right)& :x\ne 0\\ 1& :x=0\end{array}$ רציפה למחצה עליונה בנקודה $x=0$ כאשר הגבול הימני או השמאלי שלה לא קיים.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0