אופטימיזציית הגחלילית

אופטימיזציית הגחלילית (באנגלית: Firefly optimization) היא שיטה מטה-היוריסטית מתחום הבינה המלאכותית לאופטימיזציה של פונקציות המקבלת את השראתה מהתנהגותן של גחליליות בטבע. השיטה הוצעה על ידי קסין שי יאנג בשנת 2008, והיא שימושית בתחומים רבים, לרבות בעיבוד תמונה, תזמון תהליכים, ניתוח מבני של חלבונים, קינימטיקה הפוכה ועוד. סיבוכיות האלגוריתם היא $O(t)$, כאשר $t$ הוא מספר האיטרציות שמבצע האלגוריתם.

הקדמה

בעיית אופטימיזציה

גחלילית מזן Photuris lucicrescens

ערך מורחב – אופטימיזציה (מתמטיקה)

בעיית אופטימיזציה היא בעיה מתמטית העוסקת במציאת ערך אופטימלי (מינימלי או מקסימלי) עבור פונקציה נתונה, תחת אילוצים נתונים. כל בעיית אופטימיזציה ניתנת לתיאור ע"י:

${\begin{aligned}&{\text{optimize}}&&f(x)\\&{\text{subject to}}&&\mathbf {x\in S} \\\end{aligned}}$

כאשר ${\text{S}}$ היא קבוצת הפתרונות האפשריים לבעיה. $s$ הוא פתרון לבעיה אם ורק אם מתקיים $s\in S$ וגם $f(x)\leq f(s)$ לכל $x\in S$.

הגחליליות בטבע

ערך מורחב – גחליליות

הגחלילית (שם מדעי: Lampyridae) היא זן של חיפושית לילית. הגחלילית משתמשת בהבזקי אור כאמצעי תקשורת עם בני המין השני במהלך תהליך החיזור. זכר גחלילית הנמצא בתהליך החיזור מפיק הבזקי אור בזמן מעופו. נקבת הגחלילית הנענית לחיזור מפיקה גם היא אותות מיוחדים על מנת לסמן לזכר המחזר את מיקומה. עוצמתם ותדירותם של הבזקי האור הזכריים מעידים על האיכות הגנטית שלו, ומשפיעים על תגובתה של הנקבה. הבזקי האור נוצרים בתהליך הביולומינסנציה המבוקר בעיקר על ידי החלבון לוציפראז.

ניתן לראות את תהליך החיזור הכולל של נחיל גחליליות כמעין תהליך חיפוש המשלב אקראיות, חיפוש מקומי וחיפוש גלובלי (אלגוריתם מטה-היוריסטי).

האלגוריתם

תיאור

בהינתן מספר איטרציות מרבי $t_{max}$, ניתן לתאר את האלגוריתם בצורה הכללית הבאה:

1. אתחל אוכלוסייה אקראית $x_{1},...,x_{n}$ של $n$ גחליליות על פני פונקציית מטרה $f(x)$ ב- $d$ ממדים, כאשר $f(x_{i})$היא עוצמת ההארה של גחלילית $x_{i}$.
2. לכל זוג גחליליות $x_{i},x_{j}$, אם גחלילית $x_{i}$ בהירה יותר מגחלילית $x_{j}$, הזז את גחלילית $x_{j}$ לכיוון גחלילית $x_{i}$ על פי משוואת התנועה: $\mathbf {x} _{i}^{t+1}=\mathbf {x} _{i}^{t}+\beta \exp[-\gamma r_{ij}^{2}](\mathbf {x} _{j}^{t}-\mathbf {x} _{i}^{t})+\alpha _{t}{\boldsymbol {\epsilon }}_{t}$ כאשר $t$ מייצג נקודה בזמן, $\ x_{i},x_{j}$ הן מיקום הגחליליות $i,j$ בהתאמה, $\alpha _{t}$ הוא מקדם אקראיות ו- ${\boldsymbol {\epsilon }}_{t}$ הוא וקטור מספרים אקראיים המתפלגים נורמלית בזמן $t$. אחרת, הזז את הגחלילית $x_{j}$ באופן אקראי.
3. עדכן את תאורת הגחליליות ואת מידת המשיכה בין הגחליליות ע"פ המיקומים והמרחקים החדשים שהתקבלו.
4. חזור על שלבים (2) ו- (3) למשך $t_{max}$ פעמים. בסיום, הגחלילית המוארת ביותר היא קירוב לפתרון הבעיה.

בבעיות למציאת מקסימום, יתקיים $I\propto f(\mathbf {x} )$ ובבעיות למציאת מינימום יתקיים $I\propto f^{-1}(x)$.

פסאודו - קוד

Begin
Generate a random population of n fireflies x_1, x_2, ..., x_n
While (t < MaxGeneration)
update distances
update lights intensities
update attractiveness
for i = 1 : n
for j = 1 : n
if (I_j > I_i),
move firefly i to j
end if
end for j
end for i
set s as the firefly with the optimal light intensity.
end while
return s as solution
end

רקע תאורטי

מודל מתמטי

האלגוריתם מבוסס על אידיאליזצית תכונות ההארה של מאור הגחליליות. הגחלילית, בקרב מרבית זני הגחליליות בטבע, משתמשת בהארה על מנת למשוך אליה פרטי להקה אחרים לצורכי זיווג. התכונות האידיאליות הן כדלקמן:

1. כל גחלילית נמשכת לגחליליות אחרות, ללא קשר למינן.
2. מידת המשיכה של גחלילית $a$ כלפי גחלילית $b$ היא ביחס ישר למידת ההארה של גחלילית $b$ (אנלוגיה להתנהגותן הטבעית של הגחליליות).
3. עוצמת האור שגחלילית $a$ קולטת מגחלילית $b$ היא ביחס הפוך למרחק בין גחלילית $a$ לבין גחלילית $b$ (אנלוגיה לחוק ריבוע המרחק ההופכי, לפיו עוצמת האור נחלשת ביחס ריבועי הפוך למרחק ממקור האור).
4. עוצמת ההארה של הגחלילית נקבעת ע"פ ערכה של פונקציית המטרה $f(x)$.

על פי תכונות (2) ו- (3), ניתן לגזור את משוואת המשיכה בין שתי גחליליות, כפונקציה מעריכית של המרחק ביניהן: $\beta =\beta _{0}e^{-\gamma r^{2}}$ כאשר $\beta _{0}$ הוא קבוע, $\gamma$ הוא מקדם התפשטות האור באוויר, $\beta$ היא עוצמת המשיכה בין שתי גחליליות ו- $r$ הוא המרחק הגאומטרי בין שתי הגחליליות. תנועתה של גחלילית $i$ מושפעת מגחלילית בהירה יותר $j$ באופן הבא:

$\mathbf {x} _{i}^{t+1}=\mathbf {x} _{i}^{t}+\beta \exp[-\gamma r_{ij}^{2}](\mathbf {x} _{j}^{t}-\mathbf {x} _{i}^{t})+\alpha _{t}{\boldsymbol {\epsilon }}_{t}$

כאשר $t$ מייצג נקודה בזמן, $\ x_{i},x_{j}$ הן מיקום הגחליליות $i,j$ בהתאמה, $\alpha _{t}$ הוא מקדם אקראיות ו- ${\boldsymbol {\epsilon }}_{t}$ הוא וקטור מספרים אקראיים המתפלגים נורמלית בזמן $t$. עבור $\beta _{0}=0$ מתקבלת תנועה אקראית פשוטה, ועבור $\gamma =0$ מתקבלת משוואת תנועת חלקיקים של אופטימיזציית הנחיל.

חלוקה אוטומטית

במקרים רבים, אלגוריתם הגחליליות יעיל יותר מאלגוריתמים רבים אחרים מתחום בינת הנחיל. סיבה עיקרית לכך היא תופעת החלוקה האוטומטית. האלגוריתם מבוסס על כך שאטרקטיביות של פתרון פוחתת עם עליית המרחק, ולכן, נוצר מצב שבו האוכלוסייה מופרדת באופן אוטומטי לתתי-קבוצות, כאשר כל תת-קבוצה מרוכזת סביב אופטימום מקומי שונה. עבור אוכלוסייה הגדולה מאוד ממספר מוקדי האופטימום המקומיים, חלוקה זו מאפשרת למצוא את כל המוקדים המקומיים בו-זמנית. מבחינה מתמטית, ${\sqrt {\gamma }}^{-1}$ מאפיין את המרחק הממוצע בין שתי קבוצות גחליליות סמוכות. מכאן, כל אוכלוסייה נחלקת לתתי קבוצות סמוכות בעלות מרחק ממוצע קבוע. עובדה זו מאפשרת התמודדות עם בעיות שאינן ליניאריות.

גרף של פונקציה 4-קוטבית

קל לזהות את תופעת החלוקה האוטומטית בהרצת האלגוריתם על הפונקציה התלת-מימדית הבאה:

$f(x,y)=e^{-x^{2}-y^{2}}({\left|x\right|}+{\left|y\right|})$

לפונקציה $f(x,y)$ ישנן ארבע נקודות מקסימום $(\pm 0.5,\pm 0.5)$. האלגוריתם מאפשר את מציאת הקטבים על ידי $25$ גחליליות ו- $20$ איטרציות. הסכימה הבאה מתארת את מיקומן האקראי של הגחליליות (כנקודות) בתחילתה של ריצת האלגוריתם (משמאל) ואת מיקומן בסיום ריצת האלגוריתם:

גרף של פונקציית רוזנברוק עבור n=2.

התמקדות כנגד התרחבות

רעיון כללי

שני המרכיבים העיקריים בכל שיטה מטה-היוריסטית הם התמקדות והתרחבות.

• התמקדות - חיפוש מקומי ממוקד בתחום שבו קיים פתרון אופטימלי מקומי. מידת התמקדות גבוהה נוטה להגדיל את קצב ההתכנסות של האלגוריתם, אך עשויה לגרום להתכנסות מקומית בלתי רצויה.
• התרחבות - חיפוש גלובלי הבוחן את כל הפתרונות האפשריים, תוך הימנעות מהתכנסות לפתרון אופטימלי מקומי. מידת התרחבות גבוהה נוטה להקטין את קצב ההתכנסות של האלגוריתם, אך מעלה משמעותית את ההסתברות למציאת אופטימום גלובלי.

אלגוריתם המחלק את פעולתו להתמקדות והתרחבות נקרא אלגוריתם חיפוש-לסירוגין. רמות ההתמקדות וההתרחבות של האלגוריתם, וכמו כן מידת האיזון בין שני המרכיבים, נקבעות על ידי מידת האקראיות וערכי הפרמטרים. יעילותו ודיוקו של האלגוריתם תלוי ביחס ההתמקדות-התרחבות $Q$:

$Q={\frac {\tau _{a}}{\tau _{b}}}$

כאשר $\tau _{a}$ ו- $\tau _{b}$ הם פרקי הזמן המנוצלים לתהליך ההתמקדות ולתהליך ההתרחבות, בהתאמה.

מציאת יחס התמקדות-התרחבות אופטימלי

חשיבותו של יחס התמקדות-התרחבות מוביל לפיתוח המודל התאורטי הבא, עבור המקרים הדו-ממדיים והתלת-ממדיים: אלגוריתם חיפוש המתמקד במרחב פתרונות קטן בעל רדיוס $a$ הנמצא במרחב פתרונות שרדיוסו $b$, כאשר $a\ll b$, ניתן למידול על ידי תהליך דיפוזיבי איטי המתואר על ידי מערכת המשוואות הסטוכסטיות הדיפרנציאליות הבאות:

$\left\{{\begin{matrix}D\nabla _{r}^{2}t_{1}+{\frac {1}{2\pi \tau _{a}}}\int _{0}^{2\pi }\left[t_{2}(r)-t_{1}(r)\right]d\theta +1=0\\\\u\nabla _{r}t_{2}(r)-{\frac {1}{\tau _{b}}}\left[r_{2}(r)-t_{1}(r)\right]+1=0\end{matrix}}\right.$

כאשר $D$ הוא קבוע הדיפוזיה, $\tau _{a}$ ו- $\tau _{b}$ הם תוחלות הזמן שנוצלו לתהליך ההתמקדות ולתהליך ההתרחבות, בהתאמה, $t_{1}$ ו- $t_{2}$ הם תוחלות זמני ההגעה למטרה בתהליך ההתמקדות ובתהליך ההתרחבות, בהתאמה, ו- $u$ הוא קצב החיפוש הממוצע. תחת ההנחה שקצב החיפוש $u$ זהה בכל הצעדים, פרק הזמן המינימלי הדרוש לכל אחד מהשלבים הוא:

$\tau _{a}^{\mathrm {min} }\approx {\frac {D}{2u^{2}}}\cdot {\frac {\ln ^{2}{\frac {b}{a}}}{2\ln {\frac {b}{a}}-1}}\quad \quad \tau _{b}^{\mathrm {min} }\approx {\frac {a}{u}}{\sqrt {\ln {\frac {b}{a}}-{\frac {1}{2}}}}$

כאשר $u\rightarrow \infty$, מתקבל יחס ההתמקדות-התרחבות האופטימלי:

$(1)\quad Q_{\mathrm {optimal} }={\frac {\tau _{a}}{\tau _{b}^{2}}}\approx {\frac {D}{a^{2}}}{\frac {1}{\left[2-{\frac {1}{\ln {\frac {b}{a}}}}\right]^{2}}}$

התוצאות לעיל קבילות עבור המקרה הדו-מימדי, ושלא קיימות תוצאות כלליות עבור יותר מ-3 ממדים.

דוגמה - מציאת יחס התמקדות-התרחבות אופטימלי של הילוך איזוטרופי

נדגים את חישוב יחס ההתמקדות-התרחבות במקרה דו-ממדי של הילוך אקראי איזוטרופי, כלומר, במצב שבו מתקיים:

$D\approx {\frac {s^{2}}{2}}$

כאשר $D$הוא קבוע הדיפוזיה ו-$s$ הוא אורך הצעד של המהלך בכל איטרציה. במקרה שבו $b/a\rightarrow \infty$ נקבל מתוצאה (1):

$Q_{\mathrm {optimal} }={\frac {\tau _{a}}{\tau _{b}^{2}}}\approx {\frac {1}{8}}$

מכאן ניתן להסיק שבמקרה זה, יש להשקיע זמן רב יותר בשלב ההתרחבות מאשר בשלב ההתמקדות.

דוגמה - מציאת יחס התמקדות-התרחבות אופטימלי של פונקציית גל עומד

גרף של גל הרמוני העומד על דיסק

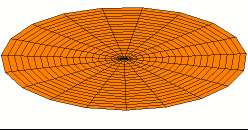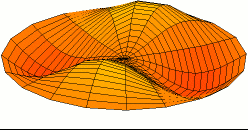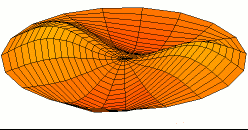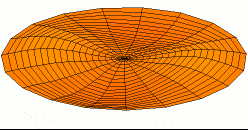
נדגים את חישוב יחס ההתמקדות-התרחבות במקרה של פונקציית גל-עומד:

$f(x)=1+\left\{\exp \left[-\sum _{i=1}^{d}\left({\frac {x_{i}}{\beta }}\right)^{10}\right]-2\exp \left[-\sum _{i=1}^{d}\left(x_{i}-\pi \right)^{2}\right]\right\}\cdot \prod _{i=1}^{d}\cos ^{2}x_{i}$

פונקציה זו מאופיינת במספר גדול של נקודות קיצון מקומיות, ובעלת מינימום גלובלית יחידה $f_{\mathrm {min} }=0$ בנקודה $(\pi ,\pi ,\dots ,\pi )$ בתחום $-20\leq x_{i}\leq 20$ כאשר $i=1,2,\dots ,d$ ו- $\beta =15$. נקבע ש- $\alpha =\pi /2$, ומכיוון ש- $b=20$, נובע ש- $b/a=12.7$, ועבור $d=2$נקבל:

$Q_{\mathrm {optimal} }\approx {\frac {1}{2\left[2-\ln \left({\frac {b}{a}}\right)\right]^{2}}}\approx 0.19$

מכאן ניתן להסיק, שבהפעלת האלגוריתם על פונקציית גל-עומד, על האלגוריתם להשקיע 80% מזמן החיפוש בהתרחבות ו- 20% מזמן החיפוש בהתמקדות, על מנת לבצע את החישוב בזמן אופטימלי.

הטבלה הבאה מתארת רצף של חמישה ניסויים, בהם מופעל אלגוריתם הגחליליות למציאת מינימום עבור פונקציית גל-עומד, כאשר $n=15$, $t=1000$, $x\in [-20,20]^{n}$, $\beta =15$ ו- $Q$ משתנה.

השוואה של ביצועי אלגוריתם הגחליליות מול האלגוריתם של בניצ'ו אטאל, עבור מספר ממדים משתנה.

$Q$	$0.4$	$0.3$	$0.2$	$0.1$	$0.05$
תוצאה	$9.4e-11$	$9.4e-11$	$9.4e-11$	$9.4e-11$	$9.4e-11$

קל להבחין שהתוצאה המדויקת ביותר מתקבלת כאשר $Q=0.2$ - הבחנה אמפירית המתלכדת עם הטענה התאורטית.

הכללה לממדים גבוהים

אלגוריתם החיפוש-לסירוגין אשר הוצע על ידי בניצ'ו אטאל עבור ממדים גבוהים יותר, מתבסס על היחסים האסימפטוטיים הבאים, המתקבלים באמצעות אקסטרפולציה:

${\frac {\tau _{a}}{\tau _{b}^{2}}}\sim O\left({\frac {D}{a^{2}}}\right)\quad \quad \tau _{m}\sim O\left({\frac {b}{u}}\left({\frac {b}{a}}\right)^{d-1}\right)$

כאשר $\tau _{m}$ הוא זמן החיפוש הכולל הממוצע. הודגם אמפירית כי בממדים גבוהים, אלגוריתם הגחליליות יעיל בהרבה מן האלגוריתם הנ"ל, אך לא נמצא מודל תאורטי המסביר את תוצאות הניסוי.

קביעת הפרמטרים

מקדם האקראיות $\alpha _{t}$ מווסת את מידת האקראיות של מהלכי הגחליליות. כיוון שהפחתה הדרגתית של מידת האקראיות תאפשר מניעה של התכנסות לאופטימום מקומי, התכנסות מהירה תתקבל עבור $\alpha _{t}=a_{0}\delta ^{t}$

כאשר $\delta \in [0,1]$ ו- $a_{0}$ הוא מקדם אקראיות התחלתי. סימולציות מראות שהתכנסות יעילה במיוחד מתקבלת עבור $\gamma =1/{\sqrt {L}}$, $n\in [25,40]$, $a_{0}=0.01L$, כאשר $L$ הוא סדר הגודל הממוצע של פתרונות הבעיה.

סיבוכיות זמן

סיבוכיות האלגוריתם היא $O(n^{2}t)$, כאשר $t$ הוא מספר האיטרציות ו- $n$ הוא מספר הגחליליות. עבור $n$ גדול יחסית, ניתן להחליף את הלולאה הכפולה בלולאה יחידה, ולמיין את מידת המשיכה של הגחליליות באמצעות אלגוריתם מיון השוואתי. במקרה זה, סיבוכיות האלגוריתם היא $O(nt\log {n})$. בשני המקרים, הסיבוכיות ליניארית ב- $t$.

הערכת ביצועים

להלן מספר האיטרציות שנדרשו לפתרון בעיות אופטימיזציה עבור שלוש פונקציות מרכזיות, בטווח נתון, וכתלות במספר הממדים של הפונקציה ($n$).

פונקציית ספירה (Sphere function)

גרף של פונקציית ספירה עבור n=2.

${\textrm {Sphere}}({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}\quad \quad [-100,100]^{n}$

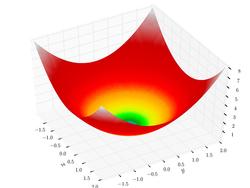
$n$	מינימום	מקסימום
15	6239	6440
30	6202	6452
60	6149	6398

פונקציית אקליי (Ackley function)

גרף של פונקציית אקליי עבור n=2.

${\textrm {Ackley}}({\boldsymbol {x}})=-20\exp \left[-{\frac {1}{5}}{\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}{x_{i}^{2}}}}\right]-\exp \left[{\frac {1}{n}}\sum _{i=1}^{n}{\cos(2\pi x_{i})}\right]+20+e\quad \quad [-30,30]^{n}$

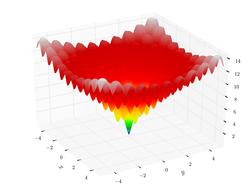
$n$	מינימום	מקסימום
15	1720	2176
30	1568	1805
60	1402	1862

פונקציית רוזנברוק

גרף של פונקציית רוזנברוק עבור n=2.

${\textrm {Rosenbrock}}({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right]\quad \quad [-30,30]^{n}$

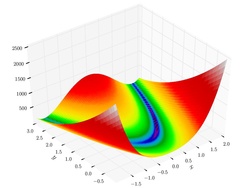
$n$	מינימום	מקסימום
15	2497	2938
30	2531	2653
60	2471	2574

שימושים עיקריים

• בעיבוד תמונה, קוונטיזצייה וקטורית המשמשת לדחיסה דיגיטלית של תמונות ורגיסטרציה של תמונות קשיחות.
• במתמטיקה, אופטימיזציית ערכים עצמיים של מערכות איזו-ספקטרליות ואופטימיזצייה פרמטרית עבור מכונת וקטורים תומכים.
• בשידור, תכנון אנטנות.
• בהנדסת מבנים, אופטימיזציית בבעיות מרובות משתנים.
• במדעי המחשב, פתרון יעיל לבעיית הסוכן הנוסע ולבעיות תחביר סמנטיות.
• בכימיה, ניתוח מצבי שיווי משקל.
• בביולוגיה, ניבוי של מבני חלבונים.

ראו גם

• אופטימיזציית הנחיל
• בינה מלאכותית
• אלגוריתם קן הנמלים
• תנועה בראונית

לקריאה נוספת

1. Yang, X. S. (2008). Nature-Inspired Metaheuristic Algorithms. Frome: Luniver Press. מסת"ב 1-905986-10-6
2. Yang, X. S. (2009). "Firefly algorithms for multimodal optimization". Stochastic Algorithms: Foundations and Applications, SAGA 2009. Lecture Notes in Computer Sciences 5792. pp. 169–178. arXiv:1003.1466.

קישורים חיצוניים

• Google Code Archive - Long-term storage for Google Code Project Hosting., code.google.com
• מימוש לאלגוריתם הגחליליות ב- Python
• מימוש לאלגוריתם הגחליליות ב- C
• מימוש לאלגוריתם הגחליליות ב- Mathlab

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

30399982אופטימיזציית הגחלילית