בסיס אונארי
ספירה על בסיס אונרי היא בסיס ספירה לפי 1. זו שיטת הספירה הפשוטה ביותר לייצוג המספרים הטבעיים: כדי לייצג מספר טבעי כלשהו - N, סמל כלשהו יחזור על עצמו N פעמים. לדוגמה: על ידי שימוש בסימן | (קו אנכי), המספר 6 מיוצג על ידי שישה קווים אנכיים ||||||. דוגמה נפוצה לספירה באמצעות בסיס אונרי, היא ספירה באמצעות אצבעות הידיים.
מידע כללי
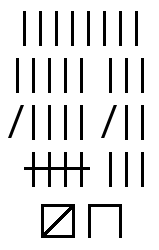
לרוב נהוג לקבץ את הסימנים בקבוצות של 5 (למשל, על ידי מתיחת קו על כל ארבעה סימנים) לצורך שיפור הקריאות, בדומה לשימוש בפסיקים הנפוץ בשיטה העשרונית כדי להפוך מספרים גדולים דוגמת 100,000,000 לקריאים יותר.
חיבור וחיסור הם פשוטים למדי בשיטה האונרית - כדי לחבר שני מספרים פשוט צריך לצרף את סדרות הסימנים שמייצגות את שני המספרים יחד. כדי לבצע חיסור די לכתוב את המחוסר מעל המחסר ולמחוק את החלק המשותף. לעומת זאת, חילוק וכפל הם מסובכים וקשים יותר לביצוע.
בשיטה האונרית אין סימן מוסכם המשמש לייצוג אפס כפי שקיים בבסיסי הספירה האחרים - אם הייתה ספרה עבור אפס, הבסיס היה למעשה בינארי, שכן היה מכיל שתי ספרות. לכן לאפס מתייחסים בצורה עקיפה, על ידי אי כתיבת מספר במקום שבו מצפים שיופיע. הדבר אינו ייחודי לשיטה האונרית - גם בשיטות ספירה מתקדמות יחסית דוגמת הספרות הרומיות אין סימן לאפס.
בהשוואה לשיטות ספירה המבוססות על מיקום, שיטת הספירה האונרית היא מסורבלת ולא משתמשים בה עבור חישובים גדולים. עם זאת, לעיתים משתמשים בה במדעי המחשב כאשר מדברים על מחלקות סיבוכיות, הסיבה היא שבבסיס אונארי, על מנת לייצג את המספר N - דרושים לנו N תווים, בעוד שבשביל להציג את המספר N בכל בסיס אחר שאינו אונארי, דרושים לנו c*logN תווים, כאשר c הוא קבוע שתלוי בבסיס שנבחר (אך לא ב-N), ההבדל הגדול בין כמות התווים בין בבסיס אונארי לעומת בסיסים אחרים משמש אותנו על מנת לבצע אבחנות לגבי המשאבים שבעיה מסוימת עלולה לדרוש על מנת לפתור אותה, לדוגמה אם האלגוריתם שלנו מקבל כקלט מספר טבעי N ומבצע N צעדים, אזי אם הקלט יכתב בבינארית, מספר הצעדים שהאלגוריתם יעשה הוא מעריכי בגודל הייצוג של הקלט (שכן אנו זקוקים ל־logN תווים והאלגוריתם ביצע N צעדים), ואם הקלט יכתב באונארית, מספר הצעדים שהאלגוריתם יעשה הוא ליניארי בגודל הייצוג של הקלט, השאלה "איך אנחנו מגדירים לפי איזה בסיס נייצג מספרים" תלויה בבעיה, והיא חלק מהגדרת הבעיה, לעיתים אנו נתקלים בבעיות שנחשבות קשות לפתרון (במובן של כמות משאבים גבוהה) ואז מסתכלים על ה"גרסה האונארית" של הבעיה, בה כל מספר מיוצג בבסיס אונארי, ומגלים שאותו אלגוריתם בדיוק שפעל מקודם בסיבוכיות מעריכית, פועל כעת בסיבוכיות פולינומית, נשים לב שהבעיה עצמה לא השתנתה, וגם לא האלגוריתם, פשוט שינינו את "חוקי המשחק" על ידי הגדרה של איך אנחנו מייצגים את הקלטים, וההחלטה הזו היא חלק מהגדרת הבעיה.
לדוגמה, הבעיה של פירוק מספר לגורמים דורשת, ככל הידוע, זמן ריצה שהוא יותר מאשר פולינומי בגודל הקלט כאשר הקלט הוא מספר הנתון בבסיס בינארי, וגודל הקלט נמדד על פי מספר הספרות (ולכן הוא לוגריתם על בסיס 2 של המספר עצמו שהועבר). לעומת זאת, אם המספר יועבר בבסיס אונרי, זמן הריצה יהיה ליניארי בגודל הקלט (שיהיה שווה במקרה זה לגודל המספר). בצורה זו לא נחסך זמן, אלא פשוט נבחרת דרך אחרת למדוד בה את הסיבוכיות של הבעיה.
ראו גם
קישורים חיצוניים
| בסיסי ספירה | |
|---|---|
|
בסיס אונארי39283829Q724775


