משפט נפוליאון

משפט נפוליאון
מידע כללי
תחום	גאומטריה אוקלידית
נקרא על שם	נפוליאון בונפרטה
ניסוח	מרכזי הכובד של משולשים שווי-צלעות הנחים על משולש כללי ופונים כולם החוצה/פנימה, יוצרים משולש שווה-צלעות
הקשר
גרסאות חזקות יותר	משפט פטר-דאגלס-ניומן
כלים בהוכחה	טריגונומטריה, המישור המרוכב

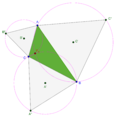
משפט נפוליאון הוא משפט גאומטרי הקובע כי בהינתן משולש כלשהו שעל צלעותיו בונים משולשים שווי-צלעות, כך שכולם אל מחוץ למשולש או לתוכו, מרכזי הכובד (שהם מפגשי התיכונים) של המשולשים שווי-הצלעות יוצרים משולש שווה-צלעות.^[1]

משולשים אלו, שקודקודיהם הם מרכזי הכובד של המשולשים שנבנו על הצלעות, מכונים משולשי נפוליאון (הפנימי והחיצוני, בהתאמה).

הקונפיגורציה המתקבלת מן המשפט מקיימת תכונות נוספות. למשל, שלושת המעגלים החוסמים את המשולשים שנבנו על צלעות המשולש המקורי נפגשים בנקודה אחת. קודקודיו של משולש נפוליאון הפנימי נמצאים על המעגלים החוסמים את המשולשים שווי הצלעות החיצוניים (ולהפך). ההפרש בין שטח משולש נפוליאון החיצוני לבין שטח משולש נפוליאון הפנימי שווה לשטח המשולש המקורי.

המשפט קרוי על שם נפוליאון בונפרטה, קיסר צרפת בראשית המאה ה-19, אם כי הדעות חלוקות האם הוא מי שגילה או הוכיח אותו.^[2]

נוסח המשפט

יהי משולש כלשהו $△ A B C$ . בונים על גבי הצלעות $A B$ , $A C$ ו- $B C$ שלושה משולשים שווי-צלעות $△ A B C^{'}$ , $△ A C B^{'}$ ו- $△ B C A^{'}$ בהתאמה, כך ששלושת המשולשים הללו פונים החוצה מן המשולש $△ A B C$ .

מסמנים ב- $L$ , $M$ ו- $N$ את מרכזי הכובד של המשולשים $△ A B C^{'}$ , $△ A C B^{'}$ ו- $△ B C A^{'}$ בהתאמה.

אזי, המשולש $△ L M N$ הוא משולש שווה-צלעות. משולש זה נקרא משולש נפוליאון החיצוני.

הוכחות

הוכחה טריגונומטרית

מסמנים:

$∠ B A C = α$ , $∠ A B C = β$ ו- $∠ A C B = γ$
$B C = a$ , $A C = b$ ו- $A B = c$

מסמנים ב- $S$ את שטח המשולש $△ A B C$ . לפי נוסחת שטח משולש על בסיס זוג צלעות והזווית ביניהן, מתקבל ש:

$S = \frac{1}{2} a b \sin γ = \frac{1}{2} a c \sin β = \frac{1}{2} b c \sin α$

בנוסף, מסמנים $P : = a^{2} + b^{2} + c^{2}$ .

מרכז הכובד של משולש נמצא בנקודת מפגש התיכונים שלו. מכיוון שבמשולש שווה צלעות כל התיכונים הם גם חוצי הזווית, ניתן להסיק שהזווית $∠ C A M$ ו- $∠ B A L$ שוות ל- $3 0^{\circ}$ .

בנוסף, מכיוון במשולש שווה צלעות התיכונים הם גם אנכים, ניתן להשתמש במשפט פיתגורס ובעובדה שהתיכונים חוצים זה את זה ביחס של $2 : 1$ כדי לקבל ש- $A M = \frac{1}{\sqrt{3}} b$ ו- $A L = \frac{1}{\sqrt{3}} c$ .

לבסוף, לפי משפט הקוסינוסים על המשולש $△ A B C$ , מתקיים ש- $\cos α = \frac{b^{2} + c^{2} - a^{2}}{2 a b}$ .

כעת, ניתן להשתמש במשפט הקוסינוסים על המשולש $△ M A L$ ולקבל:

$\begin{aligned} M L^{2} = A M^{2} + A L^{2} - 2 A M \cdot A L \cdot \cos (∠ M A L) \\ = \frac{1}{3} b^{2} + \frac{1}{3} c^{2} - \frac{2}{3} b c \cos (α + 6 0^{\circ}) \\ = \frac{1}{3} b^{2} + \frac{1}{3} c^{2} - \frac{2}{3} b c (\cos (6 0^{\circ}) \cos α - \sin (6 0^{\circ}) \sin α) \\ = \frac{1}{3} b^{2} + \frac{1}{3} c^{2} - \frac{2}{3} b c (\frac{1}{2} \cdot \frac{b^{2} + c^{2} - a^{2}}{2 b c} - \frac{\sqrt{3}}{2} \sin α) \\ = \frac{1}{6} (a^{2} + b^{2} + c^{2}) + \frac{1}{\sqrt{3}} b c \sin α \\ = \frac{1}{6} P + \frac{2}{\sqrt{3}} S \end{aligned}$

(בחישוב לעיל נעשה שימוש בזהות הטריגונומטרית הנוגעת לקוסינוס של סכום זוויות).

חישוב דומה על הצלעות $N M$ ו- $L M$ יראה שגם הן שוות ל- $\sqrt{\frac{1}{6} P + \frac{2}{\sqrt{3}} S}$ . על כן, המשולש $△ L M N$ הוא שווה צלעות.^[3]

מ.ש.ל.

הוכחה באמצעות המישור המרוכב

משכנים את הדיאגרמה של הבעיה במישור המרוכב. מגדירים $j : = e^{i \frac{2 π}{3}} = - \frac{1}{2} + \frac{\sqrt{3}}{2} i$ . $j$ זה מקיים את הזהויות $j^{3} = 1$ ו- $j^{2} + j + 1 = 0$ .

ניתן להוכיח כי במישור המרוכב, הנקודות $z_{1}, z_{2}, z_{3}$ מהוות משולש שווה-צלעות אם ורק אם מתקיים ש- $z_{1} + j z_{2} + j^{2} z_{3} = 0$ . מכיוון והמשולשים $△ A B C^{'}$ , $△ A C B^{'}$ ו- $△ B C A^{'}$ הם שווי צלעות, מתקיים ש: $A + j B + j^{2} C^{'} = 0$ , $C + j A + j^{2} B^{'} = 0$ ו- $B + j C + j^{2} A^{'} = 0$ .

לפי הנוסחה של מרכז כובד, מקבלים ש- $L = \frac{1}{3} (A + B + C^{'})$ , $M = \frac{1}{3} (A + C + B^{'})$ ו- $N = \frac{1}{3} (B + C + A^{'})$ .

מכאן מקבלים ש:

$\begin{aligned} M + j N + j^{2} L = \frac{1}{3} (A + C + B^{'}) + \frac{j}{3} (B + C + A^{'}) + \frac{j^{2}}{3} (A + B + C^{'}) \\ = \frac{1}{3} (\underset{⏟}{A + j B + j^{2} C^{'}} = 0 + j \underset{⏟}{(C + j A + j^{2} B^{'})} = 0 + j^{2} \underset{= 0}{\underset{⏟}{(B + j C + j^{2} A^{'})}}) = 0 \end{aligned}$

משמע שהמשולש $△ L M N$ הוא משולש שווה-צלעות.^[4]

מ.ש.ל.

משפט נפוליאון עבור משולשים הפונים פנימה

משפט נפוליאון מתקיים גם כאשר במקום להפנות את המשולשים שווי-הצלעות החוצה, מפנים אותם פנימה אל עבר המשולש המקורי.

ההוכחה של מקרה זה באמצעות שיכון במישור המורכב נשארת זהה, אך במקום להשתמש ב- $j = \frac{1}{2} - \frac{\sqrt{3}}{2} i$ , משתמשים ב- $j^{2} = - \frac{1}{2} - \frac{\sqrt{3}}{2} i$ , ששקול לסיבוב ב- $12 0^{\circ}$ בכיוון ההפוך מ- $j$ .

המשולש שווה-הצלעות הנוצר משלושת משלושת מרכזי הכובד נקרא משולש נפוליאון הפנימי.

חישוב דומה לזה של משולש נפוליאון החיצוני יוכיחו כי אורך הצלע של משולש זה היא $\sqrt{\frac{1}{6} P - \frac{2}{\sqrt{3}} S}$ (כאשר $P$ הוא סכום ריבועי אורכי צלעות המשולש המקורי ו- $S$ הוא שטח המשולש המקורי, כפי שהוגדרו בהוכחה הטריגונומטרית).

הנוסחה לחישוב שטח משולש-שווה צלעות היא $\frac{\sqrt{3}}{4} l^{2}$ , כאשר $l$ היא אורך צלע המשולש. חישוב של שטח משולשי נפוליאון החיצוני והפנימי יראה שהפרש השטחים הוא שטח המשולש המקורי $S$ .

אי-שוויון ויצנבק

כאמור לעיל, אורך הצלע של משולש נפוליאון הפנימי הוא $\sqrt{\frac{1}{6} P - \frac{2}{\sqrt{3}} S}$ . מאחר ומשולש נפוליאון הפנימי קיים עבור כל משולש כללי כלשהו, הביטוי שבתוך השורש הריבועי חייב להיות חיובי תמיד, אחרת השורש הוא בלתי מוגדר. אחרי העברת אגפים והכפלה בגורם משותף, מתקבל כי אי-השוויון $P \geq 4 \sqrt{3} S$ מתקיים לכל משולש כללי. זהו אי-שוויון ויצנבק (Weitzenböck's inequality) הקובע כי לכל משולש כלשהו, שטח המשולש קטן פי $4 \sqrt{3}$ מסכום שטחי הריבועים הנחים על צלעותיו.

אי-שוויון ויצנבק הופך לשוויון אם ורק אם רק המשולש הוא משולש-שווה צלעות. במקרה זה משולש נפוליאון הפנימי מנוון והופך לנקודה ומשולש נפוליאון החיצוני מתלכד עם המשולש המקורי.

ריצוף המישור

משפט נפוליאון מרמז על כך שניתן להשתמש בשלושה משולשים שווי-צלעות והמשולש הנוצר משלושת אורכי צלעותיהם כדי לרצף את המישור. בגלל שהמרחק בין מרכזי הכובד של כל זוג משולשים שווי צלעות נשאר זהה, הצפיפות של המשולשים נשארת קבועה כאשר מזיזים את הדיאגרמה במרחב.

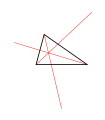
הריצוף נוצר באופן הבא:^[5]

מתחילים מהתרשים לעיל עם הנקודות $A, B, C, A^{'}, B^{'}, C^{'}$ . התרשים בנוי משלושה משולשים שווי צלעות ומשולש אחד כללי.
מזיזים את התרשים כולו בכפולות שלמות של שני וקטורי בסיס של סריג: $\vec{C^{'} C}$ ו- $\vec{B^{'} B}$ .
את ה"חורים" שנוצרים בריצוף ממלאים באמצעות סיבובים ב- $12 0^{\circ}$ של המשולש המקורי (שאינו שווה צלעות).

לריצוף זה שתי סימטריות בסיסיות:

סימטריה להזזה לפי שני וקטורי הבסיס של הסריג.
סימטריה לסיבוב ב- $12 0^{\circ}$ סביב מרכזו של אחד המשולשים שווי הצלעות.

נקודות חשובות

הדיאגרמה של משפט נפוליאון מאפשרת להגדיר מספר נקודות חשובות הנוגעות למשולש כלשהו.

נקודת פרמה

מציאת נקודת פרמה בשיטה הראשונה
מציאת נקודת פרמה בשיטה השנייה

בהינתן משולש כלשהו, נקודת פרמה של המשולש מוגדרת להיות הנקודה שממנה סכום המרחקים לשלושת קודקודי המשולש הוא המינימלי.

בהינתן הדיאגרמה של משפט נפוליאון עם משולשים שווי-צלעות הפונים החוצה מן המשולש, ניתן למצוא את נקודה זו באמצעות הדיאגרמה של משפט נפוליאון בשתי דרכים:^[6]

חוסמים כל משולש שווה-צלעות במעגל. ניתן להוכיח כי שלושת המעגלים הללו החתכים בנקודה יחידה, ושנקודה זו היא נקודת פרמה.
מותחים קטע מכל קודקוד של משולש שווה-צלעות שאינו נוגע במשולש הפנימי אל הקודקוד הנגדי לו במשולש הפנימי. ניתן להוכיח כי שלושת הקטעים הללו נחתכים בנקודה אחת, ושנקודה זו היא נקודת פרמה.

נקודת נפוליאון הראשונה והשנייה

נקודת נפוליאון הראשונה
נקודת נפוליאון השנייה

בהינתן משולש כלשהו, בונים עליו שלושה משולשים שווי-צלעות הפונים החוצה ממנו, כפי שמתואר במשפט נפוליאון. מכל מרכז של משולש שווה-צלעות מותחים קטע לקודקוד הנגדי לו במשולש המקורי. ניתן להוכיח כי שלושת הקטעים הללו נפגשים בנקודה אחת. נקודה זו נקראת נקודת נפוליאון הראשונה.^[7]

אם מבצעים את אותה הבנייה עם משולשים הפונים פנימה, מקבלים גם כן כי שלושת הקטעים הסופיים נחתכים בנקודה אחת, אך עבור משולש כללי נקודה זו שונה מנקודת נפוליאון הראשונה. נקודה זו נקראת נקודת נפוליאון השנייה.

שתי נקודות נפוליאון מהוות ההצמדה האיזוגונלית אחת של השנייה.

הכללות והרחבות

משפט פטר-דאגלס-ניומן

ערך מורחב – משפט פטר-דאגלס-ניומן

משפט פטר-דאגלס-ניומן (פד"ן בקיצור) עוסק בבניית משולשים שווי-שוקיים על גבי מצולע בעל $n$ קודקודים ( $n$ הוא מספר טבעי).^[8]

המשפט קובע שבהינתן מצולע עם $n$ קודקודים, בונים על גבי כל צלע שלו משולש שווה-שוקיים שזווית הראש שלו היא $\frac{2 k π}{n}$ עבור $1 \leq k \leq n - 2$ (הזווית נמדדת ברדיאנים) כלשהו. לוקחים את כל קודקודי הראש של המשולשים הללו ויוצרים מצולע חדש בעל $n$ קודקודים. חוזרים על התהליך $n - 2$ פעמים, כל פעם עם ערך אחר של $k$ , עד ש- $k$ קיבל את כל הערכים בין $1$ ל- $n - 2$ . המשפט קובע כי:

מרכזי הכובד של כל המצולעים שנוצרו בתהליך שווים למרכז הכובד של המצולע הראשון.

המצולע האחרון בשרשרת הוא מצולע משוכלל.

משפט נפוליאון הוא משפט פד"ן עבור $n = 3$ . יש לשים לב שבמשפט PDN בוחרים את קודקוד המשולש ולא את מרכז הכובד שלו. המשפטים שקולים עבור $n = 3$ מכיוון שזווית הראש של המשולשים במשפט פד"ן היא $12 0^{\circ}$ , ולכן היא מזהה את מרכז המשולש של המשולשים שווי-הצלעות, שבהם זווית הראש היא $6 0^{\circ}$ .

משפט נפוליאון עבור משולשים שאינם שווי-צלעות

במקרה של משפט נפוליאון עבור משולשים הפונים החוצה, ניתן להכליל את המשפט למשולשים שאינם שווי-צלעות.^[1]

במקרה זה, לוקחים שלושה משולשים דומים אשר שונים אחד מהשני על-ידי סיבוב ושינוי קנה-מידה בלבד (ללא שיקוף). ומצמידים אותם זה לזה כך שכל צלע דומה נבחרת פעם אחת ומרכיבים משולש פנימי כלשהו. לוקחים את מרכזי הכובד של שלושת המשולשים הדומים. אזי, משפט נפוליאון קובע שהמשולש הנוצר על-ידי שלושת מרכזי הכובד הללו דומה לשלושת המשולשים.

בדיאגרמה המצורפת, $△ A B^{'} C \sim △ B C A^{'} \sim △ C^{'} A B$ . מסמנים את הנקודות $L$ , $M$ ו- $N$ להיות מרכזי הכובד של המשולשים $△ C^{'} A B$ , $△ A B^{'} C$ ו- $△ B C A^{'}$ בהתאמה. אזי המשולש $△ L M N$ דומה לשלושת המשולשים החיצוניים. בפרט $△ L M N \sim △ A B^{'} C$ .

קישורים חיצוניים

מדיה וקבצים בנושא משפט נפוליאון בוויקישיתוף

משפט נפוליאון, באתר MathWorld (באנגלית)
משולש נפוליאון הפנימי, באתר MathWorld (באנגלית)
משולש נפוליאון החיצוני, באתר MathWorld (באנגלית)
גרסה אינטראקטיבית של משפט נפוליאון באתר של Wolfram Demonstrations.
Three pretty geometric theorems, proved by complex numbers, סרטון בערוץ "Jim Simons", באתר יוטיוב, Jan 12, 2022

ראו גם

הערות שוליים

^ ^1.0 ^1.1 Eric W. Weisstein, Napoleon's Theorem, mathworld.wolfram.com (באנגלית)
↑ Napoleon's Theorem, www.mathpages.com
↑ Napoleon's Theorem, Two Simple Proofs, www.cut-the-knot.org
↑ A second proof with complex numbers, www.cut-the-knot.org
↑ Napoleon's Theorem | NRICH, nrich.maths.org
↑ Napoleon's Theorem and the Fermat Point, sites.math.washington.edu
↑ Eric W. Weisstein, Napoleon Points, mathworld.wolfram.com (באנגלית)
↑ Eric W. Weisstein, Petr-Neumann-Douglas Theorem, mathworld.wolfram.com (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

משפט נפוליאון41921513Q637418

[:0-1] 1.0 ^1.1 Eric W. Weisstein, Napoleon's Theorem, mathworld.wolfram.com (באנגלית)

[2] Napoleon's Theorem, www.mathpages.com

[3] Napoleon's Theorem, Two Simple Proofs, www.cut-the-knot.org

[4] A second proof with complex numbers, www.cut-the-knot.org

[5] Napoleon's Theorem | NRICH, nrich.maths.org

[6] Napoleon's Theorem and the Fermat Point, sites.math.washington.edu

[7] Eric W. Weisstein, Napoleon Points, mathworld.wolfram.com (באנגלית)

[8] Eric W. Weisstein, Petr-Neumann-Douglas Theorem, mathworld.wolfram.com (באנגלית)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]