פתרון טיילור-ניומן-סדוב לגל הדף

גרפים של היחסים $\rho /\rho _{1},v/v_{1},T/T_{1}$ בתלות ב-$\xi$ (בתוך כדור ההדף, כלומר עבור $0\leq \xi \leq 1$) בפתרון עבור אוויר, לו $\gamma =7/5$. כאן $\rho ,v,T$ מייצגים את צפיפות, מהירות וטמפרטורת האוויר בהתאמה, ואילו $\rho _{1},v_{1},T_{1}$ מייצגים את ערכם על שפת כדור ההדף.

במכניקת הזורמים, פתרון טיילור-פון ניומן-סדוב לגל הדף מתאר את הפרמטרים (מהירות הזורם, לחצו ומהירות התפשטות גל ההדף) המאפיינים גלי הדף חזקים במיוחד כפתרון בעל דמיון עצמי. התיאור של גלי הדף חזקים על ידי פתרון כזה נתגלה באופן בלתי תלוי על ידי ג'. א. טיילור, ג'ון פון ניומן ולאוניד סדוב במהלך מלחמת העולם השנייה.

הנחת היסוד של הפתרון היא שמאחר שפיצוצים חזקים במיוחד (כמו אלו של פצצות גרעיניות) משחררים כמות עצומה של אנרגיה בשבריר שנייה, האנרגיה התרמית והלחצים של האוויר לפני חלוף חזית ההדף זניחים ביחס לאלו שבתוך כדור ההדף, כך שרק האנרגיה $E$ שמשתחררת בפיצוץ, צפיפות האוויר $\rho _{0}$ שמחוץ לכדור ההדף (הקובעת את האינרציה של האוויר – כמה חזית ההדף מאיצה אותו בקלות) והזמן $t$ קובעים את רדיוס כדור ההדף $R(t)$. מאנליזה ממדית עולה שתחת ההנחות הללו, רדיוס כדור ההדף הוא:

$R=\beta \left({\frac {Et^{2}}{\rho _{0}}}\right)^{1/5}.$

כאשר $\beta$ הוא קבוע חסר ממדים שנקבע מן הניתוח המתמטי העולה מתוך הנחת "הדמיון העצמי". הנחת הדמיון העצמי, שקשורה רעיונית להנחה הקודמת, היא שלפרמטרים המאפיינים את בעיית הזרימה בתוך כדור ההדף יש התנהגות מרחבית וזמנית הנתונה על ידי $f(\xi ,t)=F(t)G(\xi )$, כאשר $\xi =r/R(t)$ הוא פרמטר המייצג מרחק ממוקד הפיצוץ המנורמל על ידי רדיוס כדור ההדף – רדיוס זה מייצג את קנה המידה הטבעי של הבעיה הדינמית. במילים אחרות, הפילוג המרחבי של הפרמטרים המכניים (כגון הלחץ, מהירות הזורם וצפיפותו) בתוך כדור ההדף, כאשר קנה המידה של המרחק נקבע על ידי רדיוס הכדור, הוא קבוע בזמן.

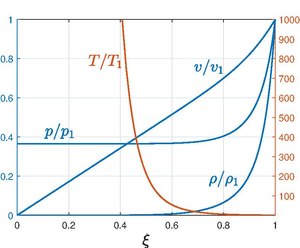
אם מתארים את היחס בין ערכם של פרמטרים אלו לערכם על חזית ההדף (כלומר לערכם כאשר $\xi =1$), כמו בתרשים משמאל, אז מתקבלת תלות ב-$\xi$ בלבד (ערכי פרמטרים אלו בחזית ההדף פוחתים עם הזמן, ולכן התלות בזמן נותרת בעינה). הנחה זאת נשארת תקפה כל עוד פרמטרים אלו גדולים בהרבה מאלו שמאפיינים את הזורם שמחוץ לכדור ההדף.

תיאור מתמטי

נתייחס לפיצוץ חזק המשחרר כמות גדולה של אנרגיה $E$ בנפח קטן במהלך פרק זמן קצר. זה יוביל ליצירת גל הלם כדורי המתפשט החוצה ממוקד הפיצוץ. פתרון בעל דמיון עצמי שואף לתאר את הזרימה כאשר גל ההלם התקדם מרחק שהוא גדול במיוחד בהשוואה לגודל חומר הנפץ שיצר אותו. במרחקים גדולים כאלה, המידע על גודל הפצצה ומשך שחרור האנרגיה יישכח; רק האנרגיה המשוחררת $E$ תהיה בעלת השפעה על איך גל ההלם יתפתח בזמן. לדרגת דיוק גבוהה מאוד, ניתן להניח שהפיצוץ אירע בנקודה (הראשית $r=0$) באופן מיידי בזמן $t=0$.

ההנחה היא שגל ההלם כה חזק שהלחץ $p_{1}$ מאחורי חזית גל ההלם גדול מאוד בהשוואה ללחץ (לחץ אטמוספירי) של האוויר בחזית גל ההלם (שאינו "יודע" עדיין על הפיצוץ), $p_{0}$, כך שניתן להזניחו בניתוח. אף על פי שהלחץ של האוויר הלא מופרע זניח, צפיפות האוויר הלא מופרע $\rho _{0}$ לא ניתנת להזנחה מכיוון שהקפיצה בצפיפות היא סופית וברת השוואה ל-$\rho _{0}$ כפועל יוצא ממשוואות רנקין-הוגוניו. קירוב זה שקול להנחה ש-$p_{0}=0$ ושמהירות הקול היא $c_{0}=0$, אך זאת תוך שמירה על הצפיפות שונה מאפס, כלומר $\rho _{0}\neq 0$.

הפרמטרים היחידים הקיימים ברשותנו הם לפיכך האנרגיה $E$ וצפיפות האוויר הלא-מופרעת $\rho _{0}$. התכונות של האוויר מאחורי חזית ההלם כגון $p_{1},\,\rho _{1}$ ניתנות לגזירה מאלו שבחזית גל ההלם. הצירוף חסר הממדים היחיד שניתן ליצור מ-$r,\,t,\,\rho _{0}$ ו-$E$ הוא:

$r\left({\frac {\rho _{0}}{Et^{2}}}\right)^{1/5}$.

פירוש הדבר הוא שההתפתחות בזמן של רדיוס גל ההלם $r=R(t)$ נתונה על ידי:

$R=\beta \left({\frac {Et^{2}}{\rho _{0}}}\right)^{1/5}.$

הניתוח המפורט שיובא מיד יגלה בסופו של דבר שהגורם המספרי $\beta$ קרוב למדי לאחד, ובכך מהווה דוגמה (בעבור הבעיה המסוימת הזאת) ליכולת החיזוי הכמותית של האנליזה הממדית. מהירות ההתקדמות של גל ההלם היא

$D={\frac {\mathrm {d} R}{\mathrm {d} t}}={\frac {2R}{5t}}={\frac {2\beta }{5}}\left({\frac {E}{\rho _{0}t^{3}}}\right)^{1/5}$

תחת הקירוב שמתואר לעיל, משוואות רנקין-הוגוניו קובעות את מהירות הזרימה של האוויר מיד מאחורי חזית ההלם $v_{1}$ ואת לחצו $p_{1}$ וצפיפותו $\rho _{1}$, תחת מודל הגז האידיאלי, כדלהלן

$v_{1}={\frac {2}{\gamma +1}}D,\quad p_{1}={\frac {2}{\gamma +1}}\rho _{0}D^{2},\quad \rho _{1}=\rho _{0}{\frac {\gamma +1}{\gamma -1}}$

כאשר $\gamma$ הוא יחס קיבולי החום. מכיוון ש-$\rho _{0}$ הוא קבוע, הצפיפות מיד מאחורי חזית ההלם אינה משתנה בזמן (אם נציב, עבור אוויר, $\gamma =7/5$ נקבל ש-$\rho _{1}/\rho _{0}=6$), בעוד ש-$v_{1}$ ו-$p_{1}$ יורדים כמו $t^{-3/5}$ ו-$t^{-6/5}$, בהתאמה.

פתרון הדמיון העצמי

תנועת הגז מאחורי גל ההלם נשלטת על ידי משוואות אוילר. בעבור גז פוליטרופי אידיאלי עם סימטריה כדורית, המשוואות עבור משתני הזורם כמו המהירות הרדיאלית $v(r,t)$, הצפיפות $\rho (r,t)$ והלחץ $p(r,t)$ נתונות על ידי

${\begin{aligned}{\frac {\partial v}{\partial t}}+v{\frac {\partial v}{\partial r}}&=-{\frac {1}{\rho }}{\frac {\partial p}{\partial r}},\\{\frac {\partial \rho }{\partial t}}+{\frac {\partial (\rho v)}{\partial r}}&=-{\frac {2\rho v}{r}},\\\left({\frac {\partial }{\partial t}}+v{\frac {\partial }{\partial r}}\right)\ln {\frac {p}{\rho ^{\gamma }}}&=0.\end{aligned}}$

ב-$r=R(t)$, הפתרונות צריכים לקבל את הערכים שהוסקו ממשוואות רנקין-הוגוניו בחלק הקודם.

את הלחץ המשתנה ניתן להחליף על ידי מהירות הקול המקומית $c(r,t)$, שכן ניתן לקבל אותו מהמשוואה $c^{2}=\gamma p/\rho$. הצגת הגדלים חסרי הממדים הבאים

$\xi ={\frac {r}{R(t)}},\quad V(\xi )={\frac {5tv}{2r}},\quad G(\xi )={\frac {\rho }{\rho _{0}}},\quad Z(\xi )={\frac {25t^{2}c^{2}}{4r^{2}}}$.

(המתייחסים לסקלות האורך, מהירות הזורם, צפיפותו ולחצו, בהתאמה) כאשר התנאים בחזית ההלם, כלומר כש-$\xi =1$, הם

$V(1)={\frac {2}{\gamma +1}},\quad G(1)={\frac {\gamma +1}{\gamma -1}},\quad Z(1)={\frac {2\gamma (\gamma -1)}{(\gamma +1)^{2}}}.$

מאפשרת לממש מתמטית את הנחת הדמיון העצמי, שכן הצבתם במשוואות השולטות בדינמיקה מאפשרת להמיר את הבעיה לשלוש משוואות דיפרנציאליות רגילות עבור כל אחד מהגדלים $V,G,Z$ כפונקציה של $\xi$. פתירת המשוואות הדיפרנציאליות הללו אנליטית היא קשה ומפרכת, כפי שהראו סדוב ב-1946 ופון ניומן ב-1947. ג'. א. טיילור ביצע אינטגרציה נומרית של המשוואות הללו כדי להשיג את התוצאות הרצויות.

את הקשר בין $Z$ ו-$V$ ניתן לגזור ישירות משימור אנרגיה. מכיוון שהאנרגיה המקושרת לגז הלא מופרע מוזנחת בכך שמניחים $p_{0}=0$, האנרגיה הכוללת של הגז בתוך כדור ההדף חייבת להיות שווה ל-$E$. אודות לדמיון העצמי, לא רק האנרגיה הכוללת בתוך הכדור בעל רדיוס $\xi =1$ היא קבועה, אלא גם שהאנרגיה הכוללת בתוך הכדור בעל כל רדיוס שהוא $\xi <1$ היא קבועה (בצורה ממדית, פירוש הדבר שהאנרגיה הכוללת בתוך כדור בעל רדיוס $r$ המתפשט החוצה במהירות $v_{n}=2r/5t$ חייבת להיות קבועה). כמות האנרגיה שעוזבת כדור ברדיוס $r$ בפרק זמן קצרצר $dt$ אודות למהירות הגז $v$ והאנרגיה התרמית שלו היא $4\pi r^{2}\rho v(h+v^{2}/2)\mathrm {d} t$ כאשר $h$ היא האנתלפיה הסגולית של הגז. בפרק זמן זה, רדיוס הכדור גדל במהירות $v_{n}$ והאנרגיה של הגז בנפח המתווסף הזה היא $4\pi r^{2}\rho v_{n}(e+v^{2}/2)\mathrm {d} t$ כאשר $e$ היא האנרגיה הסגולית של הגז. השוואת הביטויים הללו והצבת הקשרים $e=c^{2}/\gamma (\gamma -1)$ ו-$h=c^{2}/(\gamma -1)$ התקפים לגז אידיאלי מובילה ל-

$Z={\frac {\gamma (\gamma -1)(1-V)V^{2}}{2(\gamma V-1)}}.$

הצגת הגדלים חסרי הממדים מאפשרת לזהות את אופרטור הגזירה המרחבי ${\frac {\partial }{\partial r}}$ עם ${\frac {\xi }{r}}{\frac {\partial }{\partial \xi }}$ ואת אופרטור הגזירה בזמן ${\frac {\partial }{\partial t}}$ עם ${\frac {2\xi }{5t}}{\frac {\partial }{\partial \xi }}$, ולפיכך משוואת הרציפות ומשוואת האנרגיה (השנייה והשלישית במשוואות אוילר) המתקבלות הן

${\begin{aligned}{\frac {\mathrm {d} V}{\mathrm {d} \ln \xi }}-(1-V){\frac {\mathrm {d} \ln G}{\mathrm {d} \ln \xi }}&=-3V\\{\frac {\mathrm {d} \ln Z}{\mathrm {d} \ln \xi }}-(\gamma -1){\frac {\mathrm {d} \ln G}{\mathrm {d} \ln \xi }}&=-{\frac {5-2V}{1-V}}.\end{aligned}}$

ביטוי של $\mathrm {d} V/\mathrm {d} \ln \xi$ ו-$\mathrm {d} \ln G/\mathrm {d} V$ כפונקציה של $V$ בלבד באמצעות הקשר שהובא מקודם ואינטגרציה פעם אחת מניב את הפתרון בצורה בלתי מפורשת

${\begin{aligned}\xi ^{5}&=\left[{\frac {1}{2}}(\gamma +1)V\right]^{-2}\left\{{\frac {\gamma +1}{7-\gamma }}[5-(3\gamma -1)V]\right\}^{\nu _{1}}\left[{\frac {\gamma +1}{\gamma -1}}(\gamma V-1)\right]^{\nu _{2}},\\G&={\frac {\gamma +1}{\gamma -1}}\left[{\frac {\gamma +1}{\gamma -1}}(\gamma V-1)\right]^{\nu _{3}}\left\{{\frac {\gamma +1}{7-\gamma }}[5-(3\gamma -1)V\right\}^{\nu _{4}}\left[{\frac {\gamma +1}{\gamma -1}}(1-V)\right]^{\nu _{5}}\end{aligned}}$

כאשר

$\nu _{1}=-{\frac {13\gamma ^{2}-7\gamma +12}{(3\gamma -1)(2\gamma +1)}},\quad \nu _{2}={\frac {5(\gamma -1)}{2\gamma +1}},\quad \nu _{3}={\frac {3}{2\gamma +1}},\quad \nu _{4}=-{\frac {\nu _{1}}{2-\gamma }},\quad \nu _{5}=-{\frac {2}{2-\gamma }}.$

הקבוע $\beta$ שקובע את מיקום חזית ההלם ניתן לקביעה משימור אנרגיה

$E=\int _{0}^{R}\rho [v^{2}/2+c^{2}/\gamma (\gamma -1)]4\pi r^{2}\mathrm {d} r$

וכך מקבלים

$\beta ^{5}{\frac {16\pi }{25}}\int _{0}^{1}G[V^{2}/2+Z/\gamma (\gamma -1)]\xi ^{4}\mathrm {d} \xi =1.$

בעבור אוויר, $\gamma =7/5$ ו-$\beta =1.033$.

התנהגות אסימפטוטית קרוב למוקד הפיצוץ

ההתנהגות האסימפטוטית של האזור הקרוב למוקד הפיצוץ ניתנת לחקירה באמצעות לקיחת הגבול $\xi \rightarrow 0$. מן הגרף לעיל, ניתן לראות שהצפיפות דועכת לאפס מהר מאוד מאחורי גל ההלם. המסה הכוללת של הגז אשר הייתה בתחילה מפולגת באופן אחיד בתוך כדור ברדיוס $R$ מוכלת כעת בשכבה דקה יחסית מאחורי גל ההלם, שכן מסת הגז מונעת החוצה באמצעות התאוצה העצומה שגורם גל ההלם. לפיכך, רוב האזור שבתוך כדור ההדף הוא למעשה מרוקן. יחס הלחצים גם דועך מהר, אבל מתכנס לערך קבוע שונה מאפס $p_{c}$ בסביבת מוקד הפיצוץ. יחס הטמפרטורות נובע ממשוואת הגז האידיאלי; מכיוון שהצפיפות שואפת לאפס ויחס הלחצים קבוע, יחס הטמפרטורות שואף לאינסוף. ההתנהגות הגבולית של הצפיפות ניתנת על ידי

${\frac {\rho }{\rho _{1}}}\sim \xi ^{3/(\gamma -1)},\quad {\frac {p}{p_{1}}}\rightarrow p_{c},\quad {\frac {T}{T_{1}}}\sim \xi ^{-3/(\gamma -1)}\quad {\text{as}}\quad \xi \rightarrow 0.$

הצפיפות $\rho _{1}$ היא בלתי תלויה בזמן, בעוד ש-$p_{1}\sim t^{-6/5}$, מה שאומר שהלחץ במרכז תלוי בזמן. זה נעשה ברור אף יותר אם הביטויים לעיל נכתבים מחדש באופן הבא,

$\rho \sim r^{3/(\gamma -1)}t^{-6/5(\gamma -1)},\quad p\rightarrow p_{c}t^{-6/5},\quad T\sim r^{-3/(\gamma -1)}t^{(6/5)(2-\gamma )/(\gamma -1)}\quad {\text{as}}\quad r\rightarrow 0.$

ליחס המהירויות התנהגות ליניארית באזור המרכזי,

${\frac {v}{v_{1}}}\sim \xi \quad {\text{as}}\quad \xi \rightarrow 0$

בעוד שההתנהגות של המהירות עצמה נתונה על ידי

$v\sim rt^{1/5}\quad {\text{as}}\quad r\rightarrow 0.$

השלב הסופי של גל ההדף

כשגל ההלם מתפתח בזמן, עוצמתו פוחתת. פתרון הדמיון העצמי שתואר לעיל אינו תקף כאשר $p_{1}$ הופך בר-השוואה ל-$p_{0}$ (ביותר דיוק, כאשר $p_{1}\sim [(\gamma +1)/(\gamma -1)]p_{0}$). בשלב מאוחר זה של ההתפתחות, $p_{0}$ (ובעקבות כך גם $c_{0}$) אינו ניתן להזנחה. פירוש הדבר שההתפתחות בזמן אינה בעלת דמיון עצמי, שכן מרגע שהלחץ האטמוספירי $p_{0}$ הופך לחשוב אז ניתן להרכיב בעזרתו סקלת מרחק $(E/p_{0})^{1/3}$ וסקלת זמן $(E/p_{0})^{1/3}/c_{0}$ כדי לתאר את הבעיה. במקרה כזה, אין מנוס משימוש באינטגרציה נומרית, כפי שעשו H. Goldstine, ג'ון פון ניומן ואחרים.

פיצוץ קו גלילי

הבעיה האנלוגית בגאומטריה גלילית עוסקת בגל הדף בעל סימטריה גלילית, כמו זה הנוצר במעבר ברק, והיא ניתנת לפתרון אנליטי. בעיה זו נפתרה באופן בלתי תלוי על ידי לאוניד סדוב ו-S. C. Lin. עבור גל הדף גלילי, הצירוף חסר הממדים המערב את המרחק מהציר $r$, הזמן $t$, האנרגיה הכוללת המשוחררת ליחידת אורך של הציר $E$ וצפיפות התווך המקיף $\rho _{0}$ היא

$r\left({\frac {\rho _{0}}{Et^{2}}}\right)^{1/4}.$

ראו גם

• גל הדף
• גל הלם

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

פתרון טיילור-ניומן-סדוב לגל הדף41264406Q104868831