שכבת גבול סטוקס
בהידרודינמיקה, שכבת גבול סטוקס, או שכבת גבול תונדת, מתייחסת לשכבת גבול הקרובה לקיר מוצק בזרימה תונדת של זורם צמיג, או למקרה הדומה של משטח תונד בזורם צמיג במנוחה, עם כיוון התנודה במקביל למשטח. במקרה של זרימה למינרית עם מספרי ריינולדס נמוכים על קיר מוצק חלק, ג'ורג' גבריאל סטוקס – ששכבת הגבול נקראת על שמו - פיתח פתרון אנליטי, אחד מהפתרונות המדויקים של משוואות נאוויה-סטוקס.[1][2] גם בזרימה טורבולנטית מושג זה קרוי "שכבת גבול סטוקס", אך יש להסתמך על ניסויים, הדמיות מספריות או בשיטות קירוב על מנת לקבל מידע שימושי על הזרימה.
עובי שכבת הגבול התונדת נקרא עובי שכבת גבול סטוקס.
תנודות ערבוליות קרובות לגבול
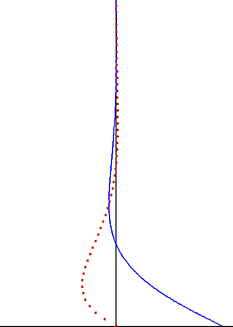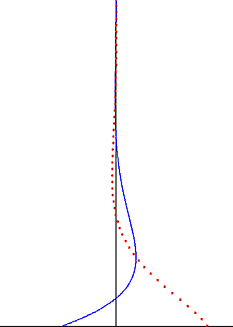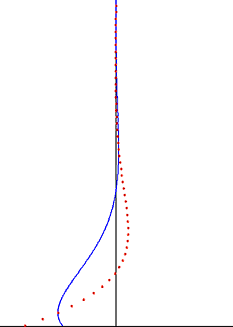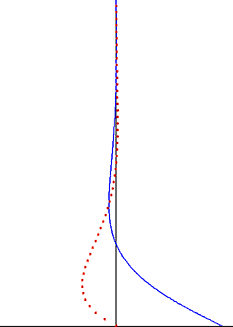
מבט נוסף מפתרון סטוקס עבור זרימת סטוקס תונדת היא שהתנודות הערבוליות מתוחמות כשכבת גבול דקה ולחה הדועכת באופן אקספוננציאלי כאשר מתרחקים מהקיר[3]. התבוננות זו תקפה גם עבור מקרה של שכבת גבול טורבולנטית. מחוץ לשכבת גבול סטוקס - אשר לעיתים זו כמות גדולה של נפח הזורם - התנודות הערבוליות זניחות. בקירוב טוב, תנודות מהירות הזרימה הן אי-רוטציוניות מחוץ לשכבת הגבול, וניתן להחיל את תיאורית הזרימה הפוטנציאלית לתנועה התונדת. כך ניתן לפשט משמעותית את פתרון בעיות זרימה מסוג זה, ולהחילן על האזורים האי רוטציוניים בגלי קול וגלי מים.
שכבת גבול סטוקס עבור זרימה למינרית קרובה לקיר
נניח כי הזרימה התונדת תהיה חד-כיוונית ומקבילה לקיר. רכיב המהירות השונה מאפס נקרא u (ביחידות של מטר/שנייה) והוא נע בכיוון x המקביל לכיוון התנודה. יתר על כן, כיוון שהזורם אי-דחיס, רכיב המהירות u הוא רק פונקציה של הזמן t (בשניות) והמרחק מהקיר z (מטר). מספר ריינולדס קטן מספיק עבור זרימה למינרית. אז משוואות נאוויה-סטוקס תהיה:[4]
כאשר:
- ρ - צפיפות הנוזל (kg/m3), הוא קבוע.
- p - לחץ הנוזל (פסקל).
- ν - צמיגות קינמטית של הנוזל (m2/s), היא קבועה.
ו
- u - מהירות של הנוזל לאורך המשטח (m/s)
- x - מיקום לאורך המשטח (מ')
- z - המרחק מהמשטח (m)
- t - זמן (s)
כיוון שהמהירות u אינה פונקציה של המיקום x, גרדיאנט הלחץ p/∂x∂ גם הוא אינו תלוי ב-x (אבל הלחץ p משתנה באופן ליניארי כתלות ב-x). יתר על כן, רכיב המהירות הניצב לקיר במשוואות נאוויה סטוקס שואף ל
0=p/∂z∂ לכן גם הלחץ p וגם גרדיאנט הלחץ p/∂x∂ אינם תלויים במרחק z. לסיכום, גרדיאנט הלחץ p/∂x∂ יכול להיות רק פונקציה של הזמן t.[4]
הרכיב שאינו אפס בווקטור ערבוליות בכיוון המאונך ל-x ו-z, נקרא (ω (s-1 ושווה ל:[3]
נגזור לפי z מהמשוואה לעיל, ω נתון[3]
בדינמיקה של ערבוליות, הלחץ נופל במשוואת הערבוליות.[5]
תנודת לוח מישורי קשיח
תנועה הרמונית של לוח מישורי קשיח - הנע במקביל למישור - כתוצאה מכך הזורם הקרוב למשטח ייגרר יחד עם המשטח, בשל מאמץ הגזירה. נניח כי התנועה של הלוחית
כאשר:
הלוחית, הממוקמת ב z = 0, מאלצת את הזורם הצמיג בסמוך אליה לנוע באותה המהירות (u1( z, t וכתוצאה מתנאי אי-החלקה נקבל ש:
רחוק מהלוחית, עבור ∞→z , המהירות u1 שואפת לאפס. כתוצאה מכך, גרדיאנט הלחץ p/∂x∂ הוא אפס באינסוף, כיוון שהוא פונקציה רק של הזמן. t ולא של z, אזי חייב להיות אפס בכל מקום:[6]
משוואה מהצורה הנ"ל נקראת משוואה חד-ממדית משוואת חום או משוואת הדיפוזיה.
| פרטים על נגזרת הפתרון |
|---|
ניתן לפתור משוואה זו עבור תנועה הרמונית תוך כדי שימוש במספרים מרוכבים והפרדת משתנים:[7]
כאשר i2 = −1 ו - {•}ℜ הוא החלק הממשי של הערך בסוגריים
עבור תנאי השפה הבאים: הפתרון (F(z יהיה: |
כתוצאה מכך, הפתרון עבור מהירות הזרימה הוא[7]
כאן, κ הוא סוג של מספר הגל בכיוון z, הקשור עם האורך
וזה נקרא עובי שכבת גבול סטוקס. במרחק דלתא מהפלטה\לוח. המהירות הופחתה ל- e^2π = 0.002 פעמים הערך U0 על פני הפלטה. בנוסף, כפי שניתן לראות משינויי הפאזה Ω t − κ z בפתרון u1, תנודות המהירות נעות מהקיר כגל מרוסן בעל אורך גל דלתא ומהירות פאזה Ω / κ.
הערבוליות ω1 שווה ל -
u1 קטן באופן אקספוננציאלי כאשר מתרחקים ממישור הלוחית.
זרימה בשל תנודת גרדיאנט הלחץ קרוב ללוח מישורי קשיח

במקרה של תנודת נדנוד רחוק, שדה זרימה, עם צלחת מוחזק במנוחה, יכול בקלות להיות בנוי הקודמת פתרון נדנוד הצלחת על ידי שימוש ליניארי סופרפוזיציה של פתרונות. לשקול מדים מהירות תנודה ∞u:
אשר מתאר את משוואות הזרימה של שכבת גבול סטוקס
חיסור הפתרון (u1(z, t מ (u∞(z, t נותן פתרון לזרימה תונדת הקרובה לקיר במנוחה:[3]
שהיא 0 על הקיר, בהתאם לתנאי אי ההחלקה. רחוק יותר מהקיר, המהירות u2 תונדת עם משרעת U0 עבור z → ∞. מצב זה מתקבל לעיתים קרובות בגלי קול ליד פלטה קשיחה, או בתנועת המים בקרקעית הים בהשפעת גלי מים.
הערבוליות במקרה של זרימה תונדת ליד קיר נייח, שווה לערבוליות של פלטה תונדת אך עם סימן הפוך: ω2 = − ω1.
ראו גם
- כוח באסט
- זרימת סטוקס
הערות שוליים
- ↑ Wang, C. Y., "Exact solutions of the steady-state Navier-Stokes equations". Annual Review of Fluid Mechanics. 23: 159–177., http://www.annualreviews.org/doi/10.1146/annurev.fl.23.010191.001111, 1991
- ↑ Landau & Lifshitz (1987), pp. 83–85.
- ^ 3.0 3.1 3.2 3.3 Phillips (1977), p. 46.
- ^ 4.0 4.1 Batchelor (1967), p. 179
- ↑ Since the vorticity equation is obtained by taking the curl of the Navier–Stokes equations, and the curl of the pressure gradient equals zero, see vector calculus identities
- ↑ Batchelor (1967), p. 190
- ^ 7.0 7.1 Batchelor (1967), p. 192
שכבת גבול סטוקס40611628Q7618545


