Theorema Elegantissimum

המשפט בגאומטריה היפרבולית; משולש על פני משטח בצורת אוכף. עקמומיות המשטח שלילית ולכן סכום הזוויות במשולש קטן מ-180°

המשפט עבור משטח כדורי. עקמומיות המשטח חיובית ולכן סכום הזוויות במשולש גדול מ-180°

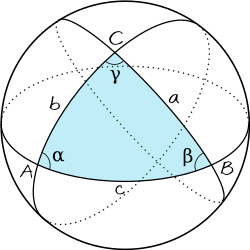
Theorema Elegantissimum (בלטינית: המשפט האלגנטי) הוא משפט קלאסי בגאומטריה של משטחים, הנוגע לסכום הזוויות במשולש על פני משטח עקום. את המשפט, שהוא מקרה פרטי של משפט גאוס-בונה, הוכיח קרל פרידריך גאוס. המשפט קובע כי המגרעת הזוויתית של המשולש, כלומר ההפרש בין סכום זוויותיו ל-180°, שווה לאינטגרל על עקמומיות (עקמומיות גאוס) המשטח בתחום המשולש.

ניסוח מדויק

גאוס הוכיח שאם $T$ הוא משולש גאודזי, אזי סכום זוויותיו הוא $\pi +\underset{T}{\iint }KdA$ , כאשר הגודל $\underset{T}{\iint }KdA$ הוא העקמומיות הכוללת (Total Curvature) של המשטח בתחום המשולש $T$ . באופן כללי יותר, אם $P$ הוא מצולע גאודטי בעל $n$ צלעות, אזי סכום זוויותיו הוא $(n-2)\pi +\underset{P}{\iint }KdA$ .

מסקנות מן המשפט והכללות שלו

מסקנות:

• כמסקנה מן המשפט נובע שסכום הזוויות המרבי של משולש על פני כדור הוא 540°.

הכללות:

• משפט גאוס-בונה מכליל את המשפט למקרה שצלעותיו של המשולש אינן קווים גאודזיים של המשטח. המשפט משלב בין רעיונות מגאומטריה דיפרנציאלית כמו עקמומיות גאוס ועקמומיות גאודזית לרעיונות מטופולוגיה כמו מאפיין אוילר לכדי קשר מתמטי עמוק ויוצא מן הכלל. משפט זה הוא הפרוטוטיפ של משפטי האינדקס שהתפתחו במאה ה-20.

מקורות

• Dictionary of Analysis, Calculus and Differential Equations, Douglas N. Clark.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0