הבינום של ניוטון

בערך זה
נעשה שימוש
בסימנים מוסכמים
מתחום המתמטיקה.
להבהרת הסימנים
ראו סימון מתמטי.

במתמטיקה, הבינום של ניוטון היא נוסחה לפיתוח חזקות של סכום של שני איברים.

על-פי נוסחת הבינום, ניתן לפתח את החזקה $(x + y)^{n}$ לסכום הכולל ביטויים מהצורה $a x^{b} y^{c}$ , כאשר החזקות $b, c$ הן מספרים שלמים לא שליליים המקיימים $b + c = n$ , והמקדם $a$ של כל ביטוי הוא מספר שלם חיובי ספציפי התלוי ב- $b, c$ . לדוגמא:

(x + y)^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4}

המקדם $a$ בביטוי $a x^{b} y^{c}$ מכונה מקדם בינומי $(\binom{n}{b})$ או $(\binom{n}{c})$ (לשניהם יש אותו הערך).

נוסחת הבינום עבור חזקה שלמה

על-פי הבינום של ניוטון ניתן לפתח כל חזקה של $x + y$ לסכום בצורה הזו:

(x + y)^{n} = (\binom{n}{0}) x^{n} y^{0} + (\binom{n}{1}) x^{n - 1} y^{1} + (\binom{n}{2}) x^{n - 2} y^{2} + \dots + (\binom{n}{n - 1}) x^{1} y^{n - 1} + (\binom{n}{n}) x^{0} y^{n}

נוח להגדיר חזקת אפס כשווה ל-1 תמיד, משום ש: $a^{0} = a^{n - n} = \frac{a^{n}}{a^{n}} = 1$ .

בנוסף, המספר 1 הוא איבר יחידה ביחס לכפל כך ש:

1 \cdot x = x \cdot 1 = x

כלומר, כל מספר כפול 1 שווה למספר עצמו ולכן גם מכפלה במספר כלשהו בחזקת 0 שווה למספר עצמו, כך ש:

a^{0} \cdot x = x \cdot a^{0} = x

בהתאם לכך, נהוג לעיתים לכתוב בנוסחת הבינום גם $(\binom{n}{0}) x^{n} + \dots$ במקום $(\binom{n}{0}) x^{n} y^{0} + \dots$ , תוך השמטת הביטוי $y^{0}$ - שהרי כל מספר שיוכפל בו יהיה שווה לעצמו.

מכאן שניתן לכתוב את נוסחת הבינום גם בדרך זו:

(x + y)^{n} = (\binom{n}{0}) x^{n} + (\binom{n}{1}) x^{n - 1} y^{1} + (\binom{n}{2}) x^{n - 2} y^{2} + \dots + (\binom{n}{n - 1}) x^{1} y^{n - 1} + (\binom{n}{n}) y^{n}

בעזרת סימן הסכום סיגמא גדולה (Σ), ניתן לסמן את נוסחת הבינום בדרך מקוצרת. כך שאם $n$ מספר שלם, אז לכל $x, y$ מתקיים:

$(x + y)^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) x^{n - k} y^{k} = \sum_{k = 0}^{n} (\binom{n}{k}) x^{k} y^{n - k}$

כאשר הביטוי האחרון נובע מקודמו, עקב הסימטריה בין $x, y$ בביטוי הראשון.

מקדם הבינום

ערך מורחב – מקדמי הבינום

המקדמים של $x^{n - k} y^{k}$ המופיעים בביטויים של נוסחת הבינום הם מספרים שלמים חיוביים המכונה מקדמי הבינום.

לכל $0 \leq k \leq n$ נגדיר:

$(\binom{n}{k}) = \frac{n!}{k! (n - k)!}$

הסימן "!" מציין עצרת, שהיא מכפלת כל המספרים הטבעיים מ-1 ועד למספר נתון.

כלומר: $n! = 1 \times 2 \times \dots \times n$
ובאופן דומה: $k! = 1 \times 2 \times \dots \times k, (n - k)! = 1 \times 2 \times \dots \times (n - k)$
כמו כן, $0! = 1$

ניתן לכתוב את הנוסחה של מקדם הבינום גם כך:

(\binom{n}{k}) = \frac{n (n - 1) (n - 2) \dots (n - (k - 1))}{k!} = \frac{n (n - 1) \dots (n - k + 1)}{k (k - 1) \dots 1} = \prod_{m = 1}^{k} \frac{n - m + 1}{m} = \prod_{m = 0}^{k - 1} \frac{n - m}{k - m}

למרות שנוסחת הבינום מורכבת משבר הערכים של המקדמים הבינומיים הם תמיד מספרים שלמים.

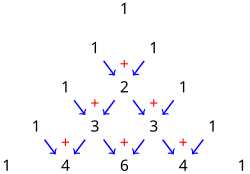
ניתן לסדר את המקדמים הבינומיים כך שירכיבו יחדיו את משולש פסקל. זהו סידור של מספרים בצורת משולש, שקדקודו העליון מכיל את המספר 1 וכל מספר במשולש מהווה את סכום שני המספרים שנמצאים מעליו, כאשר המספרים שנמצאים על שוקי המשולש הם כולם 1.


ניתן להרכיב את משולש פסקל ממקדמי הבינום של ניוטון, כך שכל מספר במשולש מהווה את סכום שני המספרים שנמצאים מעליו.

למקדמי הבינום שימושים רבים בקומבינטוריקה והסתברות. זאת משום שהמקדם הבינומי $(\binom{n}{k})$ הוא מספר תתי־הקבוצות בגודל $k$ שניתן לבחור מתוך קבוצה בגודל $n$ . כלומר, זהו מספר האפשרויות לבחור $k$ אברים מתוך $n$ , ללא חזרות וללא חשיבות לסדר.

דוגמאות לשימוש בנוסחת הבינום

המקרים הראשונים של הנוסחה הם:

$(x + y)^{1} = x + y$
$(x + y)^{2} = x^{2} + 2 x y + y^{2}$
$(x + y)^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}$
$(x + y)^{4} = x^{4} + 4 x^{3} y + 6 x^{2} y^{2} + 4 x y^{3} + y^{4}$
$(x + y)^{5} = x^{5} + 5 x^{4} y + 10 x^{3} y^{2} + 10 x^{2} y^{3} + 5 x y^{4} + y^{5}$
$(x + y)^{6} = x^{6} + 6 x^{5} y + 15 x^{4} y^{2} + 20 x^{3} y^{3} + 15 x^{2} y^{4} + 6 x y^{5} + y^{6}$
$(x + y)^{7} = x^{7} + 7 x^{6} y + 21 x^{5} y^{2} + 35 x^{4} y^{3} + 35 x^{3} y^{4} + 21 x^{2} y^{5} + 7 x y^{6} + y^{7}$

הוכחות

הוכחה קומבינטורית

ראשית, נשים לב כי $(x + y)^{n} = (x + y) (x + y) \dots (x + y)$ . באגף ימין מופיעים $n$ ביטויים המוכפלים זה בזה. התוצאה היא סכום של כל המכפלות האפשריות שבהן נבחר אבר אחד מכל אחד מהסוגריים. למשל,

(x + y)^{2} = (x + y) (x + y) = x x + x y + y x + y y = x^{2} + 2 x y + y^{2}

כשבוחרים את האבר $x$ מהסוגריים הראשונים ו- $x$ מהשניים, $x$ מהסוגריים הראשונים ו- $y$ מהשניים, וכן הלאה.

מכיון שהסדר בהכפלת המשתנים אינו חשוב, הביטוי $x^{k} y^{m}$ מופיע בכל פעם שבוחרים $k$ פעמים ב- $x$ ו- $m$ פעמים ב- $y$ , ובהכרח $k + m = n$ . לקביעת $k$ המקומות מתוך $n$ שבהם נבחר דווקא $x$ יש $(\binom{n}{k})$ אפשרויות, ולכן זהו המקדם של $x^{k} y^{n - k}$ .

הוכחה באינדוקציה

צריך להוכיח: $(a + b)^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) a^{k} b^{n - k}$

בדיקה עבור $n = 1$ (ניתן לבדוק גם החל מ- $n = 0$ ):

$(a + b)^{1} = \sum_{k = 0}^{1} (\binom{1}{k}) a^{k} b^{1 - k} = (\binom{1}{0}) a^{0} b^{1} + (\binom{1}{1}) a^{1} b^{0} = b + a$

הנחת האינדוקציה: נניח נכונות עבור $n = m$ :

$(a + b)^{m} = \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k}$

ונוכיח נכונות עבור $n = m + 1$ :

$(a + b)^{m + 1} = \sum_{k = 0}^{m + 1} (\binom{m + 1}{k}) a^{k} b^{m + 1 - k}$

הוכחה

$(a + b)^{m + 1} = (a + b)^{m} (a + b)$ . נשתמש בהנחת האינדוקציה ונחליף את $(a + b)^{m}$ בביטוי $\sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k}$ . אזי

\begin{aligned} (a + b) \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k} & = a \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k} + b \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k} \\ = \sum_{k = 0}^{m} (\binom{m}{k}) a^{k + 1} b^{m - k} + \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k + 1} \\ = \sum_{k = 1}^{m + 1} (\binom{m}{k - 1}) a^{k} b^{m - k + 1} + \sum_{k = 0}^{m} (\binom{m}{k}) a^{k} b^{m - k + 1} \\ = (\binom{m}{m}) a^{m + 1} b^{0} + \sum_{k = 1}^{m} (\binom{m}{k - 1}) a^{k} b^{m - k + 1} + (\binom{m}{0}) a^{0} b^{m + 1} + \sum_{k = 1}^{m} (\binom{m}{k}) a^{k} b^{m - k + 1} \\ = a^{m + 1} + b^{m + 1} + \sum_{k = 1}^{m} ((\binom{m}{k - 1}) + (\binom{m}{k})) a^{k} b^{m - k + 1} \\ = a^{m + 1} + b^{m + 1} + \sum_{k = 1}^{m} (\binom{m + 1}{k}) a^{k} b^{m - k + 1} = \sum_{k = 0}^{m + 1} (\binom{m + 1}{k}) a^{k} b^{m - k + 1} \end{aligned}

כאשר השתמשנו בזהות $(\binom{m}{k - 1}) + (\binom{m}{k}) = (\binom{m + 1}{k})$ ממשולש פסקל. בכך הושלמה הוכחת צעד האינדוקציה.

$◼$

גרסאות של נוסחת הבינום

גרסה פשוטה של נוסחת הבינום מתקבלת על ידי הצבת המספר 1 במשתנה $y$ , כך שהיא תכיל רק משתנה יחיד.

בגרסה זו הנוסחה תראה כך:

(1 + x)^{n} = (\binom{n}{0}) x^{0} + (\binom{n}{1}) x^{1} + (\binom{n}{2}) x^{2} + \dots + (\binom{n}{n - 1}) x^{n - 1} + (\binom{n}{n}) x^{n}

או כך:

(1 + x)^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) x^{k}

היסטוריה והתפתחות

הנוסחה עבור חזקה שלמה היתה ידועה זמן רב לפני ניוטון. בלז פסקל חקר אותה במהלך המאה ה-17, אך הייתה ידועה גם למתמטיקאים שקדמו לו, ובהם הסיני יאנג חווי בן המאה ה-13, הפרסי עומר ח'יאם בן המאה ה-11, וההודי פינגלה בן המאה ה-3. את הגרסה הכללית, שבה החזקה יכולה להיות מספר כלשהו, פיתח ניוטון בעזרת השיטות של החשבון האינפיניטסימלי שהמציא.

המקרה הכללי

ניוטון הראה שלכל $r$ ממשי מתקיים

$(1 + x)^{r} = \sum_{m = 0}^{\infty} (\binom{r}{m}) x^{m}$ כאשר $(\binom{r}{m}) = \frac{r (r - 1) \dots (r - m + 1)}{m!}$

זהו טור אינסופי, המתכנס אל הערך הנכון לכל $x$ , ותקף גם כאשר $r$ מרוכב. אם $r$ שלם, רק $r + 1$ המקדמים הראשונים שונים מ-0, והטור הוא למעשה סכום סופי. את המקרה הכללי אפשר לחשב לפי $(x + y)^{r} = x^{r} {(1 + \frac{y}{x})}^{r}$ .

דוגמאות

עבור $r = \frac{1}{2}$ , מתקבלת הנוסחה השימושית:

(1 + x)^{\frac{1}{2}} = \sqrt{1 + x} = 1 + \frac{x}{2} - \frac{x^{2}}{8} + \dots

עבור $r = - 1$ מתקבל הטור הגאומטרי:

(1 + x)^{- 1} = \frac{1}{1 + x} = 1 - x + x^{2} - x^{3} + \dots

הוכחה

הוכחת הנוסחה נעשית באמצעות פיתוח טור טיילור עבור הפונקציה המרוכבת $f (z) = (1 + z)^{r}$ .

ראו גם

קישורים חיצוניים

גדי אלכסנדרוביץ', הבינום של ניוטון, באתר "לא מדויק", שגיאה: זמן שגוי

הבינום של ניוטון

תוכן עניינים