מספר מרוכב

במתמטיקה, מספר מרוכב הוא מספר מהצורה כאשר ו־ הם מספרים ממשיים, ו־ הוא השורש של הפולינום: , כך שמתקיים: .
המספרים המרוכבים יוצרים את שדה המספרים המרוכבים שמסומן בסימן .
כיוון שהריבוע של כל מספר ממשי הוא אי שלילי, למספרים השליליים אין שורש ריבועי. המספרים המרוכבים מתקבלים על ידי "המצאת" מספר שאינו ממשי, , ושילובו במספרים הממשיים. מספרים מרוכבים, כדוגמת , מתקבלים באמצעות הפעולות האריתמטיות הרגילות בין המספרים הממשיים לבין המספר ה"חדש".
שלא כמו במספרים הממשיים, מעל המספרים המרוכבים יש שורש לכל פולינום, לא רק למשוואה , שעל מנת למצוא לה פתרון הוגדר מלכתחילה, אלא גם למשוואות כמו או אפילו . תכונה זו של שדה המספרים המרוכבים מנוסחת במשפט היסודי של האלגברה, והיא שהופכת את המספרים המרוכבים למרכזיים כל כך במתמטיקה המודרנית.
היסטוריה
יצירתם של המספרים המרוכבים, בתחילת המאה ה־16, מיוחסת לג׳ירולמו קרדאנו, שנעזר בהם כדי לפתור את המשוואה ממעלה שלישית. המספרים הוגדרו במפורש, בשנת 1572 על ידי רפאל בומבלי. באותה עת נחשבו מספרים כאלה ללא אמיתיים. מתמטיקאים התקשו לקבל את המושג החדש, והדבר בא לידי ביטוי גם בשם שניתן להם. דקארט, הראשון שהשתמש במושג "מספר מדומה" בשנת 1637, התייחס בכך למה שקרוי כיום "מספר מרוכב". המספרים המרוכבים נכנסו למתמטיקה באופן מלא בעקבות עבודותיהם של אוילר וגאוס.
הגדרה פורמלית של המספרים המרוכבים
כל מספר מרוכב ניתן להציג (באופן יחיד) כסכום , כך ש־ ו־ הם מספרים ממשיים ו־ הוא היחידה המדומה, המקיימת את התנאי . בניסוח זה, נקרא החלק הממשי של המספר, ומסומן ; באופן דומה הוא החלק המדומה של , ומסמנים
מזהים כל מספר מרוכב עם הזוג הסדור (או, באופן שקול, עם נקודה במישור האוקלידי), ומגדירים פעולות חיבור וכפל מיוחדות על נקודות אלו. כתוצאה מכך מתקבל שדה אלגברי. (לפרטים נוספים על הבנייה ראו שדה המספרים המרוכבים ולהסבר כללי על שיטת הרחבה זו ראו הרחבת שדות). ניתן לייצג מספרים מרוכבים בצורה גאומטרית על גבי מערכת צירים קרטזית במישור המרוכב.
בחירת השמות "מספר מדומה" מול "מספר ממשי" מקורה בחוסר האמון שניתן בתחילה למספרים המרוכבים ובתחושה שהם מציאותיים פחות מהמספרים הממשיים. תחושה זו אינה שוללת את תקפותם כמספרים, ובתקופות שונות שרר חוסר אמון גם במספרים השליליים, ואחריהם במספרים הממשיים שאינם רציונליים.
אריתמטיקה של מספרים מרוכבים
המספרים המרוכבים מקיימים
- .
כמו כן נהוג להגדיר:
- ערך מוחלט: – הערך המוחלט מציין את "גודלו" של המספר המרוכב (מרחקו מן הראשית, כאשר מסתכלים על המספר כעל נקודה במישור המרוכב).
- צמוד מרוכב:
ואז מתקיים: . תכונה זו מאפשרת לבצע את פעולת החילוק בין שני מספרים מרוכבים באופן הבא (תחת ההנחה שהמכנה הוא מספר מרוכב שאינו אפס, מה שמבטיח באופן מיידי שגם הצמוד של המכנה הוא מספר מרוכב שאינו אפס): .
את פעולת החיסור בין שני מספרים מרוכבים ניתן להגדיר בקלות בדומה להגדרת פעולת החיבור: .
הצגה קוטבית
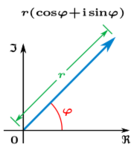
מספר מרוכב שאינו אפס ניתן להציג גם באמצעות המרחק שלו מהראשית והזווית שהוא יוצר עם הכיוון החיובי של הציר הממשי, כלומר עם ציר x (אם המספר הוא אפס, אז הזווית אינה נקבעת באופן יחיד: ניתן לקחת כל זווית שהיא). הצגה זו נקראת הצגה קוטבית (או הצגה פולרית או הצגה טריגונומטרית). על ידי שימוש בטריגונומטריה, ובסימון מקבלים .[1] באמצעות נוסחת אוילר ניתן לכתוב זאת גם כ־ כאשר את הזווית (שנקראת ארגומנט) ניתן לקבל על ידי הנוסחה (הנוסחה נשארת נכונה גם אם , ואז יש שתי אפשרויות, כתלות בסימן של : אם , אז , ואם , אז )[2] ואת (שנקרא הערך המוחלט) על ידי הנוסחה . כמו כן הוא בסיס הלוגריתם הטבעי, על כל התכונות האלגבריות המשתמעות מכך. בחלק מהספרים מסומן לעיתים (כאשר ).
צורת הצגה זו שימושית ביותר. למשל, בהינתן ההצגה הקוטבית של מספר מרוכב פעולות הכפל והחילוק הופכות נוחות ומהירות יותר, מאחר שניתן להיעזר בחוקי חזקות. לדוגמה, בהינתן שני מספרים מרוכבים הנתונים בהצגתם הקוטבית נוכל לבצע את פעולת הכפל ביניהם באופן הבא: . פעולת החילוק תיתן .
מפעולת הכפל בהצגה הפולרית ניתן לראות שכפל במספר מרוכב עם ערך מוחלט 1 וארגומנט , משמעה סיבוב המספר המרוכב הנכפל בזווית .
כמו כן, ניתן להשתמש בנוסחת דה־מואבר (לפיה ) על מנת למצוא שורש של מספר מרוכב (ראו פירוט בערך שורש של מספר).
שימושים
יש בעיות רבות במתמטיקה ובפיזיקה שקל יותר לתאר ולפתור בעזרת מספרים מרוכבים, גם כאשר אין למספרים אלו זכר בניסוח הבעיה ואף לא בתוצאה הסופית שלה.
שימושים במתמטיקה
המספרים המרוכבים הומצאו במקור כדי לפתור משוואות פולינומיות, כגון משוואה ממעלה שלישית, או המשוואה . מאוחר יותר התגלה, שלכל פולינום בעל מקדמים שהם מספרים מרוכבים יש שורש שהוא מספר מרוכב.[3]
באמצעות משפט השארית אפשר לחשב אינטגרלים ממשיים, בייחוד אינטגרלים מוכללים (המכונים גם לא־אמיתיים או לא־נאותים) על כל הישר הממשי: מאפס (או מינוס אינסוף) עד אינסוף.
כמו כן, באמצעות ההצגה הקוטבית ניתן לפתור גם משוואות דיפרנציאליות.[דרושה הבהרה]
פונקציית זטא של רימן, שהיא פונקציה מרוכבת, קשורה באופן מפתיע להתפלגות של מספרים ראשוניים (ראו גם השערת רימן).
דוגמאות לשימושים בפיזיקה ובהנדסת חשמל
בפיזיקה הקלאסית ניתן להשתמש בהצגה הקוטבית של מספרים מרוכבים בפתירת משוואות התנועה של מתנד הרמוני, שהן משוואות דיפרנציאליות. כמו כן הרבה פעמים נוח לחישובים לייצג גלים בצורה מרוכבת (לרוב מתייחסים לחלק הממשי בלבד כגודל בעל משמעות פיזיקלית).
במכניקת הקוונטים, בסיס המצבים של כל מערכת כלול במרחב הילברט מעל המספרים המרוכבים. לכל פונקציית גל יש מופע מרוכב שלא משפיע על גודל המשרעת שלה אלא רק על "כיוון" הגל, ומאפשר לה להתאבך עם פונקציות גל אחרות. אף על פי כן, ההסתברות למדידת גודל פיזיקלי מדיד מסוים היא תמיד ממשית ולא־שלילית.
מספרים מרוכבים שימושיים במיוחד גם בתיאור גדלים מחזוריים, באופטיקה פיזיקלית, בתורת החשמל ובהנדסת אלקטרוניקה. בתחומים אלה משתמשים בפאזורים (גדלים מרוכבים הכוללים משרעת ומופע). בשני התחומים האחרונים נהוג לסמן את החלק המרוכב באות במקום באות , הואיל וזו כבר משמשת בהם לסימון זרם.
ראו גם
- i (מספר)
- הכללות של המספרים המרוכבים: אלגברת קווטרניונים (ובפרט אלגברת הקווטרניונים של המילטון), אלגברת אוקטוניונים (ובפרט אלגברת האוקטוניונים של קיילי).
קישורים חיצוניים
- מספר מרוכב, באתר MathWorld (באנגלית)
- מספר מרוכב, באתר אנציקלופדיה בריטניקה (באנגלית)
- מספר מרוכב, באתר אנציקלופדיה למתמטיקה (באנגלית)
- גדי אלכסנדרוביץ', הכי ממשיים שיש: הכירו את המספרים המרוכבים, באתר ynet, 11 באוקטובר 2011
- מיכאל גורודין, האם יש מספרים לא אמיתיים?, במדור "מדע במבט-על" באתר של מכון דוידסון לחינוך מדעי, 26 באפריל 2022
 אלגברה א - הרצאה 05, סרטון בערוץ "Technion", באתר יוטיוב (אורך: 45:59) – הרצאה מצולמת על המספרים המרוכבים מאת פרופ׳ דוד צילג, מתוך ספריית הווידאו של הטכניון – אלגברה א׳
אלגברה א - הרצאה 05, סרטון בערוץ "Technion", באתר יוטיוב (אורך: 45:59) – הרצאה מצולמת על המספרים המרוכבים מאת פרופ׳ דוד צילג, מתוך ספריית הווידאו של הטכניון – אלגברה א׳ מספרים מרוכבים, דף שער בספרייה הלאומית
מספרים מרוכבים, דף שער בספרייה הלאומית
הערות שוליים
- ↑ או בקצרה
- ↑ הגדרה זו של אינה לגמרי מדויקת: הזווית בהצגה הקוטבית מהווה באופן כללי את הסטייה ברדיאנים מציר x החיובי במישור המרוכב, הנמדדת לפי הכיוון המנוגד לכיוון השעון. כיוון שהתמונה של הפונקציה היא , היא לא מכסה את כל טווח הערכים האפשרי לזווית . ניתן לראות זאת גם על ידי כך שההגדרה לא מבדילה בין הזווית המתקבלת ממספר מהצורה לבין זו שמתקבלת מהמספר . לצורך התיקון, כאשר החלק הממשי של המספר שלילי, מגדירים . לטיפול מלא בבעיית קביעת הזווית, ראו קואורדינטות קוטביות#מציאת הזווית.
- ↑ בהקשר זה, מספר מרוכב שהחלק המדומה שלו שווה לאפס שקול למספר ממשי.
| אנליזה מרוכבת | ||
|---|---|---|
| בסיס | מספר מרוכב • שדה המספרים המרוכבים • המשפט היסודי של האלגברה • הספירה של רימן • נוסחת אוילר (אנליזה מרוכבת) | |
| פונקציות | פונקציה מרוכבת • פונקציה שלמה • פונקציה אנליטית • פונקציה הולומורפית • פונקציה אוניוולנטית • נוסחת אוילר • העתקת מביוס • משפט ההעתקה של רימן | |
| נגזרות | משוואות קושי-רימן • העתקה קונפורמית • טור לורן | |
| אינטגרל | משפט ההערכה • משפט האינטגרל של קושי • נוסחת האינטגרל של קושי • משפט מוררה • משפט ליוביל | |
| סינגולריות | סינגולריות • סינגולריות סליקה • קוטב • סינגולריות עיקרית • משפט קזוראטי-ויירשטראס • נקודת הסתעפות | |
| משפט השאריות | משפט השאריות • עקרון הארגומנט • משפט רושה | |
| עקרון המקסימום | עקרון המקסימום • למת שוורץ • משפט הערך הממוצע של גאוס | |
| אנליזה מתמטית • חשבון אינפיניטסימלי • אנליזה וקטורית • טופולוגיה • אנליזה מרוכבת • אנליזה פונקציונלית • תורת המידה | ||
| מערכות מספרים | ||
|---|---|---|
| מספרים | המספרים הטבעיים (מערכת פאנו) • חוג המספרים השלמים (מספרים חיוביים ושליליים, מספר שלם) • שדה המספרים הרציונליים (מספר רציונלי, מספר אי-רציונלי) • שדה המספרים הממשיים (הישר הממשי, מספר ממשי) • שדה המספרים המרוכבים (המישור המרוכב, מספר מרוכב, מספר מדומה) | |
| הרחבות של חוג המספרים השלמים | חוג השלמים של גאוס • חוג השלמים האלגבריים • חוג השלמים של אייזנשטיין | |
| הרחבות של שדה המספרים הרציונליים | שדה מספרים • שדה המספרים הניתנים לבנייה • שדה המספרים האלגבריים (מספר אלגברי, מספר טרנסצנדנטי) • שדה המספרים ה-p-אדיים (מספר p-אדי) • שדה ציקלוטומי | |
| מעבר למרוכבים | אלגברת קווטרניונים (אלגברת הקווטרניונים של המילטון ) • אלגברת אוקטוניונים (אלגברת האוקטוניונים של קיילי ) • אלגברות קיילי-דיקסון | |
מספר מרוכב40902086Q11567


