פיתוח לפלס למולטיפולים אלקטרוסטטיים
בפיזיקה, פיתוח לפלס למולטיפולים אלקטרוסטטיים (באנגלית: Laplace electrostatic potential expansion) הוא פיתוח הנועד לתאר את השפעותיו של קובץ מטענים אלקטרוסטטיים בהתפלגות כלשהי, וממנו ניתן לחשב את הפוטנציאל החשמלי, השדה החשמלי, הכוח החשמלי וכיוצא באלה. בין פיתוח זה לבין פיתוח לפלס עבור שדה כבידה ישנו דמיון רב, ובאופן כללי כוחו יפה לכל שדה פוטנציאל שהאלמנט הבסיסי שלו מייצר פוטנציאל הדועך כמו , עם השינויים המתאימים. ערך זה מתמקד בפיתוח לפלס למולטיפולים חשמליים. שמו של הפיתוח נגזר מכך שהוא הפתרון לבעיית לפלס במרוחק ממערך מטענים אלקטרוסטטיים בהתפלגות כלשהי, שהוא גם הפתרון לבעיית פואסון באזור המרוחק בו כבר אין מטענים.

מניתוח השפעת אלמנטי מטען מורכבים, נובע שלכל סוג של אלמנט טעון חשמלית, הקווים שווי הפוטנציאל בתרשים הדו־ממדי שונים באופיים מקווי הפוטנציאל בכל אחד משאר המקרים. קיים הבדל בצורת ההתפשטות, ממנה ניתן לגזור את כיוני השדה החשמלי, ובדעיכת צפיפות הקווים, המעידה על דעיכה של ערך הפוטנציאל באותו אזור. הניתוח המולטיפולי של השפעת מערך מטענים בנקודה רחוקה, מתמקד בעיקר באופי הדעיכה, השונה מאלמנט לאלמנט, בעיקר בהתייחס למערך רציף של מטענים, הסדר המוביל[1] בפיתוח המולטיפולי, הסדר הראשון שלא מתאפס, מלמד על התנהגות הפוטנציאל המרחבי הנוצר. פעמים רבות, דרך זו של מציאת הפוטנציאל המרחבי, תהיה עדיפה בהרבה על פתרון בעיית לפלס (עם תנאי השפה של האזור בתוכו מתפלגים המטענים), כאשר אנו מעוניינים בפתרון עבור נקודה מרוחקת.
הפיתוח למומנטים
התפלגות אלקטרוסטטית רציפה

גודל הפוטנציאל החשמלי שיוצר מערך רציף של מטענים אלקטרוסטטיים, שסכומם האלגברי הכולל מתאפס (כמתואר באיור), בנקודה מרוחקת , כאשר התווך הוא ריק, ולכן ערכו של הקבוע הדיאלקטרי במקרה זה הוא , מחושב כך:
יהי אזור מרחבי עם התפלגות המטען . ללא הגבלת הכלליות נבחר את ראשית הצירים להיות בנקודה כמתואר, כך שהמרחק בין לאלמנט מטען ב- יהיה , המרחק מהראשית ל- יהיה והזווית בין ל- תהיה .
ממילא המרחק בין אלמנט מטען ב- ל- הוא:
ובמצב זה אלמנט פוטנציאל בנקודה , הנוצר מאלמנט מטען באזור , יהיה: כאשר לעיל השתמשנו בפונקציה היוצרת של פולינומי לז'נדר, עבור .
לאחר סופרפוזיציה מרחבית, הפוטנציאל הכולל בנקודה יהיה הסכום של כל אלמנטי הפוטנציאל, כלומר: כאשר הוא היעקוביאן השווה ל- בקואורדינטות קרטזיות או ל- בקואורדינטות כדוריות.
התפלגות אלקטרוסטטית בדידה
עבור מערך מטענים בדיד נוכל להשתמש בפיתוח הרציף כאשר ההתפלגות תהיה התפלגות דלתא כפונקציונל ליניארי עבור פתרון דיסטריבוטיבי. כלומר, תיאור צפיפות המטען במרחב עם מטען נקודתי ב- יהיה:
כאשר היא הדלתא של דיראק.
עבור מערך מרובה מטענים, כאשר מתאר את מספר המטענים , מתקיים:
המומנטים הראשונים בפיתוח המולטיפולי
מבחינה מעשית נוכל להסתפק בסדר המוביל בפיתוח למולטיפולים חשמליים, כדי לקבל קירוב טוב לביטוי לפוטנציאל בנקודה מרוחקת. בדרך כלל נתעניין בסדרים הראשונים, שבמקרים רבים מספיקים על מנת לתאר מערכת אלקטרוסטטית ואת השפעותיה במרחב (דהיינו את הפוטנציאל החשמלי וכל הנגזר מכך). על מנת להקל על הטיפול במערכות מטענים סטטיות מסובכות, הוגדרו ארבעה אובייקטים (מומנטים) המאפיינים את ארבעת הסדרים הראשונים דלעיל: המומנט הראשון נקרא המונופול והוא הגודל הסקלרי , המומנט השני הוא מומנט הדיפול המוגדר להיות הווקטור , המומנט השלישי הוא הקוואדרופול המאופיין על ידי מטריצת מומנט הקוואדרופול של טנזור סימטרי מסדר שני, והרביעי הוא מומנט האוקטופול שייצוגו בכתיב טנזורי תלת־ממדי (מסדר שלישי) הוא כאשר היא פונקציית הדלתא של קרונקר (להבדיל מהדלתא של דיראק בה עשינו שימוש בחלק הקודם). על ארבעת אלה ועל תכונותיהם נפרט בהמשך.
נעיר כי ניתן, תחת ההגדרות לעיל, להציג את הביטוי לפוטנציאל החשמלי באופן הבא: כאשר היא עכבת מטריצת מומנט הקוואדרופול ו- הוא הרכיב ה- של וקטור היחידה בכיוון .
המונופול
מונופול מייצג חלקיק נקודתי חד-קוטבי שיכול להיות טעון חיובי או שלילי. יחידות המונופול הן קולון ( ).
הפוטנציאל החשמלי שיוצר חלקיק נקודתי (ביחס לכל סקלת אורך) טעון מסומן ובריק הוא נתון על ידי הנוסחה . בנוסף השדה החשמלי שיצור אותו מטען מסומן וערכו וכתוצאה משדה אלקטרוסטטי זה יפעל כוח שיהיה כוח דחייה אם המטענים שווי סימן, וכאשר הם מנוגדי סימן כוח זה יהיה כוח משיכה, כך שערכו המתקבל יהיה בסימן שלילי.
באופן דומה ניתן להתייחס לצבר מטענים נקודתיים מרוכזים (באזור המרוחק מנקודת המדידה) שמומנט המונופול שלהם הוא וממנו נגזרים הפוטנציאל, השדה, הכוח, והאנרגיה האלקטרוסטטיים.
הדיפול
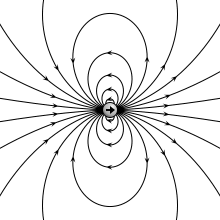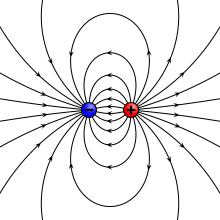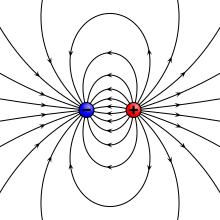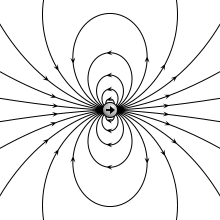
הדיפול כאלמנט מוגדר כשני מטענים נקודתיים שווי ערך ומנוגדי סימן המרוחקים האחד מהשני מרחק המהווה את גודלו של הווקטור המכוון מהמטען הנקודתי השלילי אל המטען הנקודתי החיובי[2]. יחידותיו של מומנט הדיפול הן קולון במטר ( ).
מומנט הדיפול הוא הווקטור כאשר הוא ערכו (המוחלט) של כל אחד משני המטענים המרכיבים את הדיפול. הפוטנציאל שיוצר אלמנט דיפול יחיד במערכת צירים פולרית, כאשר המטען בנקודה והמטען בנקודה , הוא , וכיוון ש- , השדה החשמלי באותן קואורדינטות קוטביות הוא . כלומר לשדה החשמלי הנוצר מאלמנט בודד של דיפול יש רכיב בכיוון , אך גם בכיוון , ושני הרכיבים הם:
וכל אחד מהם דועך בקצב של , בניגוד לדעיכת שדה ממונופול הדועך כ- .
בקואורדינטות כדוריות נקבל תוצאה דומה, רק שהפעם .
במצבים בהם המדידה מתבצעת בנקודה רחוקה אך לא מספיק כדי להתייחס למערך כנקודתי, או לחלופין כאשר חישוב מומנט המונופול מתאפס, ניקח בחשבון את מומנט הדיפול- חישוב המתחשב בהשפעתם של כל זוג מטענים שווי ערך ומנוגדי סימן הקרובים זה לזה כך שכמעט מבטלים את ההשפעות אחד של השני בנקודה מרוחקת ובלבד ש- איננו גדול מדי. כלומר עבור צבר דיפולים המתהווים מהתפלגות מטען נקודתי כלשהי, מומנט הדיפול יהיה- וניתן לראות את השקילות המתחייבת (על מנת שנוכל לייצג את בצורה לעיל) להגדרה של מומנט הדיפול, שהרי אם הוא אינדקס המצביע על כל מטעני ו- הוא אינדקס הרץ על כל שאר מטעני (כך ש- הוא אינדקס הרץ על כל מטעני המערך)- אזי כיוון ש- , ברור כי-
הקוואדרופול

הקוואדרופול הוא המומנט השלישי בפיתוח למולטיפולים, והוא יכול להיות מיוצג בשני סוגים של אופנים- חד־ממדי (כמו הצגת הדיפול) הנקרא קוואדרופול ליניארי, או דו־ממדי שהוא קוואדרופול קלסי, כמתואר באיור. עבור שתי תצורות אלו ייווצר, הרחק מהן, פוטנציאל חשמלי שבו הסדר המוביל הוא המולטיפול השלישי. יחידות מומנט הקוואדרופול הן .
בקואורדינטות פולריות ניתן לבטא את הפוטנציאל החשמלי הנוצר (בנקודה רחוקה) למשל כתוצאה מאלמנט קוואדרופול ליניארי על ידי- ואפשר לראות שהפוטנציאל דועך כמו , לעומת בדיפול ו- במונופול.
גם כאן ניתן להכליל למקרה של מערך רציף (בעל אופי של קוואדרופול[3]) עם התפלגות מטען , כך שתיאור הפוטנציאל החשמלי המרחבי במערכת צירים כדורית יהיה- כך שאם נציב מיד יתקבל הביטוי- כאשר ו- .

לעיתים מתייחסים למומנט הקוואדרופול כגודל הסקלרי המאפיין אותו, על אף שאין זה ייצוגו המדויק. כיוון שהקוואדרופול הוא טנזור מסדר שני, ניתן לתאר אותו בעזרת מטריצה דו־ממדית של שמתוך מרכיביה הם בלתי תלויים, אך כמובן ניתן להצגה גם בכתיב טנזורי כאשר:
ואז פוטנציאל מומנט הקוואדרופול יראה כך-
כאשר היא מטריצה חסרת עכבה המאפיינת את מומנט הקוואדרופול ולה רכיבים בלתי תלויים מתוך .
ממילא ניתן לראות כי כאשר נחשב את מינוס הגרדיאנט של הביטוי הנ"ל, נקבל את שלושת רכיביו של השדה החשמלי, בכיוונים , ו- .
האוקטופול, ההקסטודופול ומולטיפולים מסדרים גבוהים

המומנט הרביעי בפיתוח המולטיפולי הוא של האוקטופול. לאוקטופול לרוב יהיה מבנה מורכב משל הקוואדרופול, וניתן לייצגו בכמה תצורות על ידי מערך סופי של מטענים נקודתיים. הדרך הקלאסית ליצור פוטנציאל המתנהג ודועך כמו הסדר הרביעי בפיתוח למולטיפולים היא על ידי שני קוואדרופולים האחד מול השני כאשר באחד מהם מחליפים בין המטענים החיוביים והשליליים. מומנט האוקטופול יכול להיות מיוצג על ידי מטריצה תלת־ממדית מסדר שלישי (מטריצה שממדיה הם ), או על ידי טנזור מסדר שלישי עם רכיבים. יחידותיו של מומנט האוקטופול הן .
לפעמים נרצה להתכנס לרמת דיוק גבוהה בחישוב הפוטנציאל החשמלי המרחבי, או שאחרת נקבל תוצאה טריוויאלית, ולכן נצטרך לחשב את הסדר הרביעי בפיתוח לפוטנציאל. במצב כזה ניקח בחשבון את הביטוי- ונציג אותו בצורה נוחה על ידי:

כך שסדר האוקטופול בפיתוח המולטיפולי לפוטנציאל הוא פשוט- או לחלופין, כיוון ש- , נתכנס להצגה המקובלת: ובהתאם לפיתוח מתקבל פוטנציאל חשמלי הדועך כמו ולכן השדה החשמלי ידעך כמו .

האוקטופול הוא האחרון ברביעיית הסדרים הראשונים שניתן לייצגם במרחב אוקלידי תלת־ממדי (על ידי מערך בדיד, סימטרי ואחיד[4]) בתהליך רקורסיבי פשוט של הוספת (במקביל) היפוך השיקוף של אלמנט המומנט הקודם (למעט במונופול שהוא תנאי ההתחלה של התהליך הרקורסיבי) לקבלת אלמנט בסיס למומנט הנוכחי כקודקודיו של מצולע משוכלל (עם אותו ממד ליניארי כך ש- ).
הסימטריה הנ"ל אינה נשמרת במובן שלא ניתן למשל ליצור אלמנט הקסטודופול (אלמנט עם ) כקודקודיו של טסרקט (גוף במרחב ארבע-ממדי המהווה היפרקובייה מממד 4) במרחב תלת־ממדי (זאת כיוון שבמרחב כזה ניתן לתאר בסך הכל גאומטריה של ממד אפס, חד־ממד, דו־ממד ותלת־ממד).
כתוצאה מכך, תיאור של מומנט כאלמנט נעשה מסובך ככל שמתקדמים לסדרים הגבוהים (שהולכים ונעשים זניחים, בקצב דעיכה של כאשר הוא סדר המולטיפול והוא שווה ל- כאשר מדובר במונופול), למשל כמו ההקסטודופול (המיוחס לסדר החמישי בפיתוח המולטיפולי ולו טנזור רב ממדי (מסדר רביעי) עם רכיבים, ודעיכת פוטנציאל כמו ושדה כ- ).
ראו גם
לקריאה נוספת
- Griffiths, David J. (2007) Introduction to Electrodynamics, 3rd Edition
- David K. Cheng (1989) Field and Wave Electromagnetics, 2nd Edition
- W. J Duffin (1990) Electricity and magnetism, 4nd Edition
- J. B. Tatum (2006) Dipole and Quadrupole Moments, Electricity and Magnetism
- Glenn Rowe (2012) Quadrupole moment, Electrodynamics
קישורים חיצוניים
- Dipole and Quadrupole Moments, באתר Physics topics
- יסודות הפיתוח המולטיפולי בבלוג רשימות בפיזיקה עיונית.
הערות שוליים
- ↑ בפעמים מסוימות (לא בערך זה) מקובל לאפיין את 'הסדר המוביל' כאיבר הראשון שלא מתאפס בפיתוח לטור לורן.
- ↑ האזכור דיפול מתייחס לעיתים למומנט הדיפול.
- ↑ דהיינו מערך מטענים שבהסתמך על מדידות (בנקודה מרוחקת) ניתן לדמות אותו לאלמנט קוואדרופול בודד.
- ↑ במובן שערכם המוחלט של כל אחד מאלמנטי המטען הנקודתיים שווה.
פיתוח לפלס למולטיפולים אלקטרוסטטיים42254577Q18192606


