גלגול (מכניקה)

ההנפשה מתארת את תנועת הגלגול כסופרפוזיציה של שתי תנועות: העתקה של הגלגל ביחס למשטח, וסיבוב של הגלגל ביחס לעצמו.

האיור מציג את המהירויות הרגעיות בנקודות שונות על פני דיסקה מתגלגלת

במכניקה, גלגול הוא סוג של תנועה המתקיימת כאשר שני גופים, שקיים מגע רצוף ביניהם, נעים האחד ביחס לשני בתנועה המשלבת סיבוב והעתקה, באופן שהמהירות היחסית הרגעית, בנקודת המגע של הגופים, שווה לאפס. בדרך כלל מקובל להתייחס לתנועה שבה לאחד מהגופים יש סימטריה צירית, בעוד הגוף האחר הוא משטח ישר, כמו למשל, גלגול של כדור או גלגל על רצפה, אם כי, תתכנה גם אפשרויות אחרות. בתנאים אידאליים, שטח המגע בין הגופים מצטמצם לנקודה אחת בלבד (או לקו ישר, במקרה של גליל או חרוט), ולא מתקיימת החלקה. תנועת גלגול כזו נקראת גלגול טהור. במציאות, עקב עיוותים באזור המגע, מתקיימת תמיד מידה מסוימת של החלקה. כתוצאה מכך, וכתוצאה מתהליכים פנימיים נוספים, חלק מהאנרגיה הקינטית האצורה במערכת הופך לחום.

פיזיקה של תנועת גלגול פשוטה

שדה המהירויות של גלגל, בקו הכולל את נקודת המגע ומרכז המעגל. המהירות בנקודת המגע שווה לאפס והולכת וגדלה באופן לינארי ככל שהמרחק מנקודה זו גדל

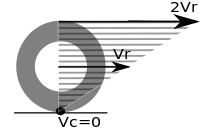
תנועת הגלגול הפשוטה ביותר היא של דיסקה מעגלית קשיחה, המתגלגלת ללא החלקה, על גבי משטח ישר ונייח, כשציר הסימטריה שלה מקביל למשטח. תנועה זו משלבת תנועה סיבובית של הדיסקה סביב ציר הסימטריה שלה, ותנועה של ציר הסימטריה עצמו במקביל למשטח. המהירות הקווית הרגעית של כל נקודה בדיסקה זהה למהירות שהייתה מתקבלת אם אותה דיסקה הייתה מסתובבת סביב ציר נייח העובר דרך נקודת המגע שלה עם המשטח. מכאן נובע שמהירות נקודת המגע ביחס למשטח שווה לאפס, ומהירות הנקודה המרוחקת ביותר מנקודת המגע כפולה מזו של ציר הסימטריה. מהירותה הרגעית של כל נקודה בדסקה נתונה במשוואה:

$\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}$

כאשר $\overrightarrow{r}$ הוא וקטור המרחק בין הנקודה לנקודת המגע ו־$\overrightarrow{\omega }$ הוא וקטור המהירות הזוויתית של הגוף.

המסלול אותו מתווה כל נקודה על פני היקף הדיסקה נקרא ציקלואידה.

מקרים מיוחדים

חרוט מתגלגל על פני חרוט אחר. תנועת החרוט הנייד מורכבת משתי תנועות סיבוביות: סביב ציר הסימטריה של החרוט הנייח, וסביב ציר הסימטריה של עצמו.

תנועת גלגול של דיסקה על פני דיסקה אחרת. ייתכנו שני מקרים:

1. דיסקה אחת נייחת והדיסקה השנייה מתגלגלת על פניה. זהו מצב אקוויוולנטי לגלגול של דיסקה על פני משטח ישר, פרט לעובדה שבמקרה זה המשטח הוא מעגלי.
2. צירי הסיבוב של שתי הדיסקיות נייחים, והדיסקיות מסתובבות בכוונים מנוגדים. במקרה זה, המהירות הרגעית בנקודת המגע אינה שווה לאפס, והמהירות בשתי נקודות המרוחקות ביותר מנקודת המגע שווה למהירות בנקודת המגע, והפוכה לה בכיוונה. ייתכן מקרה שבו את מקום אחת מהדיסקיות תופס זיז (גוף שאינו סימטרי). במצב זה, מכיוון שהמרחק בין נקודת המגע לציר הסיבוב של הזיז אינו קבוע, ציר הסיבוב של לפחות אחד מהגופים חייב לקיים תנועה רדיאלית.

תנועת גלגול של חרוט על פני חרוט אחר. במקרה זה אחד החרוטים חייב להיות קמור בעוד האחר יכול להיות קעור, קמור, או משטח ישר (זהו בעצם מקרה פרטי של חרוט שזווית הראש שלו שווה ל- $\pi$). ייחודה של תנועת הגלגול של חרוט היא, שמרכז המסה שלו מבצע תנועה מעגלית בניגוד לדיסקה, או גליל, שמרכז המסה שלהם נע בקו ישר. ייחוד נוסף הוא שקיימת נקודה על פני החרוט, (הקדקוד שלו), הנמצאת במנוחה במהלך התנועה כולה.

גלגול של גופים חסרי סימטריה צירית. תנועת גלגול אינה מותנית בכך ששני הגופים, או אפילו אחד מהם, יהיו בעל סימטריה צירית. שתי דוגמאות ידועות הן משולש רולו (Reuleaux triangle) וגופי מייסנר (Meissner bodies). הספריקון (Sphericon) והאולואיד (Oloid) הם חברים בקבוצה מיוחדת של גופים מתגלגלים, שבמהלך תנועתם פורשים את כל שטח הפנים שלהם, כך שבמהלך כל מחזור גלגול, כל נקודה על פני השטח שלהם נוגעת במשטח עליו הם מתגלגלים.

שימושים

כיון שבאזור המגע של שני גופים המתגלגלים זה על גבי לזה, כמעט ולא מתקיימת תנועה יחסית, כוח החיכוך הקינטי המתנגד לתנועה הוא מזערי. ניתן לנצל זאת בהתקנים בהם נדרשת תנועה יחסית בין רכיבים הנמצאים במגע זה עם זה.

גלגל. הגלגל הוא המוצר העתיק ביותר, והנפוץ ביותר, המנצל את היתרונות המכניים הגלומים בתנועת גלגול. כיון שכוח החיכוך הנוצר בתנועה זו נמוך במאות אחוזים מכוח החיכוך הנוצר בתנועת החלקה, מאפשר השימוש בגלגל לשנע מטענים ממקום למקום תוך השקעה של אנרגיה מינימלית.

מסב גלילה. מסב גלילה הוא חלק במכונה שמטרתו, בין היתר, למזער את כוח החיכוך בין שני אלמנטים של המכונה הנעים האחד ביחס לשני. המסב בנוי, בדרך כלל, משתי טבעות קונצנטריות, שביניהן נמצאים גופי גלילה בעלי סימטריה צירית, כגון כדורים, גלילים, חרוטים וכו'. כל אחת מהטבעות מחוברת לאלמנט אחר של המכונה, ובשעה שאחד האלמנטים, או שניהם, נמצאים בתנועה, מתחילים גופי הגלילה להתגלגל על פני שתי הטבעות בו זמנית, ומאפשרים הפחתה של ממש בכוח החיכוך.

גלגל שיניים. גלגל שיניים הוא חלק במכונה שמטרתו לאפשר העברת מומנט בין שני צירים, או יותר, במכונה. בהיקפם של גלגלי השיניים נמצאות בליטות (השיניים), המתוכננות באופן כזה שכאשר שני גלגלי שיניים משולבים ונעים בתנועה סיבובית האחד ביחס לשני, הבליטות של גלגל אחד נעות בתנועת גלגול מושלמת על פני הבליטות של הגלגל השני.

גלגלת. גלגלת היא מתקן שמטרתו לאפשר שינוי בכוונו של כבל משיכה, באופן שממזער את התנגדות כוח החיכוך. בהיבט של תנועת הגלגול זהו מקרה מיוחד בו אחד העצמים במערכת (הכבל) הוא גמיש, ולכן מתקיים מצב בו בין שני גופי המערכת (הגלגל והכבל) קיים מגע לאורך קו, ולא מגע נקודתי בלבד. מצב דומה ניתן למצוא גם בכלי רכב זחליליים ובמסועים.

לקריאה נוספת

• Halliday, David; Resnick, Robert (2013), Fundamentals of Physics, Chapters 10, 11: Wiley

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

שגיאות פרמטריות בתבנית:קצרמר
פרמטרי חובה [ 1 ] חסרים

ערך זה הוא קצרמר. אתם מוזמנים לתרום למכלול ולהרחיב אותו.