בנייה (גאומטריה)
בגאומטריה, בנייה היא שרטוט של עצמים גאומטריים, כגון קטעים בעלי תכונות מוגדרות, על פי כללים נתונים.
הבנייה הבסיסית בגאומטריה אוקלידית היא בנייה בסרגל ובמחוגה. קיומן של בעיות בנייה שאינן ניתנות לפתרון בכלים אלה הוביל להצעתם של כלי בנייה נוספים, שיאפשרו לפתור בעיות אלה. מאידך ניתנו הוכחות לכך שבעיות בנייה שניתן לפתור בסרגל ובמחוגה ניתן לפתור גם באמצעים מצומצמים יותר.
בנייה בסרגל ובמחוגה
ערך מורחב – בנייה בסרגל ובמחוגה
הבנייה הבסיסית בגאומטריה אוקלידית היא בנייה בסרגל ובמחוגה, כלומר בנייה המשתמשת בסרגל ובמחוגה בלבד. לעניין זה, הסרגל והמחוגה אינם הכלים הפיזיים המשמשים בשרטוט, אלא הפשטות גאומטריות, המממשות את שלוש ההנחות הראשונות מבין חמש ההנחות של אוקלידס ב"יסודות":
- הסרגל הגאומטרי הוא כלי המאפשר יצירת קו ישר או קטע ארוך כרצוננו העובר דרך שתי נקודות נתונות. לסרגל אין יכולת מדידה (לא מסומנות עליו שנתות המציינות יחידות אורך), וההנחה היא שאי אפשר ליצור עם הסרגל לבדו שני ישרים מקבילים במרחק נתון זה מזה.
- המחוגה הגאומטרית מאפשרת להתוות מעגל שמרכזו הוא נקודה נתונה, ורדיוסו נתון או שווה למרחק בינה לבין נקודה אחרת.
פעולות אפשריות
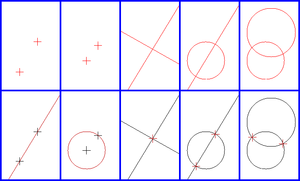
סרגל ומחוגה מאפשרות לבצע שתי פעולות יסודיות:
- שרטוט ישר (ארוך כרצוננו) שעובר דרך שתי נקודות נתונות
- שרטוט מעגל שמרכזו בנקודה נתונה, והוא עובר דרך נקודה נתונה אחרת.
בנוסף לזה אפשר למצוא את:
- נקודת החיתוך של שני ישרים (שאינם מקבילים)
- נקודות החיתוך של ישר ומעגל (אם קיימות)
- נקודות החיתוך של שני מעגלים (אם קיימות)
בניה במחוגה וסרגל היא שרשרת של פעולות כאלו, המגיעה אל התוצאה המבוקשת.
הבעיות הגאומטריות של ימי קדם
- ערך מורחב – הבעיות הגאומטריות של ימי קדם
היוונים הקדמונים ניסחו ארבע בעיות, אשר במשך כ-2,000 שנה היו בעיות פתוחות:
- הכפלת הקובייה: בניית קובייה שנפחה כפול מהנפח של קובייה נתונה
- תרבוע המעגל: בניית ריבוע השווה בשטחו למעגל נתון
- שילוש זווית: חלוקת זווית נתונה לשלושה חלקים שווים
- בנייה של משובע משוכלל
כל ארבע הבעיות הוכחו כבלתי פתירות בבנייה בסרגל ובמחוגה, באמצעות יישום אלמנטרי של התורה המתמטית העוסקת בהרחבת שדות.
צמצום ארגז הכלים
למרות שבבעיות הבנייה הקלאסיות מקובל היה להשתמש בשני הכלים, הסרגל והמחוגה, ידוע שאפשר להסתפק בפחות. בשנת 1797 פרסם הגאומטרן האיטלקי לורנצו מסקרוני ספר, שבו הראה שכל בעיה שאפשר לבנות בסרגל ומחוגה, אפשר לבנות גם באמצעות המחוגה לבדה[1]. כדי להראות זאת, הוכיח מסקרוני שבמחוגה ניתן לחבר ולחסר ארכי קטעים, וגם להכפיל ולחלק אורכים זה בזה. (לא ניתן לבנות ישרים, אך ניתן למצוא שתי נקודות המתוות את הישר, ולמעשה לשרטט נקודות כרצוננו הנמצאות על הישר).
כבר ב- 1759 עסק ד'אלמבר בפתרון בעיות בנייה בסרגל בלבד. בעיות אלה מטבען מוגבלות יותר מאשר הבניות במחוגה ובסרגל, משום שהסרגל אינו מאפשר אלא פתרון של משוואות ליניאריות. עבודתו של ד'אלמבר המריצה מתמטיקאים צרפתיים אחרים לעסוק בנושא, שהעניין בו גבר אחרי פרסום ספרו של מסקרוני. באותה עת הציע ז'אן-ויקטור פונסלה (Jean-Victor Poncelet ; 1867-1788) שהוספת מעגל אחד קבוע במישור (יחד עם המרכז של אותו מעגל), די בה כדי לאפשר לסרגל לפתור כל בעיית בנייה במחוגה וסרגל. השערה זו הוכחה ב-1833 על ידי הגאומטרן יאקוב שטיינר, וזכתה לשם משפט פונסלה-שטיינר.
הרחבת ארגז הכלים
קיומן של בעיות בנייה שאינן ניתנות לפתרון בסרגל ובמחוגה הוביל להצעתם של כלי בנייה נוספים, שיאפשרו לפתור בעיות אלה.
כלי נוסף שניתן להגדיר הוא "סרגל דו-צדדי" ― כלי שבהינתן ישר, מסוגל לבנות ישר מקביל במרחק קבוע (רוחב הסרגל), ובהינתן שתי נקודות שמרחקן גדול מרוחב הסרגל, מסוגל לבנות ישר דרך אחת מהן שמרחקו מהשנייה שווה לרוחב הסרגל. כל בעיה שאפשר לבנות בסרגל ומחוגה, אפשר לבנות באמצעות סרגל דו-צדדי בלבד.[2]
היפיאס הראה שבעזרת קוואדרטריקס, כלי שאיננו בארגז הכלים של הגאומטריה, ניתן לחלק זווית נתונה לשלושה חלקים, וכן הוכח שכלי זה מאפשר את תרבוע העיגול.
כלי אחר שנעשה בו שימוש בהקשר דומה, הוא "הסרגל המסומן" או ה-neusis construction (אנ'), כלי שבהינתן קטע, נקודה, ושני קווים, בונה נקודה על כל אחד מהקווים כך ששלוש הנקודות ― הנתונה ושתי החדשות ― נמצאות על ישר אחד, והמרחק בין שתי החדשות הוא כאורך הקטע הנתון. כלי זה ניתן ל"מימוש" על ידי סרגל, עליו ניתן לסמן אורך של קטע נתון, ואז להניח אותו על הנקודה הנתונה, ולאפשר לו להסתובב ולהחליק על גביה, עד ששני קצות הקטע שמסומן עליו ייגעו בשני הקווים הנתונים ― ואז לבנות את הקו שהוא מתווה.
ה-neusis construction מספק פתרון נאה לכמה מהבעיות שהוזכרו קודם לכן, כמו הבעיה של הכפלת הקובייה (אותה אפשר לפתור גם באמצעות חיתוך של פרבולות, או בעזרת העקום הקרוי קונכואיד, שבנייתו מיוחסת לניקומדס, בן המאה השנייה לפני הספירה). ארכימדס הראה שאפשר, בעזרת סרגל, מחוגה ו-neusis construction, לחלק זווית נתונה לשלושה חלקים.
ניתן להגדיר עקום שלישי זווית (אנ'), ואז בעזרת סרגל ומחוגה לחלק זוויות ל-3 חלקים שווים.
קישורים חיצוניים
הערות שוליים
- ^ בנייה באמצעות מחוגה בלבד
- ^ סנדרה קיי בירל, עבודת גמר לתואר מוסמך במכון הטכנולוגי של קליפורניה, מאי 1983. העבודה עוסקת בכלים נוספים; הפרק שנוגע לסרגל הדו צדדי מתחיל בעמוד 50.
38541043בנייה (גאומטריה)