הבעיה העשירית של הילברט
הבעיה העשירית היא אחת מעשרים ושלוש הבעיות שהציג דויד הילברט בקונגרס המתמטי של שנת 1900. בעיה זו היא מהבעיות המפורסמות ביותר במתמטיקה של המאה ה-20, ותולדותיה הן אבני דרך בולטות בהתפתחות הלוגיקה המתמטית ומדעי המחשב התאורטיים. הדרישה שהציגה הבעיה:
- ”למצוא אלגוריתם שיקבע האם למשוואה דיופנטית פולינומית נתונה יש פתרון במספרים טבעיים.”
(הילברט הציג את הבעיה שלו עבור מספרים שלמים. אולם אפשר לראות ששתי הבעיות שקולות זו לזו בעזרת משפט ארבעת הריבועים של לגראנז' על הצגת מספר טבעי כסכום של ארבעה ריבועים).
האלגוריתם, אם קיים כזה, אמור לקבל משוואה, כדוגמת או , ולקבוע בתוך זמן סופי האם קיים לה פתרון במספרים שלמים.
כשהילברט הציג את הבעיה, ב-1900, הוא ביקש למצוא את האלגוריתם המדובר. הרעיון שייתכן שאין אלגוריתם כזה, ועוד יותר מכך, הרעיון שאפשר להוכיח שהאלגוריתם אינו קיים, היה בלתי נתפס. רק בשנות השלושים של המאה ה-20, לאחר עבודתו של גדל, החלו לשקול ברצינות גם את האפשרות הזו. הניסיונות לפתור את הבעיה הביאו להולדתה של תורת החישוביות, ובסופו של דבר, ב-1970, הוכיח יורי מאטיאשביץ' שהתשובה היא שלילית: האלגוריתם המבוקש אינו קיים.
כמו בכל בעיה אחרת שהציג הילברט, מתמטיקאים רבים עסקו בבעיה זו עד שנפתרה (ונראה שרבים עוד יותר עוסקים ברעיונות שהבעיה הולידה, גם אחרי שנפתרה). עם זאת, במסע לפתרון הבעיה העשירית נקשרו בעיקר ארבעה שמות.
הצעד הראשון: הקשר לחישוביות
ב-1950 כתב מרטין דייוויס את תזת הדוקטורט שלו בהנחייתו של אלונזו צ'רץ', ובה עסק ברעיון של "הצגה דיופנטית" של קבוצה, והעלה את הרעיון שהוביל בסופו של דבר לפתרון הבעיה העשירית של הילברט. הקבוצות שאנו עוסקים בהן כאן הן כולן קבוצות של מספרים טבעיים.
- קבוצה חישובית היא קבוצה שקיים אלגוריתם המכריע לגבי השייכות אליה. כלומר: יש אלגוריתם S שהקלט שלו הוא מספר טבעי, והוא מחזיר - בזמן סופי - את התשובה "כן" או "לא" לגבי ההשתייכות לקבוצה.
- מושג חלש יותר הוא זה של קבוצה הניתנת למנייה חישובית: לקבוצה כזו יש אלגוריתם שיכול לזהות איברים שלה, אבל אין דורשים ממנו תשובה שלילית אם האיבר אינו שייך לקבוצה. האלגוריתם חייב לענות בזמן סופי אם הקלט שייך לקבוצה, אבל עבור קלט שאינו שייך לקבוצה הוא עשוי לרוץ לנצח. מובן שכל קבוצה חישובית היא בפרט ניתנת למנייה חישובית.
- הגדרה אחרת של אותו מושג: 'קבוצה הניתנת למנייה חישובית' היא קבוצה שקיים אלגוריתם שיכול להציג כל אחד מאיבריה בזמן סופי. אין מקום לדרוש שהאלגוריתם יציג בזמן סופי את כל הקבוצה - שהרי זו עשויה להיות קבוצה אינסופית. במקום זה, האלגוריתם צריך לעבור ממספר למספר בקבוצה, כאשר כל צעד נמשך זמן סופי, וב(אינ)סופו של דבר מכסה את הקבוצה כולה.
כבר ב-1936 גילו צ'רץ', אלן טיורינג ואמיל פוסט שקיימות קבוצות הניתנות למנייה חישובית, אבל אינן חישוביות (כלומר, קיים עבורן אלגוריתם המזהה איברים של הקבוצה, אבל לא קיים אלגוריתם שגם מזהה איברים של הקבוצה, וגם מזהה אל-נכון איברים שאינם בקבוצה). קבוצה כזו אפשר לבנות מתוך העובדה שבעיית העצירה למכונות טיורינג אינה ניתנת לחישוב. (ב-1944 העיר פוסט שלבעיה העשירית צריך להיות פתרון שלילי).
דייוויס הציע להתבונן בקבוצות שניתנות ל"הצגה דיופנטית". קבוצה כזו היא קבוצת כל המספרים הטבעיים a שעבורם קיים פתרון למשוואה הדיופנטית הפולינומית . כל פולינום P במקדמים שלמים קובע הצגה דיופנטית של קבוצה: הקבוצה מורכבת מן הרכיב הראשון בכל פתרון של הפולינום P.
ההבחנה החשובה של דייוויס היא שכל קבוצה בעלת הצגה דיופנטית בהכרח גם ניתנת למנייה חישובית (ההוכחה מבוססת על העובדה שהקבוצה בת מנייה). דייוויס העלה את ההשערה שגם הכיוון ההפוך נכון: שלכל קבוצה הניתנת למנייה חישובית, אפשר למצוא הצגה דיופנטית.
נשארה עוד פיסה אחת להשלמת התמונה: האלגוריתם של הילברט, אם קיים כזה, מראה שקבוצה B בעלת הצגה דיופנטית היא תמיד חישובית. אם הקבוצה מוצגת על ידי המשוואה P, האלגוריתם ההיפותטי של הילברט יכול להתבונן במשוואה , ולהכריע - לכל ערך נתון של b - האם יש לה פתרון במשתנים . בכך האלגוריתם מכריע האם b שייך לקבוצה B או לא, ומכאן ש- B חישובית.
סיכום ביניים
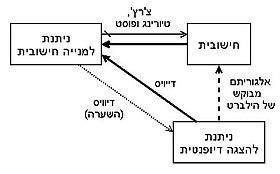
פגשנו שלושה סוגים חשובים של קבוצות: ניתנות להצגה דיופנטית, ניתנות למנייה חישובית, וחישוביות. ברור שכל קבוצה חישובית, ניתנת למנייה חישובית (פשוט משום שזהו תנאי חלש יותר), וגם שכל קבוצה הניתנת להצגה דיופנטית היא ניתנת למנייה חישובית (ההבחנה של דייוויס).
כעת, דייוויס שיער שכל קבוצה ניתנת למנייה חישובית היא גם ניתנת להצגה דיופנטית. האלגוריתם של הילברט מראה במקרה כזה שהקבוצה היא חישובית. אלא שמן הדוגמה של טיורינג ושותפיו אנו יודעים ש"לא כל קבוצה הניתנת למנייה חישובית היא חישובית". אם כך, מן ההשערה של דייוויס נובע שהאלגוריתם שביקש הילברט אינו קיים.
הצעד השני: הצגות דיופנטיות
את המושגים שפגשנו קודם לכן אפשר להכליל לקבוצות של זוגות או שלשות של מספרים. למשל, קבוצת זוגות A ניתנת להצגה דיופנטית אם עבור פולינום P במקדמים שלמים, קיים פתרון למשוואה אם ורק אם הזוג הסדור שייך ל- A. ההכללה הפשוטה הזו מאפשרת לדון בהצגות דיופנטיות של משוואות, במקום קבוצות. אפשר 'לקודד' משוואה כדוגמת בקבוצה , ולומר שהמשוואה ניתנת להצגה (פולינומית) דיופנטית אם ורק אם הקבוצה מקיימת תכונה זו.
נזכיר שדייוויס שיער כי כל קבוצה הניתנת למנייה חישובית, אפשר להציג דיופנטית. ב-1952 תקפה ג'וליה רובינסון את הבעיה 'מלמטה', על ידי בחינה של דוגמאות מוכרות של קבוצות הניתנות למנייה חישובית. בפרט היא ניסתה למצוא הצגות דיופנטיות למשוואות (פונקציית החזקה), (פונקציית העצרת), ולקבוצת המספרים הראשוניים. משימה זו לא צלחה בידה, אולם היא הצליחה להוכיח שניתן יהיה למצוא הצגה דיופנטית לכל המשוואות (או הקבוצות האלה), ברגע שתימצא הצגה דיופנטית ולו לפונקציה אחת הגדלה בקצב מעריכי. לימים הייתה רובינסון, שזכתה במלגת מק'ארתור, המתמטיקאית הראשונה שנבחרה לאקדמיה הלאומית למדעים של ארצות הברית, והנשיאה האישה הראשונה של החברה האמריקאית למתמטיקה.
הצעד השלישי: הצגות דיופנטיות מעריכיות
ב-1962 הראו דייוויס, רובינסון והילרי פטנאם שכל קבוצה הניתנת למנייה חישובית אפשר להציג על ידי פונקציה דיופנטית שהיא 'פולינום מעריכי' (כלומר, הפונקציה מערבת את הפעולות הרגילות של חיבור, חיסור וכפל, אבל גם פעולות העלאה בחזקה). תוצאה זו חלשה יותר מן ההשערה של דייוויס, שבה נדרשת דווקא הצגה על ידי פולינום.
הצעד הרביעי והאחרון: הצגה דיופנטית של משוואות מעריכיות

לאור התוצאות הקודמות של רובינסון, נשאר להציג פונקציה מעריכית אחת. מכאן ייצא שאפשר להציג פולינומית את כל הפונקציות המעריכיות, ובעזרת אלה אנו יודעים כבר שאפשר להציג כל קבוצה הניתנת למנייה חישובית. כך יתקבל אישור להשערת דייוויס, שכל קבוצה הניתנת למנייה חישובית אפשר להציג על ידי פולינום דיופנטי, ואם נציג קבוצה שאינה חישובית נקבל מיד שהאלגוריתם שביקש הילברט לא יכול להתקיים.
המכה בפטיש היה יורי מאטיאשביץ', שהוכיח ב-1972 כי המשוואה ניתנת להצגה דיופנטית פולינומית. כאן הם המספרים בסדרת פיבונאצ'י, שגדלה כידוע בקצב מעריכי. מסקנה: לא קיים אלגוריתם שיכריע בשאלת הפתירות של משוואה דיופנטית.
הכללות
מן העבודה של מאטיאשביץ' נובע כאמור שכל קבוצת מספרים הניתנת למנייה חישובית אפשר להציג באמצעות פולינום דיופנטי. בעבודות אחרות, בעיקר שלו ושל רובינסון, נקבעו חסמים על הגודל של הפולינום הדרוש. כך למשל אפשר תמיד להסתפק בפולינום בתשעה נעלמים (שמעלתו עשויה להמריא עד ל-). מן העבר השני אפשר להסתפק בפולינום ממעלה 4, אלא שאז נדרשים עד 58 נעלמים.
לשאלתו המקורית של הילברט, האם קיים אלגוריתם שיכריע בשאלת קיום פתרון בשלמים למשוואה פולינומית במקדמים שלמים, התשובה היא אם כן שלילית. את אותה שאלה אפשר לשאול גם על חוגים אחרים: בהינתן חוג קומוטטיבי R (עם הצגה אלגוריתמית של תת-קבוצה גדולה מספיק), האם אפשר להכריע בשאלת הקיום של פתרון ב-R למערכת משוואות שמקדמיהן ב-R?
היום ידוע, למשל, שאין אלגוריתם שיכריע לאלו משוואות דיופנטיות יש פתרון מעל:
- חוגי שלמים של שדות גלובליים שיש להם לכל היותר זוג אחד של שיכונים מרוכבים;
- שדות גלובליים ממאפיין חיובי[1] (כגון כאשר שדה סופי).
- שדה הפונקציות הרציונליות במשתנה אחד מעל הממשיים;
- שדה הפונקציות הרציונליות ב- משתנים מעל המרוכבים.
מאידך, קיים אלגוריתם הכרעה לבעיות דומות מעל:
- כל שדה סופי (כמובן);
- שדה המספרים הממשיים ושדה המספרים המרוכבים;
- השדות המקומיים ממאפיין 0.
אלא שזה אינו סוף הסיפור. עדיין לא ידוע אם יש אלגוריתם הכרעה בכמה מקרים חשובים אחרים:
- משוואות עם מקדמים רציונליים (או מכל שדה מספרים אחר);
- משוואות עם מקדמים משדה הפונקציות הרציונליות במשתנה אחד מעל המרוכבים;
- ומשוואות עם מקדמים בשדה מקומי ממאפיין חיובי (היינו ).
לקריאה נוספת
- Bjorn Poonen, Undecidability in Number Theory, Notices of the American Mathematical Society, 55(3), March 2008
- Yuri V. Matiyasevich, Hilbert's Tenth Problem, MIT Press, Cambridge, Massachusetts, 1993
קישורים חיצוניים
- Martin Davis, Reuben Hersh, Hilbert's 10th Problem, Scientific American, 229 (5): 84–91, in JSTOR
- J. P. Jones, Y. V. Matijasevic, Proof of Recursive Unsolvability of Hilbert's Tenth Problem, American Mathematical Monthly, Vol. 98, No. 8 (October 1991), pp. 689-709, in JSTOR
הערות שוליים
- ↑ Alexandra Shlapentokh, Hilbert's Tenth Problem: Diophantine Classes and Extensions to Global Fields
| 23 הבעיות של הילברט | ||
|---|---|---|
| דויד הילברט | ||
| בעיות פתורות (פותרים) | השערת הרצף (גדל, כהן) • הבעיה השנייה של הילברט (גדל, גנצן) • השלישית (דן) • השביעית (גלפונד, שניידר) • העשירית • השלוש-עשרה (ארנולד) • הארבע-עשרה (נגטה) • השבע-עשרה (ארטין) • התשע-עשרה (דה ג'יורג'י, נאש) • העשרים • העשרים ואחת • העשרים ושתיים | |
| בעיות פתורות חלקית (פותרים) | הבעיה הרביעית של הילברט • החמישית (גליסון) • התשיעית (ארטין) • האחת-עשרה (הסה) • החמש-עשרה • השמונה-עשרה | |
| בעיות פתוחות | הבעיה השישית של הילברט • השמינית • השתים עשרה • השש-עשרה • העשרים ושלוש | |
| בעיות המילניום של מכון קליי • בעיות לנדאו | ||
הבעיה העשירית של הילברט37964842Q986147


