מודול שטוח
במתמטיקה, ובמיוחד באלגברה הומולוגית, מודול שטוח מעל חוג הוא מודול מעל , שעבורו פונקטור המכפלה הטנזורית ב- הוא מדויק.
מרחבים וקטורים מעל שדה הם מודולים שטוחים. באופן כללי יותר, מודולים חופשיים, ואף מודולים פרויקטיבים הם מודולים שטוחים. מאידך, כל מודול שטוח הוא חסר פיתול. חוג הוא פון-נוימן רגולרי אם ורק אם כל המודולים מעליו שטוחים (משפט Harada-Auslander), ומושלם (אנ') אם ורק אם כל מודול שטוח הוא פרויקטיבי.
מודולים שטוחים הוגדרו לראשונה על ידי ז'ן-פייר סר (Serre) במאמרו המפורסם "Géometrie Algébrique et Géométrie Analytique", אשר יצא לאור בשנת 1956.
מבוא והגדרה
יהי מודול (שמאלי) מעל החוג . לכל מודול (ימני) אפשר לבנות את המכפלה הטנזורית , שהיא החבורה האבלית הנוצרת על ידי הסמלים הפורמליים (כאשר ), המקיימים כמה חוקים טבעיים. אם , מוגדרת העתקה הרואה כל סמל כאילו הוא חי ב-.
התהליך הזה עלול להיות הרסני: למשל, מעל חוג השלמים , אם , אז המכפלה שווה למודול המנה . אם נתבונן בהכלה , נגלה שהמנה היא חבורה בת איברים, בעוד שהמנה שווה לאפס, כך שאין הכלה . היכולת הזו להרוס הכלות משתקפת במבנה של המודול , ובמקרה זה היא באה לידי ביטוי בכך שהוא מפותל. במקרים אחרים (למשל, אם חופשי) מובטח שהמכפלה הטנזורית ב- תשמור על הכלה. בגלל חשיבותה של התכונה הזו, הציע סר מונח מיוחד למודולים שעבורם
- אם , אז ההעתקה היא שיכון (לכל ולכל ):
מודול המקיים תכונה זו נקרא מודול שטוח.
תכונות יסודיות
כדי שהמודול יהיה שטוח מעל , די בכך שההעתקה היא שיכון לכל שהם אידיאלים שמאליים נוצרים סופית של . כל תת-המודולים של הם שטוחים אם ורק אם כל תת-המודולים הנוצרים סופית הם שטוחים.
הגדרה קטגורית
יהי חוג קומוטטיבי, ויהי מודול מעל . נגדיר פונקטור מהקטגוריה של מודולים מעל לעצמה על ידי .
אפשר להראות כי הפונקטור הוא מדויק מימין. כלומר, בהינתן סדרה מדויקת של -מודולים , הפעלת על הסדרה תיתן סדרה מדויקת . עם זאת, ההעתקה אינה מוכרחה להיות חד חד ערכית.
אם הפונקטור הוא מדויק, נאמר כי הוא -מודול שטוח. לאור הדיון לעיל, הוא שטוח אם ורק אם לכל העתקה חד חד ערכית של -מודולים, ההעתקה המתקבלת על ידי מכפלה טנזורית עם , היא חד-חד-ערכית. מן ההגדרה נובע שמעל חוג חלופי, מכפלה טנזורית של מודולים שטוחים היא שטוחה[1]
במקרה הכללי, כש- אינו בהכרח חילופי, הפונקטור דלעיל עדיין מוגדר על מודולים ומחזיר חבורות אבליות. למרות זאת, ההגדרה נשארת זהה - מודול נקרא שטוח אם הפונקטור כפונקטור מהקטגוריה של -מודולים לקטגוריה של חבורות אבליות הוא פונקטור מדויק.
מתי כל המודולים שטוחים
חוג הוא רגולרי פון-נוימן אם ורק אם כל מודול שמאלי או ימני הוא שטוח, אם ורק אם לכל , המודול הוא שטוח.
כאשר החוג קומוטטיבי, כל המודולים שטוחים אם ורק אם החוג הוא מצומצם (אין בו איברים נילפוטנטיים) וסריג תת-המודולים של כל מודול הוא דיסטריבוטיבי. גם ללא הנחת הקומוטטיביות, אם החוג מצומצם וכל אידיאל חד-צדדי הוא דו-צדדי, אז כל המודולים שטוחים אם ורק אם סריג תת-המודולים של כל מודול הוא דיסטריבוטיבי.
הקשר לפרויקטיביות
כל סכום ישר של מודולים שטוחים הוא שטוח, וכל מחובר ישר במודול שטוח הוא שטוח בעצמו.
כל מודול פרויקטיבי הוא שטוח. בפרט, כל מודול חופשי הוא שטוח. מאידך מודול שטוח עם הצגה סופית הוא פרויקטיבי[2], ולכן עבור מודולים נוצרים סופית מעל חוג נתרי, מודול הוא שטוח אם ורק אם הוא פרויקטיבי. המספרים הרציונליים, כמודול מעל השלמים, הם דוגמה למודול שטוח שאינו פרויקטיבי. אם הוא חוג חילופי נתרי מקומי, אז כל מודול שטוח נוצר סופית מעל הוא מודול חופשי.
מודול שיש לו כיסוי פרויקטיבי (היינו, הוא מנה של מודול פרויקטיבי ביחס לגרעין קטן) הוא שטוח אם ורק אם הוא פרויקטיבי בעצמו. כל המודולים השטוחים מעל חוג הם פרויקטיביים, אם ורק אם החוג מושלם (מחלקה זו כוללת כל תת-חוג (עם יחידה) של חוג פשוט למחצה, וכל מקומי למחצה עם הרמת אידמפוטנטים מ-). התכונה "כל מודול שטוח נוצר סופית הוא פרויקטיבי" חלשה בהרבה; למשל, היא כוללת את כל תחומי השלמות, ואת כל החוגים המקומיים-למחצה הקומוטטיביים (מעל חוג קומוטטיבי, תכונה זו שקולה לכך שכל מודול ציקלי שטוח הוא פרויקטיבי)[3].
אינג'קטיביות
המודול מעל הוא שטוח אם ורק אם אינג'קטיבי מעל . כל מודול שמאלי שטוח הוא אינג'קטיבי אם ורק אם כל מודול ימני שטוח הוא אינג'קטיבי, אם ורק אם החוג ארטיני ואינג'קטיבי.
הקשר לפיתול
כל מודול שטוח הוא חסר פיתול.
מעל חוג השלמים , מודול הוא שטוח אם ורק אם הוא חסר פיתול. לתחום שלמות יש התכונה הזו (שכל מודול חסר פיתול הוא שטוח) אם ורק אם הוא תחום פרופר (היינו תחום שלמות שבו כל האידיאלים הנוצרים סופית הם הפיכים).
מודול שמאלי נקרא חסר-פיתול לפי האטורי (Hattori torsion-free, להלן חפ"ה) אם כל אימת ש- (עבור במודול וסקלר ) אפשר לכתוב כאשר . כל מודול כזה הוא חסר פיתול. את הפיתול לפי האטורי אפשר לאבחן בעזרת אידיאלים ראשיים: מודול הוא חפ"ה, אם ורק אם לכל בחוג, ההעתקה הטבעית היא איזומורפיזם. בפרט, כל מודול שטוח הוא חפ"ה. לכן מחלקת המודולים חסרי הפיתול לפי האטורי היא מחלקת ביניים, הכוללת את כל המודולים השטוחים, ומוכלת בזו של המודולים חסרי הפיתול. מודול הוא שטוח אם ורק אם הוא חפ"ה ומתקיים לכל שני אידיאלים (נוצרים סופית) ימניים .
מעל חוג המקיים את תכונת בזו מימין (כל אידיאל נוצר סופית הוא ראשי), מודול הוא שטוח אם ורק אם הוא חפ"ה; ומעל חוג ללא מחלקי אפס המקיים את תכונת בזו מימין, מודול הוא שטוח אם ורק אם הוא חסר פיתול.
מיקום, גבולות, מכפלות ישרות, פולינומים
מעל חוגים נתריים שטיחות היא תכונה מקומית, כלומר מודול מעל חוג חילופי הוא שטוח אם ורק אם לכל אידיאל ראשוני , המיקום שטוח מעל .
מודול הוא שטוח אם ורק אם הוא מתקבל כגבול ישר של מודולים חופשיים נוצרים סופית. אין בכך מגבלה על גודלו של מודול שטוח, שכן כל מודול הוא גבול ישר של אוסף כל תת-המודולים הנוצרים סופית שלו.
כל מכפלה ישרה של מודולים (שמאליים) שטוחים היא מודול שטוח, אם ורק אם כל מכפלה ישרה של עותקים של החוג היא שטוחה, אם ורק אם החוג הוא קוהרנטי משמאל. כל תת-מודול (שמאלי) של כל מכפלה ישרה של עותקים של החוג הוא שטוח, אם ורק אם כל אידיאל ימני נוצר סופית הוא פרויקטיבי.
יהי חוג קומוטטיבי. חוג המנה (הקומוטטיבי) שטוח כמודול מעל , אם ורק אם האידיאל של הנוצר על ידי המקדמים של הוא מחובר ישר ב-[4].
רזולוציות שטוחות ומכפלה טנזורית נגזרת
בהינתן מודול , רזולוציה שטוחה שלו היא קומפלקס מדויק אשר מורכב ממודולים שטוחים, המרוכז בדרגות שליליות, ביחד עם קוואזיאיזומורפיזם .
בעזרת רזולציות שטוחות ניתן להגדיר את הפונקטור הנגזר משמאל של פונקטור המכפלה הטנזורית: לכל מודול נבחר רזולוציה שטוחה . בהינתן זוג מודולים מעל חוג חילופי , המכפלה הטנזורית הנגזרת שלהם מוגדרת להיות . בניה זו תלויה לכאורה בבחירת הרזולוציה השטוחה, אך ניתן להראות כי בחירת רזולוציה אחרת תוביל לקומפלקס קוואזיאיזומורפי. ההומולוגיות של המכפלה הטנזורית הנגזרת שוות לפונקטור Tor.
קומפלקסים K-שטוחים
ניתן להכליל את מושג המודול השטוח למקרה של קומפלקס שאינו חסום. לכל זוג קומפלקסים ו- מעל חוג , מוגדרת המכפלה הטנזורית . אם הפונקטור הוא מדויק, אומרים כי הוא קומפלקס -שטוח. אם קומפלקס חסום מלמעלה אז הוא -שטוח אם ורק אם כל אחד מהמודולים המרכיבים אותו הוא שטוח. באופן כללי, אם קומפלקס -שטוח כלשהו אז הוא קוואזי-איזומורפי לקומפלקס שכל המודולים המרכיבים אותו הם שטוחים, אך ההפך אינו נכון באופן כללי, כלומר ייתכן שקומפלקס שאינו חסום מלמעלה יהיה מורכב ממודולים שטוחים, אך הקומפלקס לא יהיה -שטוח.
מעל חוג נתון, לכל קומפלקס קיימת רזולוציה -שטוחה, כלומר קיים קומפלקס -שטוח שהוא קוואזי-איזומורפי לו. בעזרת רזולציות אלו אפשר להרחיב את פונקטור המכפלה הטנזורית הנגזרת לכל הקטגוריה הנגזרת של קטגורית המודולים מעל חוג נתון, ללא הגבלת חסימות.
העתקות שטוחות
- הומומורפיזם של חוגים נקרא שטוח אם הוא הופך את למודול חופשי מעל . גרותנדיק הוכיח שכל העתקה חלקה פורמלית בין חוגים נתריים היא שטוחה. בפרט, כל העתקה אטל-פורמלית (Formally étale) (העתקת כיסוי אלגברית) היא שטוחה.
- בפרט, לוקליזציה והשלמה הן העתקות שטוחות.
- הנחת הנתריות הכרחית בהוכחת השטיחות להעתקות חלקות פורמלית. לדוגמה, יהי שדה, ויהי חוג הפולינומים בחזקות רציונליות חיוביות של . ניתן להראות כי ההעתקה השולחת את ל-0 היא העתקה אטל-פורמלית, אך היא אינה העתקה שטוחה. דוגמה זו אינה סותרת את משפטו של גרותנדיק, משום שהחוג איננו חוג נתרי.
הערות שוליים
- ↑ זה מראה שאפילו מעל תחום שלמות, שטיחות היא תכונה יציבה יותר מחוסר-פיתול: מכפלה טנזורית של מודולים שטוחים היא תמיד שטוחה, אבל מכפלה טנזורית של מודולים חסרי פיתול היא חסרת פיתול אם ורק אם D הוא חוג פרופר.
- ↑ D. Lazard, Autour de la platitude, Bull. Soc. Math. France 97 (1969), p.81--128
- ↑ המאמרים [www.mscand.dk/article/download/10979/9000] S. Jondrup, "On Finitely Generated Flat Modules", Math Scand 26 (1970), 233--240 ו-[1] (Puninski-Rothmaler, 2004) עוסקים בשאלה מהן התכונות של חוג שכל מודול נוצר סופית שטוח מעליו הוא פרויקטיבי.
- ↑ M. Nagata: Flatness of an Extension of a Commutative Ring, J. Math Kyoto U, 1969.
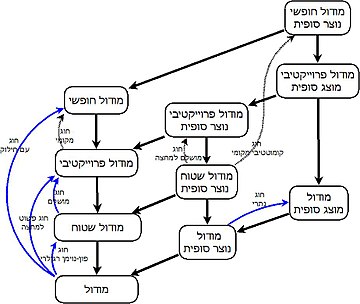
| עץ מיון של מודולים |
|---|
מודול שטוח41372766Q1426191


