פונקציית בסל

במתמטיקה, פונקציית בסל היא פתרון $y(x)$ למשוואה דיפרנציאלית הנקראת משוואת בסל:

$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-p^{2})y=0$

כאשר $p$ קבוע (ממשי או מרוכב) הנקרא הסדר של פונקציית בסל. ברוב המקרים במדע הוא מספר שלם או חצי-שלם.

משוואת בסל מופיעה בתחומים רבים בפיזיקה בהן תופעה בעלת סימטריה גלילית או כדורית מתוארת על ידי משוואה דיפרנציאלית הכוללת את אופרטור הלפלסיאן. בין אלה ניתן למנות את משוואת לפלס באלקטרומגנטיות, משוואת החום המתארת זרימת חום, משוואת שרדינגר במכניקת הקוונטים ותבנית עקיפה בסדק עגול.

פונקציית בסל הוגדרה לראשונה על ידי המתמטיקאי דניאל ברנולי והוכללה על ידי פרידריך בסל.

פונקציית בסל מהסוג הראשון

פונקציות בסל מהסוג הראשון

בפתרון משוואת בסל כטור חזקות (לפי שיטת (טור) פרוביניוס) מתקבלת פונקציית בסל מהסוג הראשון

$J_{p}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{\Gamma (n+1)\Gamma (n+p+1)}}{\left({\frac {x}{2}}\right)}^{2n+p}$

כאשר $p$ , הקבוע במשוואת בסל, הוא דרגת פונקציית בסל ו-$\Gamma (z)$ פונקציית גמא.

פתרון נוסף מתקבל בשיטה זו על ידי החלפת $p$ ב-$-p$ :

$J_{-p}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{\Gamma (n+1)\Gamma (n-p+1)}}{\left({\frac {x}{2}}\right)}^{2n-p}$

אם $p$ איננו שלם, $J_{p}(x),J_{-p}(x)$ הם שני פתרונות בלתי-תלויים למשוואת בסל, שהיא משוואה דיפרנציאלית מסדר שני, ולכן צירוף לינארי שלהם הוא הפתרון הכללי למשוואת בסל. אך כאשר $p$ מספר שלם, ניתן להראות שמתקיים הקשר:

$J_{-p}(x)=(-1)^{p}J_{p}(x)$

במקרה כזה הפתרונות אינם בלתי-תלויים, והפתרון הנוסף הוא פונקציית בסל מהסוג השני.

תכונות פונקציית בסל

• $J_{p}(x=0)=0$ לכל $p$ , למעט $J_{0}(x=0)=1$ .
• עבור p חצי שלם, $\ J_{p}(x)$ ניתנת להבעה באמצעות פונקציות טריגונומטריות. כך, למשל:

$J_{\frac {1}{2}}(x)={\sqrt {\frac {2}{\pi x}}}\sin(x)$

שורשי פונקציית בסל $u_{p,n}$ הנם הנקודות בהן פונקציית בסל מדרגה $p$ מתאפסת. אין נוסחה אנליטית לקבלתם, אך בפיזיקה ובתחומי ההנדסה נוהגים להניח מספר הנחות לגביהם שטרם הוכחו באופן פורמלי:

• שורשי פונקציות בסל אינם מחזוריים.
• עבור $p$ טבעי, לפונקציה יש מספר אינסופי של שורשים.
• לפונקציות בעלות דרגות $p$ שונות אין שורשים משותפים מלבד זה שב-$x=0$ .

יחסי נסיגה:

${\begin{aligned}J_{p-1}(x)+J_{p+1}(x)={\frac {2p}{x}}J_{p}(x)\\J_{p-1}(x)-J_{p+1}(x)=2{\frac {d}{dx}}J_{p}(x)\end{aligned}}$

יחסי אורתוגונליות:

$\int \limits _{0}^{1}xJ_{p}(xu_{p,m})J_{p}(xu_{p,n})dx={\frac {\delta _{m,n}}{2}}[J_{p+1}(u_{p,m})]^{2}={\frac {\delta _{m,n}}{2}}[J_{p}'(u_{p,m})]^{2}$

כאשר $\delta _{m,n}$ הדלתא של קרונקר.

פונקציית בסל מהסוג השני

פונקציית נוימן

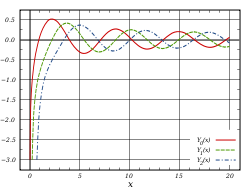
פונקציית בסל מהסוג השני, הנקראת גם פונקציית נוימן או פונקציית וובר, היא פתרון שני של משוואת בסל מדרגה $p$ שהיא מספר לא-שלם, והיא מתבדרת ב-$x=0$ . הפונקציה מסומנת בדרך כלל $N_{p}(x)$ והיא מוגדרת:

$N_{p}(x)={\frac {J_{p}(x)\cos(p\pi )-J_{-p}(x)}{\sin(p\pi )}}$

עבור דרגה $p=n$ שהיא מספר שלם מגדירים את פונקציית בסל מהסוג השני להיות הגבול:

$N_{n}(x)=\lim _{p\to n}N_{p}(x)$

הפתרון הכללי למשוואת בסל מדרגה $p$ יכול אם כן להיכתב בצורה הבאה:

$y_{p}(x)=AJ_{p}(x)+BN_{p}(x)$