התפלגות משולשת

התפלגות משולשת

פונקציית צפיפות ההסתברות
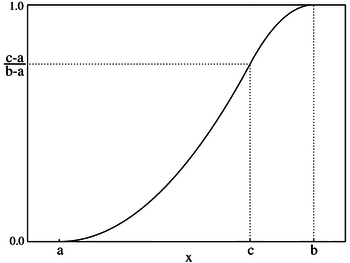
פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים	$a:a\in (-\mathrm{\infty },\mathrm{\infty })$ $b:a<b$ $c:a\le c\le b$
תומך	$a\le x\le b$
פונקציית צפיפות הסתברות (pdf)	$\{\begin{array}{ll}0& \text{for }x<a,\\ \frac{2(x-a)}{(b-a)(c-a)}& \text{for }a\le x<c,\\ \frac{2}{b-a}& \text{for }x=c,\\ \frac{2(b-x)}{(b-a)(b-c)}& \text{for }c<x\le b,\\ 0& \text{for }b<x.\end{array}$
פונקציית ההסתברות המצטברת (cdf)	$\{\begin{array}{ll}0& \text{for }x\le a,\\ \frac{(x-a{)}^2}{(b-a)(c-a)}& \text{for }a<x\le c,\\ 1-\frac{(b-x{)}^2}{(b-a)(b-c)}& \text{for }c<x<b,\\ 1& \text{for }b\le x.\end{array}$
תוחלת	$\frac{a+b+c}{3}$
סטיית תקן	$\sqrt{\alpha }/\lambda$
חציון	$\{\begin{array}{ll}a+\sqrt{\frac{(b-a)(c-a)}{2}}& \text{for }c\ge \frac{a+b}{2},\\ b-\sqrt{\frac{(b-a)(b-c)}{2}}& \text{for }c\le \frac{a+b}{2}.\end{array}$
ערך שכיח	$c$
שונות	$\frac{a^2+b^2+c^2-ab-ac-bc}{18}$
אנטרופיה	$\frac{1}{2}+\ln \left(\frac{b-a}{2}\right)$
פונקציה יוצרת מומנטים (mgf)	$2\frac{(b-c)e^{at}-(b-a)e^{ct}+(c-a)e^{bt}}{(b-a)(c-a)(b-c)t^2}$
צידוד	$\frac{\sqrt{2}(a+b-2c)(2a-b-c)(a-2b+c)}{5(a^2+b^2+c^2-ab-ac-bc{)}^{\frac{3}{2}}}$
גבנוניות	$-\frac{3}{5}$

בהסתברות ובסטטיסטיקה, התפלגות משולשת היא התפלגות רציפה עם גבול תחתון a, גבול עליון b ושכיח c כך ש- a < b ו-a ≤ c ≤ b.

מאפיינים ושימושים

ההתפלגות המשולשת מייצגת התפלגות בסיסית המבוססת רק על חסם עליון, חסם תחתון ושכיח. מהסיבות הללו, יש המכנים אותה "התפלגות של חוסר נתונים". לרוב משתמשים בהתפלגות משולשת כאשר אין מספיק נתונים וההתפלגות אינה אחידה. אולם בעיקר משתמשים בהתפלגות משולשת כאשר היחס בין המשתנים ידוע. בהתפלגות משולשת ניתן גם בקלות לחשב את ההסתברות של קבוצה בתחום, על ידי חישוב השטח שמתחת לעקומה הבנוי ממשולש. בשל מאפיינים אלו, משתמשים לרב בהתפלגות משולשת בסימולציות ובתהליכי קבלת החלטות. משתמשים גם בהתפלגות משולשת בשילוב התפלגות בטא בניהול פרויקטים.

מקרים מיוחדים

קיימים מקרים מיוחדים בהם הנקודות הם ידועות ויש שימוש בערך מסוים של c.

שתי נקודות ידועות

ההתפלגות נהיית יותר פשוטה כאשר a=c או b=c. לדוגמה אם a=0 ו-b=c=1 אז הפונקציית צפיפות ופונקציית הצטברות מוגדרות להיות:

$\begin{array}{ccc}f(x)& =& 2x\\ F(x)& =& x^2\end{array}\}\text{ for }0\le x\le 1$

$\begin{array}{rl}E(X)& =\frac{2}{3}\\ \mathrm{V}\mathrm{a}\mathrm{r}(X)& =\frac{1}{18}\end{array}$

התפלגות של ממוצע שני משתנים עם התפלגות אחידה

כאשר a = 0 b = 1 ו-c = 0.5 שהוא התפלגות של שני משתנים X = (X₁ + X₂)/2, כאשר X₁, X₂ הם שני משתנים אקראיים עם התפלגות אחידה.

$f(x)=\{\begin{array}{ll}4x& \text{for }0\le x<\frac{1}{2}\\ 4-4x& \text{for }\frac{1}{2}\le x\le 1\end{array}$

$F(x)=\{\begin{array}{ll}2x^2& \text{for }0\le x<\frac{1}{2}\\ 2-2(1-x{)}^2& \text{for }\frac{1}{2}\le x\le 1\end{array}$

$\begin{array}{rl}E(X)& =\frac{1}{2}\\ \mathrm{Var}(X)& =\frac{1}{24}\end{array}$

קשר להתפלגות אחידה (המרחק בין שני מ"מ אחידים)

כאשר a = 0, b = 1 ו- c = 0 הוא ההתפלגות של |X = |X₁ − X₂, כאשר X₁, X₂ הם שני משתנים אקראיים עם התפלגות אחידה.

$\begin{array}{rl}f(x)& =2-2x\text{ for }0\le x<1\\ F(x)& =2x-x^2\text{ for }0\le x<1\\ E(X)& =\frac{1}{3}\\ \mathrm{Var}(X)& =\frac{1}{18}\end{array}$

יצירת משתנים אקראיים בעלי התפלגות משולשת

כאשר הינתן משתנה אקראי U שנוצר מהתחום $(0,1)$, על ידי התפלגות אחידה, אז המשתנה

$\begin{array}{c}\{\begin{array}{ll}X=a+\sqrt{U(b-a)(c-a)}& \text{ for }0<U<F(c)\\ & \\ X=b-\sqrt{(1-U)(b-a)(b-c)}& \text{ for }F(c)\le U<1\end{array}\end{array}$

כאשר F(c) = (c-a)/(b-a) הוא בעל התפלגות משולשת עם פרמטרים a, b ו-c.

קישורים חיצוניים

• התפלגות משולשת באתר wolfram mathworld (אנגלית)