טרנספורמציות לורנץ הן טרנספורמציות לינאריות בין מערכות ייחוס המראות כיצד משתנים הזמן והמרחב כאשר עוברים ממערכת ייחוס אחת למערכת ייחוס אינרציאלית הנעה יחסית אליה במהירות קבועה בקו ישר. את טרנספורמציית לורנץ אפשר להסיק מעקרונות היסוד (הפוסטולטים) של תורת היחסות הפרטית, ואכן – טרנספורמציות לורנץ הן כלי מרכזי בביצוע חישובים במסגרת תורה זו.
טרנספורמציית לורנץ פותחה עוד במאה ה-19 בנפרד מתורת היחסות הפרטית על ידי הפיזיקאי ההולנדי הנדריק לורנץ כדי לפתור סתירות שהתגלו בין האלקטרומגנטיות למכניקה הקלאסית. אחת הבעיות הייתה כוח לורנץ המגנטי.
מבוא ודוגמאות
נניח שמערכת ייחוס (צירים + שעון) נמצאת במנוחה ברגע בראשית . נניח שמערכת שנמצאת באותו מקום נעה ביחס אליה במהירות (קבועה) בכיוון .
במכניקה הקלאסית, כדי לחשב כיצד משתנות המדידות של מקום וזמן במערכת לעומת מדידות אלה במערכת משתמשים בטרנספורמציית גליליי:
ברם, כאשר היא מהירות שאינה זניחה יחסית למהירות האור מסתבר שטרנספורמציית גליליי, המתארת כיצד לתרגם מקום וזמן בין שתי המערכות, איננה נותנת תוצאות מדויקות. הטרנספורמציה המתאימה לתרגום ניתנת במסגרת תורת היחסות הפרטית ובניגוד לטרנספורמציית גליליי היא מערבבת בין המרחב והזמן. לטרנספורמציה זו קוראים טרנספורמציית לורנץ או טרנספורמציית לורנץ boost (כאשר boost מרמז כי היא קשורה למהירות) והיא נראית כך:
כאשר פקטור לורנץ ו־ מהירות האור בריק.
אם מסמנים ועובדים ביחידות שבהן ומתעלמים מצירי Y ו־Z שלא משתנים, מקבלים נוסחה פשוטה לזיכרון של הטרנספורמציה:
כאשר הכפל כאן הוא כפל מטריצות רגיל.
| הוכחת הנוסחא לטרנספורמציית לורנץ
|
הנחות היסוד של בפיתוח טרסנפורמציית לורנץ הן
- שקילות של מערכות יחוס אינרציאליות – חוקי הפיזיקה מתקיימים ללא שינוי במערכות אינרציאליות.
- ייחודה של מהירות האור – מהירות האור היא המהירות הגבוהה ביותר שבה ניתן להעביר מידע, והיא זהה בכל המערכות.
נתאר את המרחב-זמן בעזרת תרשים 1, בו מוצגות שלוש נקודות הנמצאות במנוחה יחסית למערכת ייחוס כלשהי. מנקודה B נפלט בזמן t=0 אות אור לעבר נקודת A ו- C. מיקום האות מתואר בעזרת הקווים הכחולים. העובדה שהאות מגיע בדיוק באותו זמן לשתי הנקודות מצוינת על ידי כך שהקו A1, C1 מקביל לציר X (ציר המרחב).
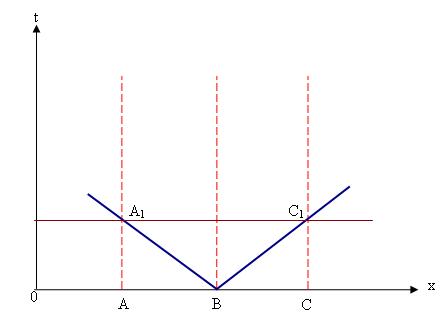
תרשים 1 – תרשים מרחב-זמן. הציר האופקי הוא ציר המרחב, והציר האנכי הוא ציר הזמן. במערכת שלוש נקודות A, B, C, הנמצאות במרחק שווה זו מזו.
הנקודות אינן נעות ביחס למערכת. לכן קו העולם (המקווקו) של כל אחת מהנקודות מקביל לציר הזמן.
נניח עתה כי הנקודות A, B ו- C נעות במהירות קבועה ביחס למערכת S. כלומר, הן נמצאות במנוחה ביחס למערכת 'S, ומערכת זו נעה במהירות קבועה ביחס למערכת S. במערכת S האות אור הנפלט מ- B יגיע קודם אל A ולאחר מכן אל C. תרשים זמן-מרחב של שתי המערכות מופיע בתרשים 2.

תרשים 2 – תרשים מרחב-זמן של האירועים כפי שנצפים במערכת S, כאשר שלוש הנקודות נמצאות במנוחה ביחס למערכת 'S, וזו נעה במהירות קבועה ביחס ל-S. בשתי המערכות הנקודה B נמצאת בדיוק באמצע הקטע AC בזמן t=0.
ההנחה כי מהירות האור שווה בכל מערכות הייחוס מתבטאת בכך שקרני האור, המיוצגות בתרשימים בעזרת הקווים הכחולים, נראות אותו הדבר בדיוק בשתי המערכות. במערכת S, האות לא מגיע ל-'A ול-'C באותו זמן (האירועים אינם סימולטניים). מכאן, שהקו 'A1',C1 אינו מקביל לציר ה-x של מערכת S. מאידך, במערכת 'S שלוש הנקודות נמצאות במנוחה, ולכן במערכת S שני האירועים הם סימולטניים (כלומר, במערכת 'S האור מגיע לנקודות A,C באותו הזמן). מכאן ניתן לתאר את הקואורדינטות של מערכת 'S בהשוואה למערכת S. ציר הזמן 't מקביל לקו העולם של הנקודות ביחס למערכת S, וציר המיקום 'x מקביל לקו הסימולטני 'A1',C1. מערכת הצירים של מערכת 'S מופיעה בתרשים 3.

תרשים 3 – תרשים מרחב-זמן של מערכת S ושל מערכת 'S הנעה במהירות קבועה ביחס ל-S. על סמך קו הסימולטני 'A1',C1.ניתן לקבוע את ציר x' של המערכת הנעה. ציר הזמן t' מקביל לקו העולם של כל אחת מהנקודות A, B, C.
נבחן עתה את תיאורו של אירוע כלשהו P בשתי המערכות. במערכת S האירוע יתואר בעזרת הקואורדינאטות , בעוד שבמערכת 'S יהיה תיאורו בעזרת הקואורדינטות . תיאור האירוע בשתי המערכות S ו- 'S מופיע בתרשים 4.

תרשים 4 – תיאור האירוע P בעזרת שתי מערכות אינרציאליות. מערכת נחה S ומערכת נעה 'S.
מעבר מקואורדינטות של מערכת נחה למערכת נעה
מתרשים 4 ניתן לראות כי ניתן לתאר את הקשרים בין הקואורדינטות של שתי המערכות בעזרת קשרים לינאריים. לכן ניתן לבטא את היחסים בין שתי המערכות בדרך הבאה:
(1)
כאשר מספרים כלשהם, שאותם יש לחשב. אם נבחן את הקוארדינטות במערכת 'S של האירוע (ראשית הצירים של מערכת S), נגלה כי
לפי הגדרה, היחס בין 'x לבין 't הוא מהירות מערכת 'S יחסית ל S, כלומר:
(2)
כאשר v היא מהירות מערכת 'S יחסית ל S.
נעקוב עתה אחרי אות אור היוצא מהראשית 0 ב- t=0. תיאור האות בכל אחת מהמערכות יהיה:
(3)
נציב את משואות (3) במשוואות (1) ונקבל:
(4)
נחלץ את t ו- 't ממשואות (4) ונציב את (2) ונקבל
(5)
ממשוואה זו ניתן לחלץ את a:
(6)
הסימון הסטנדרטי לגודל זה הוא האות היוונית . נציב את (6) ב־(1) ונקבל
וכך קיבלנו את הנוסחא ללטרנספורמצייה של קוארדינטות המרחב. על מנת לקבל את הטרנספורמציה של קואורדינאטות הזמן נציב את (3) ב־(7)
מאחר שאין תנועה יחסית בין מערכת S למערכת 'S בכיוון ציר Y וציר Z, קואורדינטות אלה לא עוברות שינוי, וניתן לסכם את התוצאות בצורה תלת־ממדית:
|
|
הגדרה פורמלית
מרחב מינקובסקי והמטריקה
נגדיר את המטריצה של מרחב מינקובסקי שטוח:
בכתיב טנזורי, רושמים את g כ .
במרחב מינקובסקי הזמן איננו סקלר אלא חלק מ 4-וקטור:
נשים לב כי (כאשר אינדקס מופיע פעם למעלה ופעם למטה, הסכם הסכימה של איינשטיין, קובע שמסכמים על הערכים האפשריים 0,1,2,3) שים לב שזהו לא שוויון מטריציוני ולא מתבצע כפל מטריצות אלא זה שוויון של סכום של איברים. וזהו בעצם חוק שמירות האינטרוול ואינווריאנטיות הזמן העצמי.
חבורת לורנץ
חבורת לורנץ היא החבורה האורתוגונלית של התבנית , כלומר, אוסף המטריצות ההפיכות מסדר 4 על 4, המקיימות , כאשר מסמן את המטריצה המשוחלפת. אלו הן בדיוק הטרנספורמציות הלינאריות של המרחב-זמן השומרות על המטריקה של מינקובסקי.
סיווג טרנספורמציות לורנץ
סיבובים מרחביים
כל טרנספורמציה מהצורה:
כאשר מטריצת סיבוב אורותוגונלית (כלומר: ) היא טרנספורמציית לורנץ. למעשה, זוהי טרנספורמציית סיבוב מרחבית.
המשמעות של זה היא שכל חוקי הפיזיקה ישארו אינווריאנטים גם אם נסובב את מערכת הצירים סביב הראשית, כלומר: לטבע אין כיוון מועדף (איזוטרופיה).
boost
זוהי טרנספורמציה המעבירה ממערכת ייחוס אחת למערכת ייחוס הנעה ביחס אליה במהירות קבועה.
בלי הגבלת הכלליות, נניח שמערכת ייחוס נעה במהירות יחסית בכיוון למערכת ייחוס . אזי כלל התרגום בין 4־וקטור האירוע לבין וקטור האירוע הוא
כאשר פקטור לורנץ ו־c מהירות האור בריק.
את 4 משוואות הטרנספורמציה אפשר לייצג באמצעות מטריצה:
או באופן שקול
כאשר מערכת נעה ביחס ל־ בכיוון כלשהוא, טרנספורמציית לורנץ הכללית תינתן על ידי הרכבה של 2 סיבובים ו־boost. נסובב את שתי המערכות כך שציר X שלהן יהיה באותו כיוון ומקביל לכיוון המהירות היחסית ביניהן, נבצע את ה־boost ואז נסובב בחזרה לקואורדינטות המקוריות. הביטוי הכללי מכוער למדי ואין טעם לרשמו.
חיבור מהירויות יחסותי
כמו כן, מטרנספורמציית לורנץ ה־boost אפשר להסיק כלל של חיבור מהירויות באותו כיוון (על ידי הרכבה של boost על boost) ולקבל כי
שדות אלקטרומגנטיים תחת טרנספורמציית לורנץ
זוהי טרנספורמציה המעבירה את השדה החשמלי ואת השדה המגנטי ממערכת ייחוס אחת למערכת ייחוס הנעה ביחס אליה במהירות קבועה :
- השדה החשמלי במערכת הנעה.
- השדה החשמלי במערכת היחוס.
- השדה המגנטי במערכת הנעה.
- השדה המגנטי במערכת היחוס.
ראו גם
קישורים חיצוניים