אלגוריתם קוונטי

אלגוריתם קוונטי הוא אלגוריתם המיועד לפעול על מחשב קוונטי – מכשיר חישובי המנצל את עקרונות מכניקת הקוונטים, כגון סופרפוזיציה ושזירה קוונטית. אלגוריתמים אלה שונים באופן מהותי מאלגוריתמים קלאסיים, בכך שהם פועלים על קיוביטים במקום על ביטים רגילים, ועושים שימוש בתכונות קוונטיות לביצוע חישובים באופן יעיל יותר עבור בעיות מסוימות.

רקע תאורטי

בעוד מחשבים קלאסיים מבצעים חישובים על סדרות של ביטים הנמצאים באחד משני מצבים (0 או 1), מחשב קוונטי פועל על קיוביטים, שיכולים להימצא בכל סופרפוזיציה של המצבים |0⟩ ו-|1⟩. כאשר מספר קיוביטים מקושרים באמצעות שזירה קוונטית, המערכת כולה יכולה להימצא במצב קוונטי מורכב המייצג בו-זמנית מספר אקספוננציאלי של מצבים.

אלגוריתם קוונטי הוא למעשה סדרת פעולות (שערים קוונטיים) שמבוצעות על קבוצת קיוביטים, ובסיומן מתבצעת מדידה. מטרת האלגוריתם היא לפעול על ההתפלגות ההסתברותית של תוצאות המדידה כך שהתוצאה הרצויה תופיע בהסתברות גבוהה.

יתרונות האלגוריתם הקוונטי

אלגוריתמים קוונטיים מסוגלים, לעיתים, לספק יתרון חישובי מהותי על פני אלגוריתמים קלאסיים. ישנם שני סוגים עיקריים של יתרונות:

• האצה אקספוננציאלית – לדוגמה, אלגוריתם שור לפירוק לגורמים ראשוניים פועל בזמן פולינומי, לעומת האלגוריתמים הקלאסיים הידועים כיום שפועלים בזמן אקספוננציאלי.
• האצה ריבועית – לדוגמה, אלגוריתם גרובר מקצר את זמן החיפוש כאשר מחפשים פריט מסוים בתוך רשימה של $N$ פריטים לא ממויינת מ־$O(N)$ עבור חיפוש קלאסי ל־$O(\sqrt{N})$ באמצעות מחשב קוונטי.

אלגוריתמים בולטים

אלגוריתם דויטש-ג'וזה

מעגל קוונטי המממש את אלגוריתם דויטש-ג'וזה

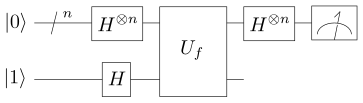
אלגוריתם דויטש-ג'וזה הוא מהאלגוריתמים הקוונטיים הראשונים שהוצגו, ונחשב לדוגמה מובהקת ליתרון קוונטי תאורטי על פני חישוב קלאסי. האלגוריתם עוסק בבעיה הבאה: נתונה פונקציה בוליאנית אשר מובטח מראש שהיא או קבועה (כלומר, מחזירה את אותה התוצאה לכל קלט) או מאוזנת (מחזירה 0 בדיוק למחצית מהקלטים ו-1 למחצית השנייה). המטרה היא לקבוע בוודאות לאיזה סוג משתייכת הפונקציה.

באופן קלאסי, כדי להכריע בוודאות בין שני המקרים יש לבדוק עד מחצית מהקלטים האפשריים בתרחיש הגרוע ביותר – כלומר, $2^{n-1}+1$ קריאות לפונקציה. לעומת זאת, אלגוריתם דויטש–ג'וזה מנצל תכונות קוונטיות כמו סופרפוזיציה והתאבכות קוונטית, ומצליח לקבוע בוודאות את סוג הפונקציה באמצעות קריאה אחת בלבד לאורקל קוונטי.

אף על פי שמדובר בבעיה מלאכותית שלא נחשבת שימושית באופן ישיר, האלגוריתם היווה נקודת מפנה חשובה בתולדות המחשוב הקוונטי, משום שהוא הדגים לראשונה כיצד מחשב קוונטי יכול לפתור בעיה מסוימת במהירות גבוהה לאין שיעור מזו של מחשב קלאסי. כמו כן, רעיונות מתוך האלגוריתם שימשו כבסיס לפיתוח אלגוריתמים קוונטיים חשובים נוספים, כמו אלגוריתם סיימון ואלגוריתם שור.

אלגוריתם ברנשטיין–וזיראני

מעגל קוונטי המממש את אלגוריתם ברנשטיין–וזיראני

אלגוריתם ברנשטיין–וזיראני (Bernstein–Vazirani algorithm) הוא האלגוריתם הקוונטי הראשון שפותר בעיה בצורה יעילה יותר מהאלגוריתם הקלאסי הידוע הטוב ביותר. האלגוריתם הוא גרסה מוגבלת של אלגוריתם דויטש-ג'וזה, והוא נועד לפתור בעיה מקבילה. במקום להפריד בין שתי מחלקות של פונקציות (הפרדה בין פונקציה קבועה לפונקציה שמחזירה בהסתברות שווה 0 או 1), אלגוריתם זה נועד למצוא את מילת הקוד שמגדירה את פונקציית האורקל. האלגוריתם תוכנן על מנת להוכיח כי ניתן להפריד באמצעות אורקל (Separation oracle) בין שתי מחלקות הסיבוכיות BQP ו־BPP.

אלגוריתם סיימון

מעגל קוונטי המממש את אלגוריתם סיימון

האלגוריתם של סיימון פותר בעיית סיימון (Simon's problem) בזמן מהיר יותר באופן מעריכי לעומת כל אלגוריתם קלאסי אחר, כולל אלגוריתמים הסתברותיים עם שגיאה מוגבלת. בעיית סיימון היא בעיית קופסה שחורה שבה הקלט הוא באורך n והפלט באורך m כאשר מתקיים $m\ge n$. אלגוריתם סיימון היווה השראה לאלגוריתם שור לפירוק לגורמים.

אלגוריתם שור

אלגוריתם שור פותר את בעיית הלוגריתם הבדיד (Discrete logarithm) ואת בעיית הפירוק לגורמים (Integer factorization) בזמן פולינומי, בעוד שהאלגוריתמים הקלאסיים הידועים הטובים ביותר דורשים זמן על-פולינומי. לא ידוע האם בעיות אלו הן P (complexity) או NP-completeness. אלגוריתם שור הוא גם אחד מהאלגוריתמים הקוונטים היחידים שפותר בעיה שאיננה בעיית קופסה שחורה בזמן פולינומי, בעת שהאלגוריתמים הקלאסיים הידועים דורשים זמן על-פולינומי.

אלגוריתם הערכת פאזה קוונטית

מעגל קוונטי המממש את אלגוריתם הערכת פאזה קוונטית.

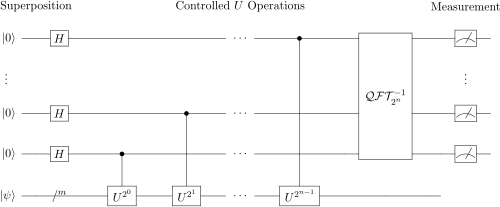
אלגוריתם הערכת פאזה קוונטית (Quantum phase estimation algorithm) משמש לקביעת הפאזה העצמית של וקטור עצמי המתאים לשער אוניטרי מסוים. מציאת הפאזה נעשית באמצעות שימוש במצב קוונטי אשר פרופורציונלי לווקטור העצמי המבוקש וגישה לשער האוניטרי. האלגוריתם משמש לעיתים קרובות כתת-שגרה באלגוריתמים אחרים.

הערכת סכומים גאוסיים

סכום גאוסי (Gauss sum) הוא סוג של סכום מעריכי (Exponential sum). האלגוריתם הקלאסי הידוע הטוב ביותר להערכת סכומים אלו דורש זמן מעריכי. מאחר שבעיית הלוגריתם הבדיד ניתנת לצמצום להערכת סכומים גאוסיים, קיום אלגוריתם קלאסי יעיל להערכת סכומים גאוסיים היה מרמז על קיום אלגוריתם קלאסי יעיל לפתרון בעיית הלוגריתם הבדיד – דבר שנחשב בלתי סביר. עם זאת, מחשבים קוונטים יכולים להעריך סכומים גאוסיים בדיוק פולינומי ובזמן פולינומי באמצעות מגוון שיטות קוונטיות.

דייג פורייה ובדיקת פורייה

דייג פורייה (fourier fishing) ובדיקת פורייה (fourier checking) הן שתי בעיות במחשוב קוונטי הקשורות לתכונות של פונקציה במרחב פורייה. דייג פורייה היא בעיית דגימה, ואילו בדיקת פורייה היא בעיית החלטה. ניתן לתאר בעיות אלו באמצעו אורקל המורכב מ-n פונקציות בוליאניות רנדומליות אשר ממפות כל אחת מחרוזת באורך n לערך בוליאני יחיד. המטרה היא למצוא סט של n מחרוזות $\{z_i{\}}_{i=1}^n$ באורך n מהצורה אשר עבור התמרת אדמר-פורייה (Hadamard transform) מתקיים:

לפחות ¾ מהמחרוזות מקיימות:

$|\tilde{f}(z_i)|\ge 1$

ולפחות ¼ מהמחרוזות מקיימות:

$|\tilde{f}(z_i)|\ge 2$

באמצעות אלגוריתמים קוונטיים הדבר יכול להתבצע בסיבוכיות BQP.

יישומים פוטנציאליים

קריפטוגרפיה

בתחום הקריפטוגרפיה, מאיימים אלגוריתמים קוונטיים על מערכות הצפנה מודרניות, במיוחד אלו הנשענות על קושי פירוק לגורמים, כמו RSA ו־ECC. אלגוריתם שור מסוגל לפרוץ מערכות אלה בזמן פולינומי. בנוסף, אלגוריתם גרובר מקצר את זמן החיפוש במפתחות של הצפנה סימטרית, כמו AES, מ־$O(N)$ ל־$O(\sqrt{N})$, מה שמחייב הארכת מפתחות כדי לשמור על אותה רמת אבטחה. בעקבות איומים אלה, מתפתח תחום קריפטוגרפיה עמידה לקוונטים.

כימיה חישובית

בתחום הכימיה החישובית, מחשבים קוונטיים מתאימים במיוחד לסימולציה של מערכות מולקולריות מורכבות. אלגוריתמים כמו VQE ו־QPE מאפשרים לחשב את אנרגיית היסוד של מולקולות בצורה יעילה. תחום זה עשוי לשנות את הדרך שבה מתכננים תרופות, חומרים מתקדמים וזרזים כימיים. סימולציות אלו כמעט בלתי אפשריות עבור מחשבים קלאסיים משום שמספר המצבים הקוונטיים האפשריים במערכת גדל בקצב אקספוננציאלי ככל שמוסיפים חלקיקים – דבר שדורש כמות עצומה של זיכרון וחישוב.

חיפוש מידע וסטטיסטיקה

כאלגוריתם חיפוש, אלגוריתם גרובר מאפשר ביצוע חיפוש מהיר יותר במידע בלתי ממויין, והוא שימושי בבעיות כמו מציאת פריטים במאגר, פתרון בעיות SAT או בדיקת התנגשויות בפונקציות גיבוב. יתרון זה חשוב בתחומים כמו אבטחת מידע, בקרה, בלוקצ'יין ומחקר סטטיסטי.

ראו גם

• מחשב קוונטי
• קיוביט
• שער קוונטי
• סופרפוזיציה
• שזירה קוונטית
• התמרת פורייה קוונטית
• הצפנה פוסט-קוונטית

קישורים חיצוניים

• Qiskit – ערכת כלים לפיתוח אלגוריתמים קוונטיים
• Quantum AI – פרויקט גוגל
• IBM Quantum

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

אלגוריתם קוונטי41971079Q2623817