חבורת הצמות

חבורת הצמות (Braid group) היא חבורה נחקרת מאוד, בעלת שימושים רבים בתחומים שונים של המתמטיקה, כמו טופולוגיה גאומטרית, גאומטריה אלגברית, הצפנה ועוד. זוהי חבורה אינסופית בעלת הצגה סופית שבמידה מסוימת מכלילה את החבורה הסימטרית הסופית.

הגדרה

לחבורת הצמות מספר הגדרות שקולות, בעלות אופי שוני, המעידות על יישומיה של החבורה בתחומים שונים.

הגדרה אלגברית

בהינתן מספר טבעי n גדול מ-1, חבורת הצמות מסדר $n$ היא החבורה בעלת ההצגה:

$B_{n}=\left\langle \sigma _{1},...,\sigma _{n-1}|{\begin{matrix}\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i},\quad \quad \quad \quad \quad |i-j|\geq 2\\\sigma _{i+1}\sigma _{i}\sigma _{i+1}=\sigma _{i}\sigma _{i+1}\sigma _{i},\quad 1\leq i\leq n-2\end{matrix}}\right\rangle$.

להצגה זו קוראים הצגת ארטין, על שם המתמטיקאי אמיל ארטין שעסק בחבורה והביא הצגה זו לראשונה.

איברי החבורה מכונים צמות. יחסי החבורה נקראים יחסי קומוטטיביות ויחסי הצמות.

הגדרה גאומטרית

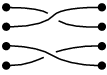
גאומטרית, חבורת הצמות ה-$n$ היא אוסף כל הצמות לאורך $n$ מסלולים (לא מעגליים), יחד עם פעולת הרכבת צמות.

למשל, במקרה $n=4$:

להלן שתי צמות שונות:

$\neq$

ולעומת זאת, זו איננה צמה:

פעולת ההרכבה של צמות נעשית לדוגמה כך:

מורכב על נותן את

מורכב על נותן את

המינוח המדויק נתון במונחים של טופולוגיה אלגברית והומוטופיה, בדומה להגדרה של קשרים. שיקולים שונים מראים כי הצמות בהגדרתן הגאומטרית אכן מקיימות את היחסים כלעיל (עד כדי הומוטופיה). חקר הצמות באופן גאומטרי מכונה תורת הצמות.

הגדרה טופולוגית

את חבורת הצמות ניתן להגדיר בכלים של טופולוגיה אלגברית.

נסמן $D=\{z\mid |z|\leq 1\}$, ותהי $K\subseteq \operatorname {int} D$ קבוצת $n=|K|$ נקודות סופית. נגדיר ב-$B$ את קבוצות הדיפאומורפיזמים $\beta :D\to D$ המקיימות $\beta (K)=K$ (קבוצתית ולא נקודתית), ו-$\beta \mid _{\partial D}=id$.

כעת, על הקבוצה $B$ נגדיר את יחס השקילות הבא: נאמר ש-$\beta \sim \beta '$ אם שניהם משרים את אותו האוטומורפיזם בחבורה היסודית $\pi _{1}(D\setminus K,*)$. נגדיר את חבורת הצמות $B_{n}(D,K)$ להיות חבורת המנה לפי יחס שקילות זה.

כל חבורה $B_{n}(D,K)$ היא בעלת הצגה כלעיל, ובפרט $B_{n}(D',K')\cong B_{n}\cong B_{n}(D,K)$ לכל שני דיסקים ולכל שתי קבוצות נקודות (מאותו גודל).

החבורה $B_{n}(D,K)$ היא מודל טופולוגי של החבורה $B_{n}$. במילים אחרות, הגדרה זו אומרת שחבורת הצמות היא חבורת מחלקות ההעתקות (Mapping class group) של דיסק עם $n$ חורים. זוהי שיטת הסתכלות שימושית העוזרת בהוכחת טענות על חבורת הצמות.

החבורה היסודית של מרחב התצורה

הגדרה נוספת של חבורת הצמות היא בתור החבורה היסודית של מרחב התצורה (Configuration space) של המרחב המרוכב $\mathbb {C} ^{n}$.

נגדיר $F\mathbb {C} ^{n}=\{\left(z_{1},\dots ,z_{n}\right)\in \mathbb {C} ^{n}\mid z_{i}\neq z_{j}\}$ - כלומר, זוהי קבוצה פתוחה במרחב האפיני המרוכב, המהווה משלים של הקבוצה האפינית $\{z_{i}=z_{j}\}$. על קבוצה זו פועלת באופן טבעי החבורה הסימטרית, על ידי החלפת הקורדינאטות, וכך מתקבל המרחב $C\mathbb {C} ^{n}=F\mathbb {C} ^{n}/S_{n}$. העתקת המנה $\tau :F\mathbb {C} ^{n}\to C\mathbb {C} ^{n}$ היא העתקת כיסוי מסדר $n!$.

בהינתן נקודה כלשהי ${\bar {p}}\in F\mathbb {C} ^{n}$, מגדירים את חבורת הצמות הטהורה ה-$n$ להיות $\pi _{1}\left(F\mathbb {C} ^{n},{\bar {p}}\right)$.

המרחב $C\mathbb {C} ^{n}=F\mathbb {C} ^{n}/S_{n}$ הוא מרחב קשיר מסילתית, ועל כן מוגדרת, באי-תלות בנקודת המרכז, החבורה היסודית של המרחב, והיא מוגדרת להיות חבורת הצמות ה-$n$.

מבנה ומקרים פרטיים

יש הומומורפיזם טבעי מחבורת הצמות אל החבורה הסימטרית, המתקבל מכך ש"שוכחים" את המבנה הטופולוגי של הצמות ומתחשבים רק בפעולה שלהן על n הנקודות. הפעולה שולחת את יוצר קוקסטר $\ \sigma _{i}$ אל החילוף $(i,i+1)$ (ההעתקה היא על, משום שהחילופים יוצרים יחד את החבורה הסימטרית). הגרעין של ההעתקה הזו מכונה חבורת הצמות הטהורה ומסומן ${P}_{n}$. כך מוגדרת סדרה מדויקת קצרה $\ 1\longrightarrow P_{n}\longrightarrow B_{n}\longrightarrow S_{n}\longrightarrow 1$.

יש ייצוג של חבורת הצמות עם היוצרים $\ \sigma _{t,s}=\sigma _{s,t}=\sigma _{t-1}\cdots \sigma _{s+1}\sigma _{s}\sigma _{s+1}^{-1}\cdots \sigma _{t-1}^{-1}$ (עבור $\ 1\leq s<t\leq n$), והיחסים $\ \sigma _{st}\sigma _{rs}=\sigma _{rt}\sigma _{st}=\sigma _{rs}\sigma _{rt}$ כאשר $\ 1\leq r<s<t\leq n$, ו-$\ [\sigma _{st},\sigma _{qr}]=1$ כאשר $(t-r)(t-q)(s-r)(s-q)>0$. ייצוג סימטרי זה הוצע על ידי Birman-Ko-Lee.

חבורת הצמות הטהורה נוצרת על ידי האברים $\ A_{ij}=\sigma _{ij}^{2}$ (עבור i<j), המתארים העברה של הפתיל ה-j מתחת לפתילים i+1,...,j-1, ואז מעל ומסביב לפתיל ה-i, ובחזרה מתחת לפתילים הנזכרים לעיל. ידוע ייצוג על ידי יוצרים ויחסים של $\ P_{n}$ במונחי יוצרים אלה. יוצרי חבורת הצמות פועלים על היוצרים $\ A_{ij}$ באופן הבא: $\ \sigma _{i-1}^{-1}A_{ij}\sigma _{i-1}=A_{i-1,j},\ \sigma _{i}^{-1}A_{ij}\sigma _{i}=A_{ij}A_{i+1,j}A_{ij}^{-1},\ \sigma _{j-1}^{-1}A_{ij}\sigma _{j-1}=A_{i,j-1},\ \sigma _{j}^{-1}A_{i,j}\sigma _{j}=A_{j,j+1}A_{i,j+1}A_{j,j+1}^{-1}$, ו-$\ \sigma _{k}^{-1}A_{ij}\sigma _{k}=A_{ij}$ לכל k אחר.

יש אפימורפיזם מ-$P_{n}$ ל-$P_{n-1}$, המתקבל ממחיקת הפתיל ה-n-י (ובמונחי היוצרים, על ידי איפוס היוצרים $\ A_{in}$). הטלה זו מגדירה סדרה מדויקת קצרה $\ 1\longrightarrow \mathbb {F} _{n}\longrightarrow P_{n}\longrightarrow P_{n-1}\longrightarrow 1$, שבה הגרעין הוא חבורה חופשית, הנוצרת על ידי ה-$\ A_{in}$. בפרט, לכל $n>2$ יש ל-$P_{n}$ תת-חבורה חופשית לא אבלית.

• $B_{2}$ נוצרת על ידי איבר אחד ובלי יחסים, ולכן איזומורפית לחבורה הציקלית האינסופית.
• חבורת הצמות היא דוגמה קלאסית לחבורת ארטין, וחבורת קוקסטר המתאימה לה היא החבורה הסימטרית - כלומר, לשתי החבורות אותו מספר יוצרים, אך בחבורה הסימטרית נוספים יחסי השיקוף: $s_{i}^{2}=1$.
• חבורת הצמות היא חבורה חסרת פיתול.

צמות וקשרים

צמות הן במידה מסוימת הכללה של קשרים.

כל צמה ניתן 'לסגור' (ללא קשר נוסף) ולקבל קשר. התאמה זו של צמות אל קשרים היא על - כלומר כל קשר הוא צמה סגורה, אך איננה חח"ע (למשל, צמות צמודות הולכות אל אותו הקשר).

ניתן לעבור בין כל שתי צמות על ידי מספר סופי של צעדי ריידמייסטר. במקרה של שתי צמות שמייצגות אותו הקשר (כולל אוריינטציה), הטענה חזקה יותר - ניתן לעבור בין כל שתי צמות כנ"ל על ידי מספר סופי של צעדים כלהלן: איזוטופיית צמות, יצוב (stabilization) וא-ייצוב (destabilization), המכונים צעדי מרקוב. במקרה של הקשר הטריוויאלי, הטענה עוד יותר טובה - כל צמה המייצגת את הקשר הטריוויאלי ניתן להעביר ליוצר על ידי איזוטופיית צמות, יצוב וצעדי המרה (exchange moves).

ראו את המאמר של בירמן וברנדל לפרטים מלאים.

הצגות

חבורת הצמות היא חבורה לינארית (אינסופית), כלומר ניתן לשכן אותה בחבורת מטריצות מסדר סופי, או במילים אחרות יש לה הצגה לינארית נאמנה.

ההצגות של חבורת הצמות קשורות קשר הדוק באפימורפיזם $\pi :B_{n}\to S_{n}$ - למרות שהגרעין שלו עצום (אינסופי), העתקה זו מאפשרת להרים הצגות של $S_{n}$ (שהמבנה שלהן ידוע בצורה דיי טובה בעזרת דיאגרמות יאנג) להצגות של $B_{n}$.

הצגת בוראו

הצגת בוראו (Burau representation) היא הרמה של ההצגה הנאמנה של $S_{n}$ המתאימה לדיאגרמת יאנג $(n-1)+1$. ההצגה (אותה גילה בוראו באופן בלתי תלוי) $\rho :B_{n}\to GL_{n}(\mathbb {Z} [t,t^{-1}])$ נתונה מפורשות על ידי שליחת היוצרים $\sigma _{i}\mapsto I_{n-i-1}\oplus {\begin{pmatrix}1-t&t\\1&0\end{pmatrix}}\oplus I_{i-1}$. הצגה זו, כמו ההצגה של $S_{n}$ המתאימה לדאיגרמת יאנג $(n-1)+1$, מתפצלת לשתי הצגות, אחת מממד אחד והשנייה מממד $n-1$, המכונה הצגת באראו המצומצמת, ונתונה על ידי ${\bar {\rho }}:B_{n}\to GL_{n}(\mathbb {Z} [t,t^{-1}])$ השולחת יוצרים: $\sigma _{i}\mapsto I_{i-2}\oplus {\begin{pmatrix}1&-t&0\\0&-t&0\\0&-1&1\end{pmatrix}}\oplus I_{n-i-2}$.

הצגת בוראו נאמנה עבור $n\leq 3$, אך איננה נאמנה עבור $n\geq 5$, ולא ידוע האם היא נאמנה עבור $n=4$.

בעזרת הצגת בוראו ניתן לחשב ישירות את פולינום אלכסנדר, שהוא אינווריאנט קשרים: אם $X$ הנה צמה המתאימה אל הקשר $b(X)$, פולינום אלכסנדר שלו הוא $\Delta _{b(X)}(t)={\frac {\operatorname {det} ({\bar {\rho }}(X)-I_{n-1})}{1+t+\dots +t^{n-1}}}$.

בעזרת הצגת בוראו ניתן להכליל את פולינום אלכסנדר לפולינום בשני משתנים - פולינום ה-HOMFLY - שגם הוא אינווריאנט קשרים, וממנו גם ניתן להסיק כמקרה פרטי את פולינום ג'ונס. לפולינום ה-HOMFLY תכונות טובות מאד (לפרטים, ראו במאמר של בירמן וברנדל).

הצגת לורנס-קרמר

ההצגה הבאה שנציג היא הצגה על שמם של המתמטיקאית הישראלית רות לורנס ושל דן קרמר.

לורנס הציגה מספר מונחים כלליים יותר, הצגות לורנס. הצגות לורנס-קרמר הן מקרה פרטי שלה. אלו הן ההעתקות $\lambda _{n}:B_{n}\to GL_{r}(\mathbb {Z} [t,t^{-1},q,q^{-1}])$, אשר מהוות הצגה נאמנה לכל $n$.

בכך הוכח שחבורת הצמות היא חבורה לינארית. לעובדה זה יש שימושים בתחומים שונים, כמו בהצפנה (ראו בהמשך).

צורה נורמלית

אחת ממעלותיה של חבורת הצמות היא שיש לה צורה נורמלית נוחה במיוחד, שגם ניתנת למימוש פשוט במחשב.

צורת גרסייד

הצורה הראשונה שתוצג מכונה צורת גרסייד (Garside normal form).

כדי להגיע לצורה זו, יש ראשית להגדיר את הצמות החיוביות להיות כל הצמות שנוצרות מחזקות חיוביות בלבד של היוצרים. נסמנם ${B}_{n}^{+}$.

אחד הצמות (החיוביות) החשובות היא הצמה היסודית (The fundamental Braid): ${\Delta }_{n}=({\sigma }_{1}{\sigma }_{2}\cdot ...\cdot {\sigma }_{n-1})({\sigma }_{1}{\sigma }_{2}\cdot ...\cdot {\sigma }_{n-2})\cdot ...\cdot {\sigma }_{1}$. איבר זה בריבוע יוצר את המרכז של החבורה, כלומר $Z({B}_{n})=<{{\Delta }_{n}}^{2}>$.

איבר זה מקיים תכונה חשובה, והיא ${\Delta }_{n}{\sigma }_{i}{\Delta }_{n}^{-1}={\sigma }_{n-i}$.

בנוסף, נגדיר צמה פשוטה: עבור יחס הסדר $x\preceq y\Leftrightarrow x=yz,z\in {B}_{n}$ על ${B}_{n}$, נאמר שצמה P היא פשוטה אם $1\preceq P\preceq {\Delta }_{n}$ (כאשר 1 הוא איבר היחידה). יש התאמה בין הצמות הפשוטות לאיבר החבורה הסימטרית (ובפרט כמותם היא $n!$), ולמעשה יותר מכך - איברים אלו הם המקורות הקצרים ביותר של כל איברי $S_{n}$ לפי האפימורפיזם לעיל $\pi :B_{n}\to S_{n}$.

כעת הגענו למשפט ההצגה של גרסייד: כל צמה אפשר להציג ביחידות מהצורה ${{\Delta }_{n}}^{t}{P}_{1}...{P}_{k}$, כאשר t מספר שלם ו${P}_{1},...,{P}_{k}$ צמות פשוטות. צורה זו מכונה הצורה הנורמלית של האיבר. קיים אלגוריתם המוצא את הצורה הנורמלית של צמה נתונה בעל זמן ריצה $O(n^{2}|w|^{2})$, ואלגוריתם טוב יותר ביעילות $O(n\log(n)|w|^{2})$.

על האלגוריתם המפורט להבאת צמה שרירותית לצורה הנ"ל, ראו בקריאה נוספת (D. Garber).

צורת בירמן

צורה נורמלית נוספת (ובמובנים מסוימים אף טובה יותר) היא צורת בירמן, על השם המתמטיקאית ג'ואן בירמן (Joan Birman).

נביט כעת באיבר $\delta _{n}=\sigma _{n-1}\dots \sigma _{1}$. הוא בעל תכונות דומות לצמה היסודית, ומתקיים $\delta _{n}^{n}=\Delta _{n}^{2}$.

צורת בירמן של צמה כללית היא הצגה יחידה בצורה $\delta _{n}^{k}A_{1}\dots A_{t}$, כאשר $A_{i}$, המכונים גורמים קנוניים (Cannoical factors), ידועים מראש, כפונקציה של $P_{i}$ מהסעיף הקודם.

היתרון בצורה זו הוא שכמות הגורמים הקנוניים היא כמספר קטלן: $C_{n}={\frac {(2n)!}{n!(n+1)!}}$ ששווה אסימפטוטית ל-$\sim {\frac {4^{n}}{n^{1.5}}}$. יותר מכך, יש אלגוריתם יותר יעיל למציאת צורה זו, ביעילות $O(n|w|^{2})$.

חבורת הצמות והצפנה

חבורת הצמות היא אחד המועמדים הטבעיים והטובים ביותר בפרוטוקולי הצפנה שונים בהצפנה לא קומוטטיבית.

הצגתה הנוחה שהוצגה לעיל, כמו גם העובדה שהיא לינארית, מאפשרות לממש ייצוג במחשב שבעזרתו ובעזרת תכונות החבורה אפשר להכפיל ולהשוות את האיברים בצורה יעילה. בנוסף, לחבורה בעיית חיפוש מצמיד קשה במיוחד, מה שפותח את הדלת לשימוש בפרוטוקולים רבים, כמו Ko, Lee, et. al או Anshel-Anshel-Goldfeld.

תת-החבורות (שצריכות להתחלף ביניהן) שאפשר לבחור בפרוטוקולים כלעיל הן $A=\langle {\sigma }_{1},...,{\sigma }_{n/2-1}\rangle ,\quad B=\langle {\sigma }_{n/2+1},...,{\sigma }_{n-1}\rangle$. על פי אחת ההמלצות המקובלות, יש להשתמש בפרוטוקולים כמו הנ"ל בחבורת הצמות מסדר 80 ובתת חבורות עם 12 יוצרים לפחות.

חבורת הצמות האינסופית

מתוך ההגדרה לעיל, ניתן להגדיר את חבורת הצמות האינסופית. את חבורת הצמות מסדר n ניתן לשכן באופן טבעי בחבורת הצמות מסדר n+1, כלומר אפשר לומר כי ${B}_{n}\subseteq {B}_{n+1}$. אם כן, חבורת הצמות האינסופית מוגדרת בתור הקו-גבול: ${B}_{\infty }=\lim _{n\rightarrow \infty }{{B}_{n}}$; הלכה למעשה, ניתן לחשוב על כך כעל האיחוד על פני השרשרת ${B}_{2}\subset {B}_{3}\subset \cdots$. הצגה אינסופית שלה היא ${B}_{\infty }=\langle {\sigma }_{1},{\sigma }_{2},...\mid {\sigma }_{i}{\sigma }_{j}={\sigma }_{j}{\sigma }_{i},{\sigma }_{i+1}{\sigma }_{i}{\sigma }_{i+1}={\sigma }_{i}{\sigma }_{i+1}{\sigma }_{i}\rangle$.

על חבורה זו ניתן להגדיר טופולוגיה כך שתהיה חבורת מחלקות ההעתקות של דיסק עם מספר בן מנייה של חורים.

חבורת הצמות הטהורה האינסופית איזומורפית לחבורה היסודית של קוביית הילברט (Hilbert Cube) $[0,1]^{\mathbb {N} }$ פחות האיברים מהצורה $\{(x_{i}):\exists i\neq j:x_{i}=x_{j}\}$.

לקריאה נוספת

• סיכום נרחב על חבורת הצמות: J. Briman, T. Brendle; Braids: A Survey
• על תכונות של חבורת הצמות והקשר להצפנה:
  • Braid Group Cryptography, David Garber,April 16, 2009, World Scientific
  • An Overview Of Braid Group Cryptography, Karl Mahlbrug