פונקציות זוגיות ואי-זוגיות
פונקציות זוגיות ואי-זוגיות הן פונקציות ממשיות בעלות סימטריה מוגדרת ביחס לישר (כלומר לציר ה-).
מקור השם
המונח "פונקציה זוגית" נטבע על ידי לאונרד אוילר, ומופיע לראשונה בספרו שיצא ב-1727,[1] והשימוש הראשון הידוע במונח "פונקציה אי-זוגית" הוא בספר של תומאס לייבורן שיצא ב-1814.[2] הסברה המקובלת היא שהכינויים "זוגי" ו"אי-זוגי" נובעים מהעובדה שהפונקציה היא פונקציה זוגית כאשר זוגי ופונקציה אי-זוגית כאשר אי-זוגי.[3][4]
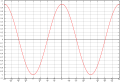
פונקציה זוגית
הגדרה: ערכה זהה עבור כל מספר בתחום ההגדרה ועבור המספר הנגדי לו, כלומר .
סימטריה: כל פונקציה זוגית היא סימטרית ביחס לציר ה-.
דוגמאות של פונקציות זוגיות:
-
פרבולה בעלת קודקוד בנקודה (0,0)
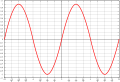
פונקציה אי-זוגית
הגדרה: ערכה עבור כל מספר בתחום ההגדרה הוא המספר הנגדי של ערכה עבור המספר הנגדי לו, כלומר .
סימטריה: כל פונקציה אי-זוגית היא אנטי-סימטרית ביחס לציר ה- (כלומר יש לה סימטריית סיבוב של סביב לראשית).
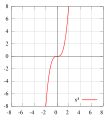
דוגמאות של פונקציות אי-זוגיות:
-
פונקציה ליניארית שעוברת דרך הנקודה (0,0)
פונקציה כללית
ניתן לייצג כל פונקציה באמצעות סכום של פונקציה זוגית ואי זוגית:
- וזאת כאשר: ו
יצוג זה הוא יחיד. מכאן נובע שמרחב הפונקציות כולן מהווה סכום ישר של מרחבי הפונקציות הזוגיות והאי-זוגיות (כשחיבור וכפל בסקלר מוגדרים נקודתית).
לפעמים, עבור פונקציות מרוכבות, הפונקציה הזוגיות והאי זוגית מיוצגים בהתאמה באופן הבא:
ו-
או:
ו-
בצורת כתיבה זאת ניתן להוכיח בקלות רבה תכונות של התמרת פורייה.
תכונות
- סכום פונקציות:
- סכום של פונקציות זוגיות הוא פונקציה זוגית (בפרט, בפתוח של פונקציה אנליטית זוגית לטור טיילור יופיעו רק חזקות זוגיות ובפתוח של פונקציה זוגית מ- לטור פורייה יופיעו רק איברי הקוסינוס).
- סכום של פונקציות אי-זוגיות הוא פונקציה אי-זוגית (בפרט, בפתוח של פונקציה אנליטית אי-זוגית לטור טיילור יופיעו רק חזקות אי-זוגיות ובפתוח של פונקציה אי-זוגית מ- לטור פורייה יופיעו רק איברי הסינוס).
- מכפלת פונקציות:
- מכפלה של פונקציה זוגית בפונקציה זוגית היא פונקציה זוגית.
- מכפלה של פונקציה אי-זוגית בפונקציה אי-זוגית היא פונקציה זוגית.
- מכפלה של פונקציה זוגית בפונקציה אי-זוגית היא פונקציה אי-זוגית.
- חלוקת פונקציות:
- מנה של פונקציה זוגית בפונקציה זוגית היא פונקציה זוגית.
- מנה של פונקציה אי-זוגית בפונקציה אי-זוגית היא פונקציה זוגית.
- מנה של פונקציה זוגית בפונקציה אי-זוגית היא פונקציה אי-זוגית.
באופן כללי כל מכפלה הכוללת פונקציות זוגיות ולא זוגיות בלבד (הפונקציה היא לא זוגית), הפונקציות הזוגיות משמרות את הזוגיות, והזוגיות תלויה האם מספר הפונקציות האי זוגיות זוגי או לא זוגי.
- הרכבת פונקציות:
- הרכבה הכוללת פונקציות זוגיות ולא כוללת פונקציות כלליות היא פונקציה זוגית.
- הרכבה של פונקציות אי-זוגיות היא פונקציה אי-זוגית.
- הרכבה של כל פונקציה עם פונקציה זוגית היא זוגית, אך הרכבה של פונקציה זוגית על פונקציה כללית אינה בהכרח זוגית.
- גזירת פונקציה:
- נגזרת של פונקציה זוגית היא פונקציה אי-זוגית (אם אינה אפס).
- נגזרת של פונקציה אי-זוגית היא פונקציה זוגית.
- נגזרת של פונקציה כללית היא פונקציה כללית או זוגית.
הוכחה:הגדרת הנגזרת בנקודה , היא הגבול .
ניתן להגדיר את כ- ואת כ-
כעת נציב בגבול: . נראה שאם נחליף את הסימן של ושל נקבל לפונקציה זוגית, כלומר שסימן הגבול התחלף. ולפונקציה אי זוגית נקבל, כלומר שסימן הגבול נשמר.
- אינטגרל של פונקציה:
- כל פונקציה קדומה של פונקציה אי-זוגית היא פונקציה זוגית.
- לפונקציה זוגית יש פונקציה קדומה אחת שהיא אי-זוגית - הפונקציה שבה המקדם החופשי שווה ל-0. שאר הפונקציות הקדומות הן כלליות.
- האינטגרל המסוים של פונקציה אי-זוגית בתחום סימטרי שווה לאפס.
- האינטגרל המסוים של פונקציה זוגית בתחום סימטרי שווה לפעמיים האינטגרל בחצי התחום הסימטרי.
- תכונת האפס: כל פונקציה אי זוגית המוגדרת ורציפה בנקודה חייבת לקיים .
קישורים חיצוניים
הערות שוליים
- ↑ Earliest Known Uses of Some of the Words of Mathematics – "ראשית יש לציין את אותן פונקציות, שאני קורא להן זוגיות, שיש להן התכונה שהן אינן משתנות כאשר במקום x מציבים -x".
- ↑ Earliest Known Uses of Some of the Words of Mathematics,
Thomas Leybourn, New Series of The Mathematical Repository, Volume 3, עמוד 61 (קריאת הספר בתצוגה מלאה באתר "גוגל ספרים" )
)
- ↑ Even and Odd Functions and Function Symmetry, באתר ck-12.org
- ↑ Even and Odd Functions, באתר Tree of Math
פונקציות זוגיות ואי-זוגיות37732588Q126592