התפלגות נורמלית

התפלגות נורמלית

פונקציית צפיפות ההסתברות
פונקציית ההסתברות המצטברת
שגיאה ביצירת תמונה ממוזערת:
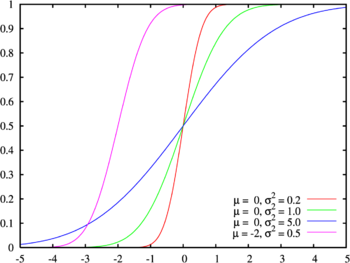מאפיינים
פרמטרים	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mu} התוחלת, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sigma} סטיית התקן.
תומך	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Bbb{R}}
פונקציית צפיפות הסתברות (pdf)	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!}
פונקציית ההסתברות המצטברת (cdf)	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac12 \left(1 + \mathrm{erf}\,\frac{x-\mu}{\sigma\sqrt2}\right) \!}
תוחלת	$\ \mu$
סטיית תקן	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sigma}
חציון	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mu}
ערך שכיח	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mu}
שונות	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sigma ^2}
אנטרופיה	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!}
פונקציה יוצרת מומנטים (mgf)	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right)}
פונקציה אופיינית	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_X(t)= \exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)}
צידוד	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 0}
גבנוניות	$\ 0$

התפלגות נורמלית היא התפלגות חשובה ביותר בסטטיסטיקה תאורטית וביישומיה בכל תחומי המדע. חשיבותה הרבה נובעת ממשפט הגבול המרכזי, לפיו הממוצע של משתנים בלתי תלויים בעלי אותה התפלגות, לאחר תקנון מתאים, מתכנס בהתפלגות אל ההתפלגות הנורמלית. לכן מופיעה התפלגות זו בכל מקום בו לוקחים ממוצע של משתנים רבים, כגון גובה ממוצע של אנשים באוכלוסייה, ממוצע טעויות מדידה מקריות במדידות חוזרות של אותו גודל, וכדומה. מדדים פסיכומטריים שונים, כגון מבחן מנת משכל, מתוכננים בכוונה תחילה להתפלג באופן נורמלי.

ההתפלגות הנורמלית הסטנדרטית (קרויה גם התפלגות Z) היא השימושית ביותר במשפחת ההתפלגויות הנורמליות. על ידי מתיחה (כלומר, הכפלה בקבוע) והזזה (הוספת קבוע) של משתנה מקרי בעל התפלגות נורמלית סטנדרטית, מתקבלת משפחה כללית יותר של התפלגויות, שכל אחת מהן היא התפלגות נורמלית. זוהי דוגמה למשפחה מעריכית של התפלגויות. בתוך המשפחה, אפשר לזהות התפלגות נורמלית מסוימת על-פי שני פרמטרים: התוחלת והשונות שלה. להתפלגות הנורמלית הסטנדרטית יש תוחלת 0, ושונותה 1.

ההתפלגות הנורמלית נקראת גם גאוסיאן על שמו של קרל פרידריך גאוס, וגם עקומת הפעמון משום שהגרף של פונקציית הצפיפות שלה מזכיר בצורתו פעמון.

היסטוריה

המתמטיקאי אברהם דה מואבר הציג את ההתפלגות הנורמלית לראשונה בשנת 1733 כקירוב להתפלגות הבינומית עבור מספר גדול של דגימות (מאמרו בעניין התגלה רק ב-1924). לפלס השתמש בעקומה הנורמלית לתאר "התפלגות של שגיאות" בשנת 1783. גאוס השתמש בהתפלגות הנורמלית לניתוח מידע אסטרונומי ב-1809. המדען הבלגי אדולף קטלה הראה כי התפלגותם של משתנים רבים (כגון גובהו של אדם) היא נורמלית.

מאפיינים מתמטיים

פונקציית הצפיפות

פונקציית הצפיפות של התפלגות נורמלית בעלת תוחלת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} ושונות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2} היא :

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f(x) & = \frac 1 {\sqrt{2\pi\sigma^2}} e^{\frac{-(x-\mu)^2}{2\sigma^2}} \\ & = \frac 1 {\sigma\sqrt{2\pi}} \exp \left( {\frac{-(x-\mu)^2}{2\sigma^2}} \right) \end{align} }

זוהי פונקציה סימטרית סביב התוחלת, ובעלת שתי נקודות פיתול במרחק סטיית תקן אחת מן הממוצע, כלומר בנקודות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mu \pm \sigma} . את העובדה שמשתנה מקרי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ X} הוא בעל התפלגות כזו, מקובל לציין בסימון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle X \sim N(\mu,\sigma^2)} .

במקרה המיוחד של ההתפלגות הנורמלית הסטנדרטית $X\sim N(0,1)$, מתקבלת הפונקציה

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} }

פונקציית ההתפלגות המצטברת

פונקציית ההתפלגות המצטברת, או הסיכוי שמשתנה מקרי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ X} יקבל ערך קטן או שווה ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ x} נתון, שווה ל-

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(X \leq x) = \int_{-\infty}^xf(y)dy}

כדי לחשב את ערכי פונקציית ההתפלגות המצטברת בעלת פרמטרים $\ (\mu ,\sigma ^{2})$ כלשהם, די בידיעת ערכיה של פונקציית ההתפלגות המצטברת הסטנדרטית, משום שאם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ X\sim N(\mu,\sigma^2)} ניתן להגדיר משתנה מקרי חדש הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ Z=\frac{X-\mu}{\sigma}} ולגביו יתקיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ Z\sim N(0,1)} . לכן, מתקיים:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ P(X\le x)=P\left(\frac{X-\mu}{\sigma}\le\frac{x-\mu}{\sigma}\right)=\Phi\left(\frac{x-\mu}{\sigma}\right)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Phi(x)} - מסמל את פונקציית ההתפלגות המצטברת של משתנה נורמלי סטנדרטי.

בשל תכונות הסימטריה של ההתפלגות הנורמלית, בדרך כלל לא נתונים ערכיה השליליים של ההתפלגות הסטנדרטית בטבלאות המשמשות למציאתה. כדי למצוא אותם משתמשים בזהות: $\ \Phi (-x)=1-\Phi (x)$.

הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \Phi(x)} איננה פונקציה אלמנטרית (כלומר, היא אינה מתקבלת מהרכבה סופית של פולינומים, פונקציית האקספוננט והפונקציות הטריגונומטריות, והפונקציות ההפוכות להם). משום כך, כמעט כל ספר העוסק במבחנים סטטיסטיים כולל גם טבלה המכילה את הערכים המקורבים להתפלגות הנורמלית הסטנדרטית, שחושבו בשיטות נומריות. הקירוב הבא שימושי למדי כאשר z גדול:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 1-\Phi(z) = \int_{z}^{\infty} \frac{1}{\sqrt{2\pi}}e^{-x^2/2} dx \approx \frac{1}{z+1/2}e^{-z^2/2} }

תכונות ההתפלגות

שגיאה ביצירת תמונה ממוזערת:

חלוקה של ההתפלגות הנורמלית לפי רבעונים, אחוזונים וסטיות תקן

• ההתפלגות מתפרשת על פני כל הישר הממשי.
• ההתפלגות היא סימטרית וחד שיאית (יונימודלית).
• הממוצע, החציון והשכיח מתלכדים בציר הסימטריה.
• אם נתון משתנה מקרי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle X \sim N(\mu, \sigma^2)} ו- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ a, b} מספרים ממשיים, אזי: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle aX + b \sim N(a\mu+b,\, a^2\sigma^2)} .
• אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle X \sim N(\mu_X, \sigma^2_X)} ו- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y \sim N(\mu_Y, \sigma^2_Y)} משתנים מקריים, בלתי תלויים, אז סכומם מתפלג נורמלית עם הפרמטרים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = X + Y \sim N(\mu_X + \mu_Y, \sigma^2_X + \sigma^2_Y)} או הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = X - Y \sim N(\mu_X - \mu_Y, \sigma^2_X + \sigma^2_Y)} .
• אם X,Y משתנים נורמליים סטנדרטיים ובלתי תלויים, אז הצירופים הליניאריים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ aX+bY, cX+dY} בלתי-תלויים אם ורק אם וקטורי המקדמים מאונכים, כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ ac+bd=0} .
• פיזור ערכי ההתפלגות: 68.26% מן הערכים נמצאים במרחק של לא יותר מציון תקן אחד מהממוצע (ציר הסימטריה). במרחק של עד שני ציוני תקן (z=2) נמצאים 95.44% מהערכים ובמרחק עד שלושה ציוני תקן נמצאים 99.74% מהערכים - רק ב-0.26% יהיה ציון התקן גבוה מ-3.
• גרף ההתפלגות נודע גם בשם "גרף פעמון" או "פעמון גאוס", שכן כאשר הוא משורטט בתור גרף המציין את מספר הערכים בכל תחום, מקבלת העקומה צורה דמוית פעמון - גבוהה במרכזה ונמוכה בשני צדדיה. צורת הפעמון מוכתבת על ידי הממוצע וסטיית התקן של ההתפלגות.

אחוזי ההתפלגות הנורמלית מסביב לממוצע (ציר הסימטריה) לפי סטיות תקן

סימולציה של משתנים המתפלגים נורמלית

הצורך ליצור נתונים שהתפלגותם היא בקירוב התפלגות נורמלית עולה בתחומים רבים. בשפות תכנות רבות קיים מחולל פסבדו אקראי המייצר משתנים המתפלגים, בקירוב, התפלגות אחידה על הקטע $\ [0,1]$, ולכן דרושה שיטה להפוך את המשתנה המקרי האחיד למשתנה המתפלג התפלגות נורמלית סטנדרטית. ישנן מספר דרכים לעשות זאת:

"לאורך כל הדוגמאות המובאות בפסקה זו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ X} יסמן משתנה מקרי המתפלג אחיד על קטע היחידה."

• דרך אינטואיטיבית (אך לא יעילה) ליצור משתנה מקרי המתפלג נורמלית בקירוב היא על ידי שימוש במשפט הגבול המרכזי הקובע כי סכום של מספר גדול של משתנים מקריים אחידים שואף להתפלגות נורמלית. על מנת ליצור התפלגות נורמלית סטנדרטית יש לדאוג שתוחלת הסכום תהיה שווה לאפס וסטיית התקן לאחת. לכן, המשתנה המקרי

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y=\sqrt\frac{12}{N}\left(X_1+X_2+\dots+X_N-\frac{N}{2}\right)}

מתפלג בקירוב התפלגות נורמלית סטנדרטית, וככל שמספר המחוברים גדל, כך גדל הדיוק.

• שיטה כללית יותר, ומדויקת מבחינה מתמטית מתקבלת על ידי הפיכת פונקציית ההסתברות המצטברת. באופן כללי, אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ F} היא פונקציית ההסתברות המצטברת של התפלגות נתונה, אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ F^{-1}(X)} מתפלג בהתפלגות זו. לכן,

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ Y=\mbox{erf}^{-1}(2X-1)}

מתפלג נורמלית, כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{erf}} היא פונקציית השגיאה. על מנת להשתמש בשיטה זו יש לדעת לחשב את פונקציית השגיאה, שהיא אינה פונקציה אלמנטרית.

• שיטה יעילה יותר שגם היא מדויקת מבחינה מתמטית נקראת טרנספורמציית בוקס-מולר. טרנספורמציה זו משתמשת בעובדה שהתפלגות כי בריבוע עם שתי דרגות חופש היא התפלגות מעריכית, וקיימת נוסחה מדויקת להפיכת משתנה מקרי אחיד למשתנה המתפלג מעריכית. טרנספורמציית בוקס-מולר לוקחת שני משתנים מקריים אחידים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ X_1, X_2} ומחזירה שני משתנים מקריים בלתי תלויים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ Y_1 ,Y_2} המתפלגים נורמלית על ידי הנוסחה

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}Y_1 &=& \sqrt{- 2 \ln X_1} \, \cos(2 \pi X_2)\\Y_2 &=& \sqrt{- 2 \ln X_1} \, \sin(2 \pi X_2) \end{align}}

מבחני נורמליות

מבחני נורמליות מעריכים את הסבירות שאוסף נתונים {x₁, …, x_n} מגיע מהתפלגות נורמלית. בדרך כלל השערת האפס H₀ היא שהתצפיות מתפלגות נורמלית עם ממוצע כלשהו μ ושונות σ², מול ההשערה החלופית H_a שההתפלגות היא שרירותית. מבחנים רבים (מעל 40) הומצאו לבעיה זו, להלן הבולטים שבהם:

• בדיקות חזותיות יותר מושכות מבחינה אינטואיטיבית, אבל בו בזמן הן סובייקטיביות מכיוון שנסמכות על שיפוט אנושי בלתי פורמלי על מנת לקבל או לדחות את השערת האפס.
  • תרשים צפיפות אמפירי - בדיקת ההיסטוגרמה או תרשים הצפיפות לראות האם התפלגות נראית נורמלית.
  • תרשים Q-Q של הערכים הממוינים של אוסף הנתונים כנגד הערכים הצפויים של השברונים המתאימים מההתפלגות הנורמלית הסטנדרטית. זהו תרשים של נקודות מהצורה (Φ⁻¹(p_k), x_(k)) כאשר p_k = (k − α)/(n + 1 − 2α) ו-α הוא קבוע ההתאמה, שיכול לקבל כל ערך בין 0 ל-1. אם השערת האפס נכונה, נקודות התרשים אמורות להיות בערך על הקו הישר.
  • תרשים P-P דומה לתרשים ה Q-Q אבל בשימוש נדיר הרבה יותר. בשיטה זו מייצגים בתרשים את הנקודות (Φ(z_(k)), p_k) כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle z_{(k)} = (x_{(k)}-\hat\mu)/\hat\sigma} . בשביל הנתונים המתפלגים נורמלית, תרשים זה אמור להיות בערך על הקו הליניארי שבין (0,0) ובין (1,1).
  • מבחן שפירו-ווילק משתמש בעובדה שלקו בתרשים Q-Q יש שיפוע σ. המבחן משווה את הערכת הריבועים הפחותים של השיפוע עם ערך השונות המדגמית, ודוחה את השערת האפס אם שני הערכים האלה שונים משמעותית.
• מבחני מומנט
  • מבחן K-ריבועי של ד'אגוסטינו
  • מבחן ז'רקה- ברה.
• מבחני פונקציית התפלגות אמפירית
  • מבחן ליליאפורס (אדפטציה של מבחן קולמוגורוב-סמירנוב).
  • מבחן אנדרסון-דרלינג

התפלגות רב-נורמלית

ערך מורחב – התפלגות רב-נורמלית

ההכללה הנכונה של התפלגות נורמלית לווקטור משתנים מקריים היא זאת: אומרים ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{X} = (X_1,\dots,X_n)} מתפלג רב-נורמלית (או גאוסיאנית) אם כל צירוף ליניארי שלו מתפלג נורמלית (חד-ממדי), כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \bar{A}, \bar{X}\rangle = a_1X_1 +\dots +a_nX_n \sim N(\mu,\sigma^2)} . זה קורה אם ורק אם הפונקציה האופיינית של המשתנה היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi_X(\bar{a}) = e^{i\langle \bar{\mu},\bar{a} \rangle - \frac{1}{2}\bar{a} V \bar{a}^t}} , כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} היא מטריצת השונויות המשותפות. היות שהמטריצה הזו סימטרית, אפשר ללכסן אותה אורתוגונלית. המטריצה האלכסונית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} המתקבלת קובעת את סינגולריות המשתנה - אומרים שהוא רגולרי אם ורק אם אין ערכים עצמיים לא אפס, והיותו של המשתנה רגולרי שקולה לכך שיש לו פונקציית צפיפות (ביחס למידת לבג).

למשתנים מקריים רב-נורמליים מספר יישומים בתורת ההסתברות וסטטיסטיקה, כמו בקביעת התפלגות של ממוצע וסטיית תקן של מדגם נרחב של משתנים מקריים נורמליים.

ראו גם

• משפט הגבול המרכזי
• אינטגרל גאוסיאני
• התפלגות רב-נורמלית
• התפלגות תת-גאוסית

קישורים חיצוניים

• מחשבון ערכי התפלגות נורמלית
• ארז גרטי, התפלגות נורמלית, באתר של מכון דוידסון לחינוך מדעי, 5 בנובמבר 2011
• מחשבון התפלגות נורמלית סטנדרטית בעברית
• יוסי לוי, למי צלצל הפעמון?, באתר "נסיכת המדעים"
• יוסי לוי, ההיסטוריה של ההתפלגות הנורמלית, באתר "נסיכת המדעים"
• 
  שגיאות פרמטריות בתבנית:בריטניקה
  פרמטרי חובה [ 1 ] חסרים
• התפלגות נורמלית, באתר MathWorld (באנגלית)   

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32648929התפלגות נורמלית